1. Постановка задачи для конкретного варианта и исходные данные:
Найти корень уравнения e- x - x =0 на отрезке [0, 1] с точностью e=0,0001 при помощи методов половинного деления, хорд, касательных и простой итерации, используя программирование ячеек рабочего листа. Имеем: f (x)= e- x - x, a=0, b=1, e=0,0001.
2. Доказательство того, что внутри отрезка [0, 1] существует единственный корень уравнения e- x - x =0.
Доказательство этого факта проведите и оформите самостоятельно. (При доказательстве можно использовать любой из пунктов 2, 3 или 4 лабораторной работы №1.)
3. Описание метода решения нелинейного уравнения с анализом сходимости итерационного процесса, его блок-схема и зарисовка фрагмента рабочего листа с указанием формул, которые необходимо ввести для каждого из соответствующих численных методов.
а) метод половинного деления
Описание метода см. в п. 2.1 (для конкретного варианта дать описание метода самостоятельно).
Блок схема метода половинного деления представлена в прил.1
(см. с.52).
Фрагмент рабочего листа с указанием формул или значений, которые
необходимо ввести для метода половинного деления:
| Ячейка | Формула либо значение |
| A1 B1 C1 D1 E1 F1 A2 B2 C2 D2 E2 F2 G2 A3 B3 C3 | n а b xn f(a) f(xn) =(B2+C2)/2 =EXP(-B2)-B2 =EXP(-D2)-D2 =ЕСЛИ(C2-B2<0,0001;"стоп";"далее") =A2+1 =ЕСЛИ(E2*F2<0;B2;D2) =ЕСЛИ(E2*F2<0;D2;C2) |
Далее, выделив диапазон D2:G2, расположите указатель мыши на маркере заполнения и пробуксируйте его на одну строку ниже (см. рис. ниже).
И окончательно, выделив диапазон A3:G3, расположить указатель мыши на маркере заполнения и пробуксировать его вниз (см. рис. ниже) до тех пор, пока в столбце G не появится сообщение «стоп», что означает что корень найден и его значение находится в столбце D.
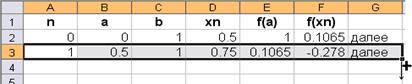
В данном случае это сообщение появится в ячейке G16, а значение корня с точностью 0,0001 равно 0,5672 и находится в ячейке D16. Ниже приведен фрагмент рабочего листа и результат нахождения корня с точностью 0,0001 методом деления пополам уравнения e- x - x =0.
б) метод хорд
Описание метода см. в п. 2.2 (для конкретного варианта дать описание метода самостоятельно).
Поскольку f (0)=1 и 
, а значит 
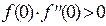, то согласно правилу (см.с.14), по которому определяется тот конец отрезка, который будет неподвижен, и выбор формулы, имеем:
Блок схема метода хорд представлена в прил.2 (см. с.53).
Фрагмент рабочего листа с указанием формул или значений, которые необходимо ввести для метода хорд:
| Ячейка | Формула либо значение |
| A1 B1 C1 D1 E1 A2 B2 C2 D2 E2 A3 B3 F3 | n xn f(xn) a f(a) =EXP(-B2)-B2 =EXP(-D2)-D2 =A2+1 =B2-(B2-$D$2)*C2/(C2-$E$2) =ЕСЛИ(ABS(B3-B2)<0,0001;"стоп";"далее") |
Далее, выделив ячейку С2, расположите указатель мыши на маркере заполнения и пробуксируйте его на одну строку ниже (см. рис. ниже).
И окончательно, выделив диапазон A3:F3, расположить указатель мыши на маркере заполнения и пробуксировать его вниз (см. рис. ниже) до тех пор, пока в столбце F не появится сообщение «стоп», что означает, что корень найден.
В данном случае сообщение появится в ячейке F7, а значение корня с точностью 0,0001 равно 0,5672 и находится в ячейке В7. Ниже приведены фрагмент рабочего листа и результат нахождения корня с точностью 0,0001 методом хорд уравнения e- x - x =0.
в) метод касательных
Описание метода см. в п. 2.3. (Для конкретного варианта дать описание метода самостоятельно.)
Для обоснования сходимости метода касательных проверим выполнение условия (7) на концах отрезка [0,1]. Поскольку, f ’’(x)>0, " x Î[0,1], а f (0)=1>0, f (1)= -0,63212<0, то f (0) f ’’(x)>0, x Î[0,1] и в качестве начального приближения x 0 следует взять x 0=0. Формула для вычисления первого шага итерационного процесса выглядит следующим образом:
Блок схема метода касательных представлена в прил.3.
Фрагмент рабочего листа с указанием формул или значений, которые необходимо ввести для метода касательных:
| Ячейка | Формула либо значение |
| A1 B1 C1 D1 A2 B2 C2 D2 A3 B3 E3 | n xn f(xn) f’(xn) =EXP(-B2)-B2 =-EXP(-B2)-1 =A2+1 =B2-C2/D2 =ЕСЛИ(ABS(B3-B2)<0,0001;"стоп";"далее") |
Далее, выделив диапазон C2:D2, расположите указатель мыши на маркере заполнения и пробуксируйте его на одну строку ниже (см. рис. ниже).
И окончательно, выделив диапазон A3:E3, расположить указатель мыши на маркере заполнения и пробуксировать его вниз (см. рис. ниже) до тех пор, пока в столбце E не появится сообщение «стоп», что означает, что корень найден.
В данном случае сообщение появится в ячейке E6, а значение корня с точностью 0,0001 равно 0,5671 и находится в ячейке В6. Ниже приведены фрагмент рабочего листа и результат нахождения корня с точностью 0,0001 методом касательных уравнения e- x - x =0.
г) метод простой итерации
Описание метода см. в п. 2.4 (для конкретного варианта дать описание метода самостоятельно).
Данное уравнение (e- x - x =0) приведем к виду (8):
x = e- x или x= j(x), где j(x)= e- x.
Так как j’(x)= - e- x, |j’(x)|=| e- x |<1, " x Î(0,1] то условие (10) выполнено; процесс итераций будет сходиться. Взяв в качестве начального приближения середину отрезка, т.е. 
, вычисления последующих приближений проведем по формуле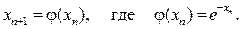 
Блок схема метода простой итерации представлена в прил.4 (см. с.54).
Фрагмент рабочего листа с указанием формул или значений, которые необходимо ввести для метода простой итерации:
| Ячейка | Формула либо значение |
| A1 B1 C1 A2 B2 C2 A3 B3 D3 | n xn j(xn) 0,5 =EXP(-B2) =A2+1 =C2 =ЕСЛИ(ABS(B2-B3)<0,0001;"стоп";"далее") |
Далее, выделив ячейку C2, расположите указатель мыши на маркере заполнения и пробуксируйте его на одну строку ниже (см. рис. ниже).
И окончательно, выделив диапазон A3:D3, расположите указатель мыши на маркере заполнения и пробуксируйте его вниз (см. рис. ниже) до тех пор, пока в столбце D не появится сообщение «стоп», что означает, что корень найден.
В данном случае сообщение появится в ячейке D16, а значение корня с
|
| Решение уравнения e- x - x =0 | Название численного метода | |||
| метод половинного деления | метод хорд | метод касательных | метод простой итерации | |
| Вычисленное значение корня | 0,5672 | 0,5672 | 0,5671 | 0,5671 |
| Число итераций |
4. Результаты работы для каждого из указанных численных методов выписать в следующем виде (вывод итоговой оценки для корня должно быть выведено лишь с верными цифрами (число верных цифр после десятичной точки имеет порядок Lg(1/e)):
5. Полученные результаты проанализировать самостоятельно.
