Введение
Рассматривается решение нелинейного уравнения
| f (x)=0. | (1) |
Ясно, что любое нелинейное уравнение можно свести к виду (1).
Определение 1. Корнем уравнения (1) называется такое значение x = v аргумента, при котором это уравнение обращается в тождество, т.е. f (v)=0.
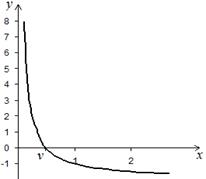
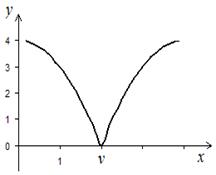
Корни уравнения (1) могут быть действительными и комплексными. В дальнейшем будет идти речь только о вычислении действительных корней. Геометрически корень уравнения (1) представляет собой абсциссу точки пересечения, точки касания или другой общей точки графика функции y = f (x) и оси O x (рис. 1).

a) б) в)
Рис. 1. x = v – корень уравнения f (x)=0:
а) x = v – абсцисса точки пересечения графика функции y = f (x) и оси O x;
б) x = v – абсцисса точки касания графика функции y = f (x) и оси O x;
в) x = v – иной случай
Определение 2. Если функция f (x) имеет вид многочлена, то уравнение (1) называется алгебраическим.
Линейное, квадратное и биквадратное уравнения являются примерами алгебраических уравнений.
Приведём некоторые свойства алгебраических уравнений:
1. Всякое алгебраическое уравнение имеет по крайней мере один корень (действительный или комплексный).
2. Всякое алгебраическое уравнение n -й степени имеет не более n корней.
3. Всякое алгебраическое уравнение с действительными коэффициентами может иметь лишь четное число комплексных корней.
4. Всякое алгебраическое уравнение нечётной степени с действительными коэффициентами имеет по крайней мере один действительный корень.
Определение 3. Если f (x) включает в себя тригонометрические или экспоненциальные функции, то (1) называется трансцендентным, например x lg x = 1 или cos x = x 3.
Решение квадратных и биквадратных уравнений, наипростейших тригонометрических и степенных, известно. Для кубических уравнений вводятся формулы Кардано. В общем же случае надежд на простое аналитическое решение нет. Более того, доказано, что даже алгебраическое уравнение выше четвертой степени неразрешимо в элементарных функциях. Итак, не всякое уравнение может быть решено точно. Однако в прикладных задачах это не является необходимым. К примеру, при изготовлении деталей многих точных механизмов допустимое отклонение от нормы измеряется тысячными долями миллиметра, или при измерении диаметра трубы газопровода допускается погрешность до 1 мм. Задачу отыскания корней можно считать практически решенной, если мы сумеем определить корни с заданной точностью e.
В общем виде задача заключается в следующем:
Во-первых, установить, имеет ли уравнение (1) действительные корни, и если имеет, то сколько. Во-вторых, определить значение действительного корня уравнения (1) или точно (если это возможно и если имеет смысл), или с погрешностью, не превосходящей заданного, достаточно малого e>0. Иными словами, если v Î[a,b] - истинное значение корня уравнения (1), т.е. f (v)=0, то требуется определить такое число x *, что | x *- v |<e.
Методы решения нелинейных уравнений делятся на прямые и итерационные. Первые позволяют найти решение непосредственно с помощью формул и всегда обеспечивают получение точного решения x=v (примером такого рода является формула корней квадратного уравнения). В итерационных методах процедура решения задается в виде многократного применения некоторого алгоритма. Полученное решение x * всегда является приближенным, хотя может быть сколь угодно близким к точному решению v. Итерационные методы наиболее универсальны и удобны для реализации на ЭВМ.
Основными, наиболее употребляемыми, итерационными методами решения нелинейных уравнений являются: 1) метод половинного деления (дихотомии);
2) метод хорд (метод секущих); 3) метод касательных (метод Ньютона); 4) метод простых итераций.
Алгоритм реализации любого итерационного метода состоит из двух частей:
1) отделение корней – отыскание некоторого приближенного значения корня или содержащего его отрезка (при этом выделяются области, содержащие только один корень, и рассматривается вопрос о кратности корней);
2) уточнение корня – построение итерационного процесса, позволяющего уточнить значение корня.
Что касается отделения корней, тут нет формальных методов, отрезки определяются или табуляцией, или исходя из физического смысла, или аналитическими методами. Уточнение корня выполняется различными итерационными методами, суть которых в последовательном уточнении начального приближения корня x 0 – x 1, x 2, …, xn. Если значение xi, i =1,2, … с ростом n приближается к истинному значению корня v, то процесс сходится. Выходом из итерационного процесса являются условия: | f (xn)|< e и | xn - xn- 1 |< e. Всюду далее будем предполагать достаточным выполнения одного из этих условий. Это означает, что все функции в следующих далее лабораторных работах являются не слишком «крутыми» и не слишком «пологими» вблизи истинного корня.
Отделение корней
Часто при решении уравнения важно знать заранее, имеет ли оно корни, и если имеет, то где они, примерно, располагаются. В общем случае отделение корней уравнения (1) базируется на известной теореме о существовании корня непрерывной функции из математического анализа:
Теорема (о существовании корня непрерывной функции). Если функция f (x) непрерывна на отрезке [a,b] и принимает на его концах значения разных знаков, то на этом отрезке существует по крайней мере один корень уравнения (1).
Определение непрерывной функции и некоторые свойства рассматриваются и доказываются в [5] (лекция 4, с.15).
Коротко прокомментируем эту теорему. Во-первых, требование непрерывности функции f (x) во всех точках отрезка [a,b] существенно. При наличии хотя бы одной точки разрыва утверждение теоремы становится неверным. Для примера рассмотрим график функции  (рис. 2). Здесь, мы имеем график разрывной функции, которая принимает на концах отрезка [0,1] значения разных знаков (f (0)=-2<0; f (1)=3>0), но не имеющей корней.
(рис. 2). Здесь, мы имеем график разрывной функции, которая принимает на концах отрезка [0,1] значения разных знаков (f (0)=-2<0; f (1)=3>0), но не имеющей корней.
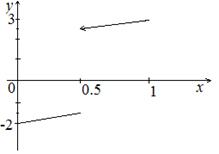
Рис. 2. Пример разрывной функции, принимающей на отрезке [0,1]
значения разных знаков, но не имеющей на этом отрезке корней
Во-вторых, гарантируя существование решения уравнения (1), теорема не позволяет определить число его корней. К примеру, рассмотрев функцию
f (x) = sin8 x - 0,5 (её график приведен на рис.3), видно, что она непрерывна на всей числовой оси, на концах, скажем отрезка [1,2], принимает значения разных знаков – имеет на этом отрезке, три корня.

Рис. 3. Пример функции f (x)=sin8 x -0,5, имеющей на отрезке [1,2] три корня
Иногда число корней можно установить с помощью дополнительных исследований. А именно, приведем следующие следствия из теоремы о существовании корня непрерывной функции:
Следствие 1. Если функция f (x) непрерывна на отрезке [a,b], принимает на его концах значения разных знаков и монотонно возрастает (убывает), то на этом отрезке существует единственный корень уравнения (1).
Необходимым и достаточным признаком монотонности функции f (x) на отрезке является сохранение знака её производной (см.[5], теорема 16, c.31). Поэтому естественно следующее следствие:
Следствие 2. Если функция f (x) непрерывна на отрезке [a,b], дифференцируема внутри [a,b], принимает на его концах значения разных знаков и f’ (x)>0 (f’ (x)<0) внутри [a,b], то на отрезке [a,b] существует единственный корень уравнения (1).
Рассмотрим в качестве примера функцию f (x) =x-ex-2, график которой приведён на рис.4. Эта функция непрерывна на [0,1], дифференцируема внутри [0,1],
f (0) = - e -2= -0,13534<0, f (1)=1- e -1= 0,632121>0. Производная этой функции имеет вид: f’ (x)=1 - ex-2. В интересующей нас области изменения переменной x Î[0,1] производная положительна. Следовательно, функция f (x) =x-ex-2 на отрезке [0,1] монотонно возрастает и может иметь только один корень.
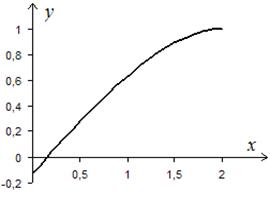
Рис. 4. Пример функции f (x) =x-ex-2, непрерывной на отрезке [0,1],
принимающей на концах отрезка значения разных знаков и
монотонно возрастающей на этом отрезке
Заметим, что сохранение знака второй производной функции f (x) на отрезке (при прочих условиях), также будет означать существование единственного корня f (x) на этом отрезке. А именно, справедливо следующее следствие:
Следствие 3. Если функция f (x) непрерывна на отрезке [a,b], дважды дифференцируема внутри [a,b], принимает на его концах значения разных знаков и
f ’’ (x)>0 (f ’’ (x)<0) внутри [a,b], то на отрезке [a,b] существует единственный корень уравнения (1).
В общем случае выбирают некоторый диапазон, где могут обнаружиться корни, и осуществляют "прогулку" по этому диапазону с выбранным шагом h (обычно выбирают в качестве h единицу) для обнаружения перемены знаков f (x), т.е. f (x)× f (x+h) < 0.
Следует заметить, что иногда удается выяснить картину расположения корней уравнения (1) с помощью эскиза графика функции f (x). То есть, отделение корней уравнения (1) можно выполнить графически, построив график функции f (x), по которому можно судить о том, в каких промежутках находятся точки пересечения его с осью О х. В некоторых случаях целесообразно представить уравнение (1) в эквивалентном виде
| f 1(x)= f 2(x) | (2) |
с таким расчетом, чтобы графики функций y = f 1(x) и y = f 2(x) строились проще, чем график f (x). Корень уравнения (2) представляет собой абсциссу точки пересечения графиков y = f 1(x), y = f 2(x).
Лабораторная работа № 1 на тему: «Отделение корней
нелинейного уравнения аналитически и графически»
Цель работы:
Изучить процедуру отделения корней.
Постановка задачи:
Для нелинейного уравнения
1) отделить корни аналитически;
2) отделить корни графически.
3) протабулировав исходное уравнение и его производную в табличном процессоре MS Excel, убедиться в наличии или отсутствии корней внутри найденного вами отрезка.
Содержание отчета:
1. Постановка задачи для конкретного варианта и исходные данные.
2. Теоретическое описание аналитического отделения корней и нахождение промежутков, содержащих искомые корни.
3. График данной функции. Вывод – промежутки, содержащие корни.
4. Табулирование заданной функции и её производной в табличном процессоре MS Excel. Вывод – о наличии или отсутствии корней внутри найденного вами промежутка. Сравнение с результатами, найденными в п.2, 3.
Варианты заданий приведены в табл.1 (см.с.10).
образец выполнения лабораторной работы №1
1. Постановка задачи для конкретного варианта и исходные данные
Для нелинейного уравнения 3 x -2 x -4=0
1) отделить корни аналитически;
2) отделить корни графически;
3) протабулировать заданную функцию и её производную в табличном процессоре MS Excel.
2. Теоретическое описание аналитического отделения корней
Обозначим f (x)=3 x -2 x -4. Данная функция определена, непрерывна и дифференцируема на всей числовой оси, т.е. для x Î(-¥,¥). Разобьём всю область допустимых значений на промежутки, в каждом из которых содержится только один корень или не содержится ни одного. Поскольку все точки экстремума (точки максимума или минимума) функции находятся в множестве ее критических точек, то находим производную f’ (x)= 3 x ln3-2. Вычислим корень производной: 3 x ln3-2=0; 3 x =  ; lg3 x =lg
; lg3 x =lg  ; x lg3=lg2-lg(ln3); x =
; x lg3=lg2-lg(ln3); x = 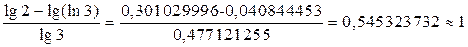 .
.
Заметим, что данная функция убывает на (-¥,1) (f’ (x)<0 для x Î(-¥,1)) и возрастает на (1, +¥) (f’ (x)>0 для x Î(1, +¥)).
Составим таблицу знаков функции f (x) (Sgn f (x)), полагая x равным:
a) критическим значениям функции (корням производной) или близким к ним;
b) граничным значениям (исходя из области допустимых значений неизвестного):
| x | -¥ | +¥ | |
| Sgn f (x) | + | - | + |
f (-100)=3-100-2(-100)-4>0; f (1)=31-2×1-4<0; f (100)= 3100-2×100-4>0.
Так как происходит две перемены знака функции, то уравнение имеет два действительных корня. Чтобы завершить операцию отделения корней, следует уменьшить промежутки, содержащие корни, так чтобы их длина была не больше 1. Для этого составим новую таблицу знаков функции f (x):
| x | -2 | -1 | |||
| Sgn f (x) | + | - | - | - | + |
f (-2)= 3-2-2×(-2)-4=0,111111>0; f (-1)=3-1-2(-1)-4=-1,66667<0;
f (0)=30-2×0-4=-3<0; f (2)= 32-2×2-4=1>0.
Таким образом, аналитическое отделение корней показывает, что корни заключены в следующих промежутках: x 1Î[-2,-1], x 2Î[1,2].
3. График данной функции.
Для построения графика функции f (x)=3 x -2 x -4 можно использовать либо табличный процессор MS Excel, либо любой другой способ. График заданной функции будет выглядеть следующим образом:

Можно было переписать уравнение 3 x -2 x -4=0 в эквивалентном виде 3 x =2 x +4 и построить графики функций y =3 x, y =2 x +4:

В любом случае, корни уравнения y = f (x) это абсциссы точек пересечения графика y = f (x) с осью О х, либо абсциссы, в которых графики функций y 1 и y 2 пересекаются.
Из графиков видно, что уравнение имеет два корня: x 1Î[-2,-1], x 2Î[1,2].
4. Табулирование заданной функции и её производной в табличном процессоре MS Excel. Вывод - наличие или отсутствие корней внутри найденного вами промежутка.
Найдем значения функции f (x)=3 x -2 x -4 и её производной f’ (x)= 3 x ln3-2 при различных значениях аргумента, меняющегося с фиксированным шагом. Шаг выбирают небольшим, так чтобы таблица значений функции отражала её поведение на интервале табуляции. В нашем случае возьмем в качестве шага изменения аргумента, например, 0,5. Из п.2 и 3 настоящей лабораторной работы (см. выше) нам известно, что корни уравнения 3 x -2 x -4=0 находятся в промежутках [-2,-1] и [1,2]. Поэтому протабулируем x от -2,5 до 2,5 с шагом 0,5. Отметим, что эта последовательность значений представляет собой арифметическую прогрессию. Предположим, что заголовки таблицы x, f (x) и f’ (x) записаны в ячейках A1, B1 и С1 соответственно. Ввести в ячейки диапазона ряд последовательных значений, образующих арифметическую прогрессию, можно двумя способами.
Первый способ: · В ячейки А2 и А3 введите первый и второй члены арифметической прогрессии. В данном случае это -2,5 и -2 соответственно.
· Выделите диапазон ячеек А2:А3.
· Расположите указатель мыши на маркере заполнения выделенного диапазона и протяните его вниз (в данном случае на диапазон А4:А12) до тех пор, пока не получится числовой ряд нужной длины.
Второй способ: · В ячейку А2 введите первый член арифметической прогрессии.
· Выберите команду меню Правка / Заполнить / Прогрессия.
· В появившемся диалоговом окне Прогрессия в группе Расположение выбираем переключатель по столбцам, а в группе Тип – переключатель арифметическая. В поле Шаг введите значение 0,5, а в поле Предельное значение – 2,5.
· Нажмите кнопку ОК.
· Диалоговое окно Прогрессия закроется, а на рабочем листе автоматически будет построена требуемая прогрессия.
Далее, в ячейку В2 введите формулу исходной функции: =3^A2-2*A2-4, а в ячейку С2 формулу её производной: =3^A2*LN(3)-2. Выделив диапазон ячеек В2:С2, расположите указатель мыши на маркере заполнения выделенного диапазона и протяните его вниз на диапазон В3:С12. Процесс создания таблицы значений функции завершен (рис.5).

Рис. 5. Результат табуляции функции f (x)=3 x -2 x -4 и её производной
Проанализируем полученный результат табуляции функции f (x)=3 x -2 x -4.
Из рис.5 видно, что значения функции f (-2) = 0,11111>0, f (-1)=-1,666<0 и f’ (x)<0 для всех x из [-2,-1]. Согласно следствию 2 (см. с. 6), делаем вывод, что на [-2,-1] существует единственный корень.
Аналогично рассуждая применительно к отрезку [1,2], получим, что на этом отрезке существует ещё один корень данного уравнения.
Полученные значения совпадают с результатами, найденными в пунктах 2, 3.
Таблица 1
ВАРИАНТЫ ЗАДАНИЙ для лабораторной работы №1
| № вар. | Уравнение | № вар. | Уравнение |
| 3 x -1-4- x =0; | 2lg x -  +1=0; +1=0;
| ||
| 2 x -lg x -7=0; | e x + x +1=0; | ||
| 2e x =5 x -2; | Sin(x +1)=0,5 x; | ||
| x 4- x -1=0; | x 3-6 x =8; | ||
| 5sin x = x -1; | 3 x +2 x -3=0; | ||
| 2arctg x -3 x +2=0; | arctg(x -1)+2 x =0; | ||
| 2 x 4- x 2-10=0; | 3 x -2 x +5=0; | ||
| 2 x -3 x -2=0; | 3 x 4+4 x 3-12 x 2-5=0; | ||
| x 22 x =3; | arctg x -  =0; =0;
| ||
| x 3-3 x 2+9 x -8=0; | x lg x -1,2=0. |
2. Уточнение корней нелинейного уравнения при помощи некоторых
численных методов






