Выборочные числовые характеристики. Мы наблюдаем случайный вектор (X, Y), имеющий нормальное распределение:

Мы наблюдаем случайный вектор (X, Y), имеющий нормальное распределение: . Требуется получить выборку этого вектора из n = 425 элементов, и затем найти его выборочные числовые характеристики.

Смоделируем случайный вектор. Вектор

можно смоделировать с помощью стандартной функции grand. Тогда искомый вектор получится преобразованием:

Пусть теперь у нас имеется выборка . Требуется отыскать выборочные числовые характеристики.

Математическим ожиданиям соответствуют выборочные средние:

Дисперсиям соответствуют выборочные дисперсии:

Также можно отыскать выборочный коэффициент корреляции:

В нашем случае получаем:

0.1437882

- 3.6484266

11.680413

3.5600119

=0.5259053

Отклонения выборочных характеристик от действительных:

0.1062118

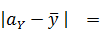0.0515734

0.9804133

1.4399881

0.0659053

Гипотеза о независимости

Пусть у нас имеется выборка случайного вектора (X, Y). Требуется проверить гипотезу о независимости случайных величин X и Y.

Сначала воспользуемся критерием χ². Разобьем выборочные значения на одинаковые интервалы группировки, после чего объединим некоторые из них так, чтобы в каждый интервал группировки попало не менее 5 точек.

В результате получились следующие одномерные таблицы частот.

Номер интервала
	[-9.6565917; -0.0531472)	0.4715789
	[-0.0531472; 1.8675417)	0.2315789
	[1.8675417; 3.7882306)	0.1621053
	[3.7882306; 9.550273)	0.1347368

Номер интервала
	[-9.2029762; -3.7562468)	0.4673684
	[-3.7562468; -2.6669009)	0.2442105
	[-2.6669009; 1.6904826)	0.2884211

Обозначения в этих двух таблицах аналогичны обозначениям в пункте 2.1.1.

Построим также двумерную таблицу частот. В ней по вертикали расположим интервалы первой координаты вектора, а по горизонтали – второй.

Номер интервала

Затем вычисляем статистику χ² по следующей формуле:

где K, L – число получившихся интервалов группировки для X и Y соответственно;
ν – двумерная частота группировки;
ν^X, ν^Y – одномерные частоты группировки для X и Y соответственно.

В нашем случае 84.445194

Теперь зададим порог , который представляет собой (1-α)-квантиль распределения .

Получаем, 43.082788

Статистика превышает порог, значит, гипотезу о независимости величин X и Y следует отвергнуть.

Теперь проверим ту же гипотезу с помощью критерия значимости корреляции.

Статистика этого критерия:

, где – выборочный коэффициент корреляции.

Получаем, T = 13.447507

Порогом данной статистики является , т.е. -квантиль распределения Стьюдента с числом степеней свободы (n-2), который для заданных данных равен =2.576

Статистика снова превышает порог, следовательно, гипотезу о независимости случайных величин X и Y и по этому критерию следует отвергнуть.

Уравнения регрессии

Имея выборку случайного вектора (X, Y), распределённого по нормальному закону с неизвестными параметрами, требуется построить эмпирические уравнения регрессии величины X на Y и Y на X.

Уравнениями регрессии случайной величины Y на случайную величину X и X на Y соответственно называются уравнения:

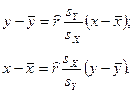
Построим геометрическое место точек, удовлетворяющих этим уравнениям, а также точки из выборки .

Надо сказать, что чем ближе к единице будет по абсолютной величине коэффициент корреляции, тем теснее будут расположены точки относительно прямой регрессии и, наоборот, чем ближе к нулю коэффициент корреляции, тем более расплывчато точки будет располагаться относительно прямой.

ЗАКЛЮЧЕНИЕ

В заключении сделаем выводы об изменении качества всех статистических выводов при увеличении объема выборки n, качества построения доверительных интервалов в зависимости от доверительной вероятности γ, качества проверки гипотез в зависимости от уровня значимости α.

При увеличении объема выборки значения выборочных характеристик (выборочное среднее, выборочная дисперсия и т.д.) приближаются к истинными значениями. То есть при увеличении выборки можно получить большую точность оценок.

Если увеличить доверительную вероятность γ, то границы доверительного интервала станут шире, т.е. возрастет вероятность, с которой интервал «накрывает» истинное значение неизвестного параметра.

Уровень значимости α определяет уровень ошибки первого рода (когда гипотеза верна, но она опровергается). Но если мы уменьшаем уровень значимости, стараясь свести вероятность опровергнуть гипотезу к минимальной, то будет увеличиваться вероятность ошибки второго рода (когда гипотеза неверна, но она принимается). Поэтому чаще всего используют уровни значимости 0,05 и 0,01, так как они обеспечивают компромисс между ошибками первого и второго рода

Список литературы

1. Коломиец Э.И. Математическая статистика: Метод. указания к решению задач/ Куйбышев. авиац. ин-т. Куйбышев, 1990.

2. Суханов С.В. Дипломная работа. Оформление пояснительной записки: Метод. указания / Самарский гос. аэрокосм. ун-т. Самара, 1999.

3. Ермаков С.М., Михайлов Г.А. Статистическое моделирование. М.: «Наука», 1982.

4. Харин Ю.С., Степанова М.Д. Практикум на ЭВМ по математической статистике. Минск: Изд-во «Университетское», 1987.

5. Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере /Под ред. Фигурнова В.Э. М.: «ИНФРА-М», 1998.

ПРИЛОЖЕНИЕ Б. Задание №1

function [ x ]= model1 ()

n=475;

a=0.25;

sigma=10.7;

alpha=0.001;

gamma=0.999;

for i=1:1:n

s=0;

for j=1:1:12

s=s+rand();

end

x (i)=((sigma^(1/2))*(s-6))+a;

end

endfunction

function [ y ]= f (x) // Нормальный закон распределения N(a,d)

n=475;

a=0.25;

sigma=10.7;

alpha=0.001;

gamma=0.999;

y = (1/sqrt(2*%pi*sigma)) * exp(-(x -a)^2 / (2*sigma));

endfunction

function [ k, u, nu ]= drawHistogram (x) // Построение графиков

n=475;

a=0.25;

sigma=10.7;

alpha=0.001;

gamma=0.999;

k = floor(1 + 3.32* log10 (n)) + 1; // Число интервалов

u = zeros(1, k +1); // Границы интервалов

nu = zeros(1, k); // Частоты интервалов

// Вычисление границ интервалов

u (1) = min(x);

u (k +1) = max(x);

du = (u (k +1) - u (1)) / k;

for i = 2: k,

u (i) = u (i-1) + du;

end;

disp(du);

// Вычисление частот интервалов

for i = 1: n,

for j = 1: k -1,

if u (j)<= x (i) & x (i)< u (j+1),

nu (j) = nu (j)+1;

break;

end;

if u (k)<= x (i) & x (i)<= u (k +1),

nu (k) = nu (k)+1;

end;

h = zeros(1, k +2); // Высоты

p = zeros(1, k); // Относительные частоты интервалов

uu = zeros(1, k +2); // Центры интервалов

// Вычисление высот, отн. частот инте-лов и центров инт-лов

h(1) = 0;

h(k +2) = 0;

uu(1) = u (1) - du/2;

uu(k +2) = u (k +1) + du/2;

for i = 1: k,

p(i) = nu (i) / n;

uu(i+1) = (u (i) + u (i+1)) / 2;

h(i+1) = p(i) / du;

end;

disp(u,'Границы интервалов');

disp(nu,'Частоты интервалов');

disp(p,'Относительные частоты интервалов');

disp(sum(nu),'Сумма частот');

disp(sum(p),'Сумма относительных частот');

disp(h(2: k +1),'Высоты столбцов гистограммы');

disp(f (uu(2: k +1)),..

'Теоретическая плотность в серединах инт-лов');

// построение графиков

histplot (k, x, style=2, rect=[ u (1)-du, 0, u (k +1)+du, max(h)+0.02]);

// гистограмма

x = [ u (1)-du: 0.0001: u (k +1)+du]; // Значение Х

//для теоретической плотности вероятностей (голубой)

plot2d(uu, h, 1); // Полигон частот (черный)

plot2d(x, f (x), 5); // Теоретическая плотность вероятностей (красный)

endfunction

//x=model1();

//[k,u,nu]=drawHistogram(x);

//disp('Графики построены!');

function [ M, D ]= dispersion1 (x)

//выборочное среднее и выборочная дисперсия

n=475;

a=0.25;

sigma=10.7;

alpha=0.001;

gamma=0.999;

v=0;

for i=1:1:n

v=v+ x (i);

end

M =v/n;

k=0;

for i=1:1:n

k=k+(x (i))^2;

end

k=k/n;

D =k- M ^2;

endfunction

function []= dispersion2 (x)

n=475;

a=0.25;

sigma=10.7;

alpha=0.001;

gamma=0.999;

[M,D]= dispersion1 (x);

sM=abs(a-M);

disp(sM,'|MX-teta1|')

sD=abs(sigma-D);

disp(sD, '|DX - teta2|');

ss2=n/(n-1)*D;

disp(M, 'Несмещенная оценка мат.ожидания');

disp(ss2, 'Несмещенная оценка дисперсии');

disp(abs(sigma-ss2), '|DX - s`^2|');

endfunction

function []= dispersion3 (x)

//доверительные границы

n=475;

a=0.25;

sigma=10.7;

alpha=0.001;

gamma=0.999;

[M,D]= dispersion1 (x);

interv1=(n*D)/(((3.291+sqrt(2*n-1))^2)/2)

interv2=(n*D)/(((-3.291+sqrt(2*n-1))^2)/2)

interv3=M-(3.291*(sqrt(D)/sqrt(n-1)))

interv4=M+(3.291*(sqrt(D)/sqrt(n-1)))

printf ('доверительный интервал для дисперсии (');

printf ('%f',interv1);

printf (' ');

printf ('%f',interv2);

printf (')\n');

printf ('доверительный интервал для мат.ожидания (');

printf ('%f',interv3);

printf (' ');

printf ('%f',interv4);

printf (')');

disp(M,'Мат.ожидание');

disp(D,'дисперсия');

endfunction

function []= stat (x)

n=475;

a=0.25;

sigma=10.7;

alpha=0.001;

gamma=0.999;

k = floor(1 + 3.32* log10 (n)) + 1; // Число интервалов

_u = zeros(1,k+1); // Границы интервалов

_nu = zeros(1,k); // Частоты интервалов

u = zeros(1,k+1); // Границы интервалов

nu = zeros(1,k); // Частоты интервалов

// Вычисление границ интервалов

u(1) = min(x);

u(k+1) = max(x);

du = (u(k+1) - u(1)) / k;

for i = 2: k,

u(i) = u(i-1) + du;

end;

// Вычисление частот интервалов

for i = 1: n,

for j = 1: k-1,

if u(j)<= x (i) & x (i)<u(j+1),

nu(j) = nu(j)+1;

break;

end;

if u(k)<= x (i) & x (i)<=u(k+1),

nu(k) = nu(k)+1;

end;

// вычисление новых интервалов и частот

_u(1) = u(1);

i = 0; // Счетчик старых значений

j = 0; // Счетчик новых значений

while i<k,

j = j + 1;

while (_nu(j)<5 & i<k),

i = i + 1;

_nu(j) = _nu(j) + nu(i);

end;

_u(j+1)=u(i+1);

if (i==k & _nu(j)<5),

_nu(j-1)=_nu(j-1)+_nu(j);

_u(j) = _u(j+1);

_nu(j) = 0;

_u(j+1) = 0;

j = j - 1;

end;

old_p = zeros(1,k); // Старая теоретическая вероятность

for i = 1: k,

old_p(i) = cdfnor("PQ", u(i+1), a, sqrt(sigma)) -..

cdfnor("PQ", u(i), a, sqrt(sigma));

end;

//disp(u,'Границы старых интервалов');

//disp(old_p,'Теоретические вероятности старых интервалов');

N = j; //disp(N, 'Новое число интервалов');

_u = _u(1:N+1); //disp(_u, 'Новые границы интервалов');

_nu = _nu(1:N); //disp(_nu, 'Новые частоты интервалов');

_p = _nu / n; //disp(_p, 'Новые относительные частоты интервалов');

// Теоретическая вероятность

[M,D]= dispersion1 (x);

p = zeros(1,N); // Параметры известны

pp = zeros(1,N); // Параметры неизвестны

for i = 1: N,

p(i) = cdfnor("PQ", _u(i+1), a, sqrt(sigma)) -..

cdfnor("PQ", _u(i), a, sqrt(sigma));

pp(i) = cdfnor("PQ", _u(i+1), M, sqrt(D)) -..

cdfnor("PQ", _u(i), M, sqrt(D));

end;

//disp(p, 'Теоретические вероятности новых интервалов');

//disp(pp, 'Теоретические вероятности новых интервалов (параметры неизвестны)');

//disp(sum(_nu),'Сумма новых частот');

//disp(sum(_p),'Сумма новых относительных частот');

function [ ans ]= stat (N, u, p) // Статистика критерия hi^2

ans = 0;

for i = 1: N,

ans = ans + (_nu(i)-n* p (i))^2 / (n* p (i));

end

endfunction

hi_2_alpha_0_99 =.. // Распределение hi^2..

.. // alpha = 0.99; n <= 10..

[ 6.635, 9.210, 11.345, 13.277, 15.086,..

16.812, 18.475, 20.090, 21.666, 23.209]';

h = hi_2_alpha_0_99(N - 1); // ïîðîã

r = 2; // Число неизвестных параметров

hh = hi_2_alpha_0_99(N - 1 - r);

t = stat (N,_u,p);

if t >= h,

disp([t,h],..

'Параметры известны: гипотеза отвержена (t >= h)');

else

disp([t,h],..

'Параметры известны: гипотеза принята (t < h)');

end;

tt = stat (N,_u,pp);

if tt >= hh,

disp([tt,hh],..

'Параметры неизвестны: гипотеза отвержена (t >= h)');

else

disp([tt,hh],..

'Параметры неизвестны: гипотеза принята (t < h)');

end;

endfunction

ПРИЛОЖЕНИЕ Б. Задание №2

function [ x ]= model2 ()

a=2;

b=-4;

alpha=0.05;

n=400;

gamma=0.95;

for i=1:1:n

U=rand();

if (U<0.5) then x (i)=(((b-a)*U)/b)^(1/a);

else x (i)=(((b-a)*(U-1))/a)^(1/b);

end

endfunction

function [ y ]= ff (x)

a=2;

b=-4;

alpha=0.05;

n=400;

gamma=0.95;

if ((x >=0)&(x <1)) then y =(a*b* x ^(a-1))/(b-a);

else

if (1<= x) then y =((a*b)* x ^(b-1))/(b-a);

else y =0;

end

endfunction

function []= drawHistogram2 (x) // Построение графиков

a=2;

b=-4;

alpha=0.05;

n=400;

gamma=0.95;

k = floor(1 + 3.32* log10 (n)) + 1; // Число интервалов

u = zeros(1,k+1); // Границы интервалов

nu = zeros(1,k); // Частоты интервалов

// Вычисление границ интервалов

u(1) = min(x);

u(k+1) = max(x);

du = (u(k+1) - u(1)) / k;

for i = 2: k,

u(i) = u(i-1) + du;

end;

// Вычисление частот интервалов

for i = 1: n,

for j = 1: k-1,

if u(j)<= x (i) & x (i)<u(j+1),

nu(j) = nu(j)+1;

break;

end;

if u(k)<= x (i) & x (i)<=u(k+1),

nu(k) = nu(k)+1;

end;

h = zeros(1,k+2); // Высоты

p = zeros(1,k); // Относительные частоты интервалов

uu = zeros(1,k+2); // Центры интервалов

// Вычисление высот, отн. частот инте-лов и центров инт-лов

h(1) = 0;

h(k+2) = 0;

uu(1) = u(1) - du/2;

uu(k+2) = u(k+1) + du/2;

for i = 1: k,

p(i) = nu(i) / n;

uu(i+1) = (u(i) + u(i+1)) / 2;

h(i+1) = p(i) / du;

end;

disp(u,'Границы интервалов');

disp(nu,'Частоты интервалов');

disp(p,'Относительные частоты интервалов');

disp(sum(nu),'Сумма частот');

disp(sum(p),'Сумма относительных частот');

disp(h(2:k+1),'Высоты столбцов гистограммы');

disp(ff (uu(2:k+1)),..

'Теоретическая плотность в серединах интервалов');

// построение графиков

histplot (k, x, style=2, rect=[u(1)-du, 0, u(k+1)+du, max(h)+0.02]);

// гистограмма

x = [u(1)-du: 0.0001: u(k+1)+du]; // Значение Х

//для теоретической плотности вероятностей (голубой)

disp(k);

plot2d(uu, h, 1); // Полигон частот (черный)

plot2d(x, ff (x),5);

// Теоретическая плотность вероятностей (красный)

endfunction

function [ M, D ]= dispersion21 (x)

a=2;

b=-4;

alpha=0.05;

n=400;

gamma=0.95;

k=0;

for i=1:n

k=k+ x (i);

end

c=0;

for j=1:n

c=c+(x (i))^2;

end

M =k/n;

D =(c/n)- M ^2;

endfunction

function []= dispersion22 (x)

a=2;

alpha=0.05;

n=400;

gamma=0.95;

[M,D]= dispersion21 (x);

b=(M*a+M)/(a-M*a-M)

db=abs(-4-b);

disp(db, '|b-b|');

endfunction

function []= dispersion23 (x)

//доверительные границы

a=2;

alpha=0.05;

n=400;

gamma=0.95;

[M,D]= dispersion21 (x);

interv1=(n*D)/(((2.807+sqrt(2*n-1))^2)/2)

interv2=(n*D)/(((-2.807+sqrt(2*n-1))^2)/2)

interv3=M-(1.960*(sqrt(D)/sqrt(n-1)))

interv4=M+(1.960*(sqrt(D)/sqrt(n-1)))

printf ('доверительный интервал для дисперсии (');

printf ('%f',interv1);

printf (' ');

printf ('%f',interv2);

printf (')\n');

printf ('доверительный интервал для мат.ожидания (');

printf ('%f',interv3);

printf (' ');

printf ('%f',interv4);

printf (')');

disp(M,'Мат.ожидание');

disp(D,'дисперсия');

endfunction

function []= stat2 (x)

a=2;

alpha=0.05;

n=400;

gamma=0.95;

k = floor(1 + 3.32* log10 (n)) + 1;

u = zeros(1,k+1); // Границы интервалов

nu = zeros(1,k); // Частоты интервалов

// Вычисление границ интервалов

u(1) = min(x);

u(k+1) = max(x);

du = (u(k+1) - u(1)) / k;

for i = 2: k,

u(i) = u(i-1) + du;

end;

// Вычисление частот интервалов

for i = 1: n,

for j = 1: k-1,

if u(j)<= x (i) & x (i)<u(j+1),

nu(j) = nu(j)+1;

break;

end;

if u(k)<= x (i) & x (i)<=u(k+1),

nu(k) = nu(k)+1;

end;

_u = zeros(1,k+1); // границы интервалов

_nu = zeros(1,k); // частоты интервалов

// вычисление новых интервалов и частот

_u(1) = u(1);

i = 0; // cчетчик старых значений

j = 0; // счетчик новых значений

while i<k,

j = j + 1;

while (_nu(j)<5 & i<k),

i = i + 1;

_nu(j) = _nu(j) + nu(i);

end;

_u(j+1)=u(i+1);

if (i==k & _nu(j)<5),

_nu(j-1)=_nu(j-1)+_nu(j);

_u(j) = _u(j+1);

_nu(j) = 0;

_u(j+1) = 0;

j = j - 1;

end;

function [ y ]= F (x) // функция распределения

// параметры a=teta1, b=teta2

a=-3;

b=1;

alpha=0.05;

n=450;

gamma=0.95;

if ((x >=0)&(x <1)), y = (b/(b-a))* x ^a;

else, if x >=1, y = 1+(a/(b-a))* x ^b;

else, y =0;

end;

endfunction

old_p = zeros(1,k); // старая теор. вероятность

for i = 1: k,

old_p(i) = F (u(i+1)) - F (u(i));

end;

disp(u,'границы старых интервалов');

disp(old_p,'теор. вероятности старых интервалов');

N = j; disp(N, 'новое число интервалов');

_u = _u(1:N+1); disp(_u, 'новые границы интервалов');

_nu = _nu(1:N); disp(_nu, 'новые частоты интервалов');

_p = _nu / n; disp(_p, 'новые отн. частоты интервалов');

// теоретическая вероятность

p = zeros(1,N);

for i = 1: N,

p(i) = F (_u(i+1)) - F (_u(i));

end;

disp(p, 'теоретические вероятности новых интервалов');

disp(sum(_nu),'сумма новых частот');

disp(sum(_p),'сумма новых отн. частот');

function [ ans ]= stat (N, u, p) // статистика критерия hi^2

ans = 0;

for i = 1: N,

ans = ans + (_nu(i)-n* p (i))^2 / (n* p (i));

end

endfunction

hi_2_alpha_0_98 =.. // распределение hi^2..

.. // alpha = 0.98; n <= 10..

[ 5.412, 7.824, 9.837, 11.668, 13.388,..

15.033, 16.622, 18.168, 19.679, 21.161]';

r = 2; // число неизвестных параметров

h = hi_2_alpha_0_98(N - 1 - r); // порог

t = stat (N,_u,p);

disp('параметры неизвестны');

if t >= h,

disp([t,h],..

'гипотеза отвержена (t >= h)');

else

disp([t,h],..

'гипотеза принята (t < h)');

end;

ПРИЛОЖЕНИЕ В. Задание №3

function []= model3 ();

n = 475; disp(n, 'объем выборки');

ax = 0.25; disp(ax, 'мат. ожидание X');

dx = 10.7; disp(dx, 'дисперсия X');

ay = -3.7; disp(ay, 'мат. ожидание Y');

dy = 5.0; disp(dy, 'дисперсия Y');

rxy = 0.46; disp(rxy, 'коэффициент корреляции');

alpha = 0.001; disp(alpha, 'уровень значимости');

gamma=0.999;

function [ y ]= f (x, a, d) // нормальный закон распределения N(a,d)

y = (1/sqrt(2*%pi* d)) * exp(-(x - a)^2 / (2* d));

endfunction

// выборки случайных величин X~N(ax,dx) и Y~N(ay,dy)

Z1 = grand(1,n,'nor',0,1);

Z2 = grand(1,n,'nor',0,1);

B = [sqrt(dx), 0;..

rxy*sqrt(dy), sqrt(dy*(1-rxy))..

]; // матрица преобразования

X = B(1,1)*Z1 + ax;

Y = B(2,1)*Z1 + B(2,2)*Z2 + ay;

//------------------------------------------------------

disp('');

disp('Задание 3.1');

xsr = mean (X);

disp(xsr, 'выборочное среднее случайной величины X');

disp(abs(ax-xsr),'|MX - x(среднее)|');

ysr = mean (Y);

disp(ysr, 'выборочное среднее случайной величины Y');

disp(abs(ay-ysr),'|MY - y(среднее)|');

sx2 = mean (X^2) - xsr^2;

disp(sx2, 'выборочная дисперсия случайной величины X');

disp(abs(dx-sx2),'|DX - sx^2|');

sy2 = mean (Y^2) - ysr^2;

disp(sy2, 'выборочная дисперсия случайной величины Y');

disp(abs(dy-sy2),'|DY - sy^2|');

xysr=0; for i=1:n, xysr=xysr+X(i)*Y(i); end;

r_xy = (xysr/n - xsr*ysr) / sqrt(sx2*sy2);

disp(r_xy, 'выборочный коэффициент корреляции');

disp(abs(rxy-r_xy),'|rxy - r^xy|');

//------------------------------------------------------

disp('');

disp('Задание 3.2');

k = floor(1 + 3.32* log10 (n)) + 1;

disp(k, 'число интервалов');

ux = zeros(1,k+1); // границы интервалов X

uy = zeros(1,k+1); // границы интервалов Y

nux = zeros(1,k); // частоты интервалов X

nuy = zeros(1,k); // частоты интервалов Y

nuxy = zeros(k,k); // частоты прямоугольников

// вычисление границ интервалов

ux(1) = min(X);

ux(k+1) = max(X);

uy(1) = min(Y);

uy(k+1) = max(Y);

dux = (ux(k+1) - ux(1)) / k;

duy = (uy(k+1) - uy(1)) / k;

for i = 2: k,

ux(i) = ux(i-1) + dux;

uy(i) = uy(i-1) + duy;

end;

K = k; // число интервалов X

L = k; // число интервалов Y

function [ nux, nuy, nuxy ]= countFrequencies (ux, uy)

// вычисление частот

K = size(ux,2) - 1;

L = size(uy,2) - 1;

nux = zeros(1,K); // частоты интервалов X

nuy = zeros(1,L); // частоты интервалов Y

nuxy = zeros(K,L); // частоты прямоугольников

for i = 1: n,

jx=0; jy=0;

for j = K: -1: 1, // для Х

if ux (j)<=X(i) & X(i)<= ux (j+1),

nux (j) = nux (j)+1;

jx = j;

break;

end;

for j = L: -1: 1, // для Y

if uy (j)<=Y(i) & Y(i)<= uy (j+1),

nuy (j) = nuy (j)+1;

jy = j;

break;

end;

nuxy (jx,jy) = nuxy (jx,jy) + 1;

end;

endfunction

[nux,nuy,nuxy] = countFrequencies (ux,uy);

disp(ux, 'границы интервалов X');

disp(nux, 'частоты интервалов X');

disp(nux/n, 'отн. частоты интервалов X');

disp(uy, 'границы интервалов Y');

disp(nuy, 'частоты интервалов Y');

disp(nuy/n, 'отн. частоты интервалов Y');

disp(nuxy, 'частоты прямоугольников');

disp(nuxy/n, 'отн. частоты прямоугольников');

function [ ans, ii, jj ]= minInRect (nuxy)

// находит числа меньше 5 в матрице частот

ans = 5; // минимальное число

ii =1; jj =1; // строка и столбец

[K,L] = size(nuxy);

for i = 1: K,

for j = 1: L,

if nuxy (i,j)< ans,

ans = nuxy (i,j);

ii = i;

jj = j;

return;

end;

endfunction

[min_in_rect,ii,jj] = minInRect (nuxy);

while min_in_rect < 5,

// работает, пока не выполнено условие min >= 5

if ii==K, ii=K-1; end;

if jj==L, jj=L-1; end;

if K > L,

for i = ii+1: K,

ux(i) = ux(i+1);

end;

ux = ux(1:K);

K = K - 1;

else,

for j = jj+1: L,

uy(j) = uy(j+1);

end;

uy = uy(1:L);

L = L - 1;

end;

[nux,nuy,nuxy]= countFrequencies (ux,uy);

[min_in_rect,ii,jj] = minInRect (nuxy);

end;

disp(K, 'новое число интервалов X');

disp(ux, 'новые границы интервалов X');

disp(nux, 'новые частоты интервалов X');

disp(nux/n, 'новые отн. частоты интервалов X');

disp(L, 'новое число интервалов Y');

disp(uy, 'новые границы интервалов Y');

disp(nuy, 'новые частоты интервалов Y');

disp(nuy/n, 'новые отн. частоты интервалов Y');

disp(nuxy, 'новые частоты прямоугольников');

disp(nuxy/n, 'отн. частоты новых прямоугольников');

px = zeros(1,K); // относительные частоты X

py = zeros(1,L); // относительные частоты Y

pxy = zeros(K,L); // отн. частоты прямоугольников

for i = 1: K, px(i) = nux(i) / n; end;

for i = 1: L, py(i) = nuy(i) / n; end;

for i = 1: K, for j = 1: L,

pxy(i,j) = nux(i)*nuy(j) / n^2;

end; end;

// используется критерий проверки значимости rxy

h = 2.576; // порог = (1-alpha)/2 - квантиль

// распределения Стьюдента S(n-2)

t = (r_xy*sqrt(n-2)) / sqrt(1-r_xy^2); // статистика

// используется критерий независимости hi^2

hh = cdfnor("X", (K-1)*(L-1), 2*(K-1)*(L-1),..

1-alpha, alpha); // порог

//hh = cdfnor("X", (K-1)*(L-1), 2*(K-1)*(L-1),..

// 1-alpha, alpha); // порог

st = 0;

for i = 1: K,

for j = 1: L,

st = st + (nuxy(i,j)^2) / (nux(i)*nuy(j));

end;

st = n*(st - 1); // статистика

disp('используется критерий проверки значимости rxy');

if abs(t) >= h,

disp([abs(t),h],..

'гипотеза о независимости отвержена (|t| >= h)');

else

disp([abs(t),h],..

'гипотеза о независимости принята (|t| < h)');

end;

disp('используется критерий независимости hi^2');

if abs(st) >= hh,

disp([abs(st),hh],..

'гипотеза о независимости отвержена (|t| >= h)');

else

disp([abs(st),hh],..

'гипотеза о независимости принята (|t| < h)');

end;

//------------------------------------------------------

disp('');

disp('Задание 3.3');

function [ y ]= regrYtoX (x) // регрессия Y на X

y = ysr + r_xy*sqrt(sy2/sx2)*(x -xsr);

endfunction

function [ x ]= regrXtoY (y) // регрессия X на Y

x = xsr + r_xy*sqrt(sx2/sy2)*(y -ysr);

endfunction

x = [min(X)-1: 0.001: max(X)+1]; // значения X

y = [min(Y)-1: 0.001: max(Y)+1]; // значения Y

plot2d(X,Y,0); // значения выборки

plot2d(x, regrYtoX (x),5); // ур-е регрессии Y на X

plot2d(regrXtoY (y),y,5); // ур-е регрессии X на Y

disp('графики построены!');

endfunction