Оглавление
ВВЕДЕНИЕ.. 3
1. ЗАДАНИЕ И ИСХОДНЫЕ ДАННЫЕ.. 4
1.1. Содержание задания. 4
1.2. Исходные данные. 5
2. ВЫПОЛНЕНИЕ ЗАДАНИЙ.. 6
2.1. Задание №1. 6
2.1.1. Гистограмма распределения. 6
2.1.2. Выборочные числовые характеристики. 8
2.1.3. Метод максимального правдоподобия. 8
2.1.5. Критерий Пирсона. 11
2.2. Задание №2. 13
2.2.1. Гистограмма выборки. 15
2.2.2. Выборочные числовые характеристики. 16
2.2.3. Метод моментов. 17
2.2.4. Доверительные интервалы.. 17
2.2.5. Критерий Пирсона. 18
2.3. Задание №3. 19
2.3.1. Выборочные числовые характеристики. 19
2.3.2. Гипотеза о независимости. 20
2.3.3. Уравнения регрессии. 21
Список литературы... 22
ПРИЛОЖЕНИЕ А. Задание №1. 23
ПРИЛОЖЕНИЕ Б. Задание №2. 27
ПРИЛОЖЕНИЕ В. Задание №3. 31
ВВЕДЕНИЕ
Математическая статистика — наука о математических методах анализа данных, полученных при проведении массовых наблюдений (измерений, опытов).
Один из основателей математики случайностей Блез Паскаль определили ее как «учение, объединяющее точность математических доказательств с неопределенностью случая и примиряющее эти, казалось бы, противоречивые элементы».
Математическая статистика изучает методы (в рамках точных математических моделей), которые позволяют отвечать на вопрос, соответствует ли практика, представленная в виде результатов эксперимента, данному гипотетическому представлению о природе явления или нет. При этом имеются в виду не эксперименты, которые позволяют делать однозначные, детерминированные выводы о рассматриваемых явлениях, а эксперименты, результатами которых являются случайные события. С развитием науки задач такого рода становится все больше и больше, поскольку с увеличением точности экспериментов становится все труднее избежать «случайного фактора», связанного с различными помехами и ограниченностью наших измерительных и вычислительных возможностей. Вот почему за последнее время статистические методы, проникнув в самые разнообразные области науки и техники, стали широко использоваться при анализе и обработке опытных данных.
В зависимости от математической природы конкретных результатов наблюдений математическая статистика делится на статистику чисел, многомерный статистический анализ, анализ функций (процессов) и временных рядов, статистику объектов нечисловой природы. Существенная часть математической статистики основана на вероятностных моделях. Выделяют общие задачи описания данных, оценивания и проверки гипотез. Рассматривают и более частные задачи, связанные с проведением выборочных обследований, восстановлением зависимостей, построением и использованием классификаций (типологий) и др.
ЗАДАНИЕ И ИСХОДНЫЕ ДАННЫЕ
Содержание задания
1. Смоделировать случайную величину 
, имеющую нормальный закон распределения с параметрами 
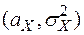. На основе выборки объема 
исследовать статистические характеристики случайной величины , решив следующие задачи.
1.1. Построить гистограмму распределения и изобразить ее графически одновременно с теоретической плотностью вероятностей.
1.2. Вычислить выборочное среднее и выборочную дисперсию.
1.3. Найти оценки математического ожидания и дисперсии методом максимального правдоподобия. Указать несмещенную оценку дисперсии.
1.4. Построить доверительные интервалы для математического ожидания и дисперсии, соответствующие доверительной вероятности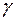 
.
1.5. Проверить гипотезу о нормальном распределении случайной величины , используя критерий 
Пирсона при уровне значимости 
.
2. Смоделировать случайную величину X, имеющую заданный непрерывный закон распределения (отличный от нормального) с заданными параметрами. На основе выборки объема исследовать статистические характеристики случайной величины X, решив следующие задачи.
2.1. Построить гистограмму распределения и изобразить ее графически одновременно с теоретической плотностью вероятностей.
2.2. Определить точечные оценки математического ожидания и дисперсии.
2.3. При заданном виде распределения построить оценки входящих в него неизвестных параметров методом моментов.
2.4. Построить доверительные интервалы для математического ожидания и дисперсии, соответствующие доверительной вероятности .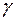
2.5. Проверить гипотезу о виде распределении случайной величины X, используя критерий Пирсона при уровне значимости .
3. Смоделировать случайный вектор 
, имеющий двумерный нормальный закон распределения с параметрами 
. На основе выборки объема исследовать статистические характеристики случайного вектора , решив следующие задачи.
3.1. Найти точечные оценки параметров, входящих в распределение.
3.2. Проверить гипотезу о независимости случайных величин и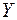 
при уровне значимости .
3.3. Найти эмпирические уравнения регрессии 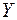на и на 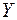и изобразить их графически одновременно с выборочными значениями.
Исходные данные
Группа 628
Вариант 21
Задача №1
| n | a | s2 | g | a |
| 0.25 | 10.7 | 0.999 | 0.001 |
Задача №2
|
Исходные данные: a = 2, b = -4, a = 0.05, g = 0.95, n = 400.
Рассчитать аналитически: MX, DX, F (x),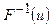 
.
Найти точечные оценки параметров a и b методом моментов.
Задача №3
Значения параметров 
заимствовать из задачи 1.
| 
| 
|
| -3.7 | 5.0 | 0.46 |
ВЫПОЛНЕНИЕ ЗАДАНИЙ
Задание №1.
Гистограмма распределения
Наблюдаем случайную величину X, которая имеет нормальный закон распределения с заданными параметрами a и 2, т.е. 
. Это значит, что плотность вероятностей случайной величины X определяется по формуле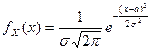 
.
Смоделируем эту случайную величину на компьютере. В процессе работы будем использовать свободный универсальный математический пакет SciLab v.5.3.3.
В этом пакете имеется функция rand, моделирующая равномерное распределение 
. С ее помощью можно смоделировать нормальное распределение, воспользовавшись формулами
,
,
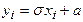где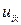 
- числа, получаемые вызовом функции rand;
- выборка, соответствующая распределению, близкому к 
,
- выборка, соответствующая распределению, близкому к 
.
Теперь по полученной выборке требуется построить гистограмму распределения.
Сначала найдём выборочные максимум и минимум:
Простым вызовом соответствующих функций в Scilab получаем:
xmin= -9.599971
xmax= 7.8887969
Количество интервалов группировки определяется по правилу Стургерса: 
. (Для вычисления десятичного логарифма используем функцию log10, для взятия целой части от числа - floor)
Ширину интервалов группировки легко определить: 
.
Таким образом, получаем k = 10, ∆=1.7488768.
Полученные данные занесём в следующую таблицу:
| Номер интервала | Интервал | 
| 
| 
| 
|
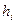
| [-9.599971; -7.8510942) | 0.0063158 | 0.0036113 | 0.0028270 | ||
| [-7.8510942; -6.1022174) | 0.0231579 | 0.0132416 | 0.0106259 | ||
| [-6.1022174; -4.3533406) | 0.0589474 | 0.0337058 | 0.0300104 | ||
| [-4.3533406; - 2.6044638) | 0.1305263 | 0.0746344 | 0.0636846 | ||
| [- 2.6044638;- 0.8555870) | 0.1642105 | 0.0938949 | 0.1015442 | ||
| [- 0.8555870; 0.8932898) | 0.2021053 | 0.1155629 | 0.1216561 | ||
| [0.8932898; 2.6421666) | 0.1852632 | 0.1059327 | 0.1095143 | ||
| [2.6421666; 4.3910434) | 0.1347368 | 0.0770419 | 0.0740739 | ||
| [4.3910434; 6.1399202 ] | 0.0568421 | 0.0325021 | 0.0376459 | ||
| [6.1399202; 7.8887969 ] | 0.0378947 | 0.0216680 | 0.0143757 | ||
| Σ |
Здесь 
– границы интервалов группировки;
– частоты значений;
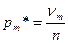– относительные частоты;
– высоты гистограммы;
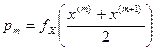– теоретические значения плотности вероятностей в серединах интервалов. Отметим, что 
.
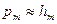Теперь одновременно изображаем гистограмму распределения и теоретическую плотность вероятности.
Для этого воспользуемся функциями plot2d и hisplot.
Выборочные числовые характеристики
У нас имеется выборка объёма n , полученная при n наблюдениях за случайной величиной X. Требуется определить выборочные числовые характеристики по этой выборке.
Аналогом математического ожидания является выборочное среднее. Оно определяется как среднее арифметическое элементов выборки: 
. В Scilab для этого предусмотрена функция mean.
Аналогом дисперсии является выборочная дисперсия. Она определяется следующим образом: 
. Здесь 
.
Для нашего случая получаем:
x=0.1515287
s2=10.70955
Отклонения от реальных значений составляют:
| a-x | = 0.0984713
| 
2-s2|=0.0095504
