Выборочные числовые характеристики. Имея выборку объёма n, полученную при n наблюдениях за случайной величиной X, требуется определить выборочные числовые характеристики по этой выборке.

Имея выборку объёма n , полученную при n наблюдениях за случайной величиной X, требуется определить выборочные числовые характеристики по этой выборке.

Аналогом математического ожидания является выборочное среднее. Оно определяется как среднее арифметическое элементов выборки: .

Аналогом дисперсии является выборочная дисперсия. Она определяется следующим образом: . Здесь .

Для нашего случая получаем:

//////x= 0.8748906 s2=0.1938406

Отклонения от реальных значений составляют:

1ое:4/9-x 2ое:11/81 – s2

 

 

Метод моментов

У нас имеется выборка объёма n , полученная при n наблюдениях за случайной величиной X, имеющей плотность вероятностей

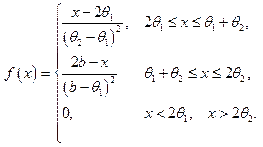
с неизвестными параметрами и . Требуется оценить значение параметров методом моментов, т.е. указать для него точечные оценки и .

Составим систему уравнений, используя найденные ранее выражения для дисперсии и математического ожидания.

 

После подсчёта получаем

Отклонение от реальных значений составляют:

|b-sigma1|=0.411393

Доверительные интервалы

Имея выборку объёма n , полученную при n наблюдениях за случайной величиной X с общим законом распределения Симпсона, требуется построить доверительные интервалы для математического ожидания и дисперсии, соответствующие доверительной вероятности γ.

В нашем случае асимптотическими доверительными интервалами для математического ожидания MX = a и DX = σ² являются:
и
,
где – выборочное среднее,
S² – выборочная дисперсия,
– выборочный центральный момент четвёртого порядка.

В результате вычислений получаем:

; \\\(0.827625 0.922156)
.\\\\(0.192243 0.286372)

Очевидно, что и найденные ранее выборочные, и теоретические значения матожидания и дисперсии попадают в полученные интервалы.

Критерий Пирсона

Пусть у нас имеется выборка объёма n , полученная при n наблюдениях за случайной величиной X, закон распределения которой неизвестен. Требуется проверить гипотезу о том, что величина X имеет общий закон распределения Симпсона с неизвестными параметрами, пользуясь критерием χ² Пирсона.

Поскольку у всех интервалов частота значений превышает 5, то нет необходимости их объединять.

Составим таблицу для интервалов группировки:

Номер интервала	Интервал
	[-0.9579396; -0.5791479)		0.025	0.0207149
	[-0.5791479; -0.2003562)		0.05	0.0584023
	[-0.2003562; 0.1784354)		0.08	0.0960898
	[0.1784354; 0.5572271)		0.16	0.1337772
	[0.5572271; 0.9360188)		0.175	0.1714647
	[0.9360188; 1.3148105)		0.175	0.1787250
	[1.3148105; 1.6936021)		0.1375	0.1414256
	[1.6936021; 2.0723938)		0.0925	0.1037381
	[2.0723938; 2.4511855)		0.075	0.0660507
	[2.4511855; 2.8299772]		0.03	0.0283632
Σ

 

Здесь – границы интервалов группировки;

– частоты значений;

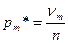– относительные частоты;

– теоретические значения вероятности попадания в интервал.

Найдём значение статистики:

, где N – количество интервалов группировки.

Получаем: . \\\\\ 8.567

Определим порог .

Здесь k=2 – число неизвестных параметров распределения.

Таким образом, искомый порог . 13.388

Сравним значение статистики и порога. Очевидно, что значение статистики меньше, чем значение порога, следовательно, можно принять гипотезу о виде распределения.

Задание №3.