Парна регресія.
По 12 підприємствам регіону вивчається залежність вироблення продукції на одного працівника Y (тис. грн.) від запровадження в дію нових основних фондів Х(% від вартості на кінець року).
1. Побудувати лінійне рівняння парної регресії Yx.
2. Порахувати коефіцієнт кореляції та середню похибку апроксимації.
3. Оцінити статистичну залежність параметрів регресії та кореляції за допомогою F - критерія Фішера та t - критерія Стьюдента.
4. Виконати прогноз вироблення продукції Y (тис. грн.) при прогнозному значенні Х*=1,05Хср.
5. Оцінити точність прогнозу, розрахувавши помилки прогнозу і його довірчий інтервал.
6. На одному графіку побудувати вихідні дані та теоретичну пряму. Для всіх розрахунків параметрів вибрати рівень значущості α=0,05.
| Х | 0,9 | 1,2 | 1,8 | 1,5 | 2,2 | 1,5 | 2,6 | 3,3 | 3,8 | 2,9 | ||
| Y | 1,2 | 3,1 | 5,3 | 4,7 | 6,5 | 7,4 | 6,3 | 4,8 | 9,6 | 14,5 | 18,7 | 11,8 |
Рішення:
1) По даним задачі будуємо варіаційний ряд:
| Х | 0,9 | 1,2 | 1,5 | 1,5 | 1,8 | 2,2 | 2,6 | 2,9 | 3,3 | 3,8 | ||
| Y | 1,2 | 3,1 | 4,7 | 4,8 | 5,3 | 6,3 | 6,5 | 7,4 | 9,6 | 11,8 | 14,5 | 18,7 |
Для розрахунків даних задачі побудуємо таблицю:
| N | X | Y | XY | X2 | Y2 | Yx | Y-Yx | IY-YxI | A:IY-YxI/Y | (Y-Yx)2 | Yср | Yх- Yср | (Yх- Yср)2 |
| 0.9 | 1.2 | 1,08 | 0,81 | 1,44 | 0.72 | 0.48 | 0.48 | 0.4 | 0.23 | 7.83 | -7,105 | 50.48 | |
| 1.2 | 3.1 | 3,72 | 1,44 | 9,61 | 2.43 | 0.67 | 0.67 | 0.21 | 0.44 | 7.83 | -5,395 | 29.11 | |
| 1.5 | 4.7 | 7,05 | 2,25 | 22,09 | 4.15 | 0.55 | 0.55 | 0.12 | 0.3 | 7.83 | -3.675 | 13.51 | |
| 1.5 | 4.8 | 7,2 | 2,25 | 23,04 | 4.15 | 0.65 | 0.65 | 0.14 | 0.42 | 7.83 | -3.675 | 13.51 | |
| 1.8 | 5.3 | 9,54 | 3,24 | 28,09 | 5.87 | -0.57 | 0.57 | 0.11 | 0.32 | 7.83 | -1.955 | 3.82 | |
| 6.3 | 12,6 | 39,69 | 7.01 | -0.71 | 0.71 | 0.11 | 0.51 | 7.83 | -0.815 | 0.66 | |||
| 6.5 | 42,25 | 7.01 | -0.51 | 0.51 | 0.08 | 0.26 | 7.83 | -0.815 | 0.66 | ||||
| 2.2 | 7.4 | 16,28 | 4,84 | 54,76 | 8.16 | -0.76 | 0.76 | 0.1 | 0.58 | 7.83 | 0.335 | 0.11 | |
| 2.6 | 9.6 | 24,96 | 6,76 | 92,16 | 10.45 | -0.85 | 0.85 | 0.09 | 0.72 | 7.83 | 2.625 | 6.89 | |
| 2.9 | 11.8 | 34,22 | 8,41 | 139,24 | 12.17 | -0.37 | 0.37 | 0.03 | 0.13 | 7.83 | 4.345 | 18.87 | |
| 3.3 | 14.5 | 47,85 | 10,89 | 210,25 | 14.46 | 0.04 | 0.04 | 7.83 | 6.635 | 44.02 | |||
| 3.8 | 18.7 | 71,06 | 14,44 | 349,69 | 17.32 | 1.38 | 1.38 | 0.07 | 1.91 | 7.83 | 9.495 | 90.15 | |
| Σ | 25,7 | 93,9 | 248,56 | 63,33 | 1012,31 | 1,47 | 5.84 | 271.81 | |||||
| Середнє значення | 2,14 | 7,83 | 20,71 | 5,28 | 84,36 | ||||||||
| σ | 0.83 | 4.81 | |||||||||||
| σ2 | 0.69 | 23.13 |
Розрахуємо параметри лінійного рівняння парної регресії Yx=a+bx. Для чого скористаємось формулами:
b= 
= 
, a= 
=7.83-5.73*2.14=-4.44.
Yx=a+bx=-4,44+5,73х – рівняння лінійної парної регресії.
σ(x)2= 
, σ(x)=0.83
σ(y)2= 
, σ(y)=4.81
Рівняння лінійної регресії завжди доповнюється показником тісноти зв’язку парної кореляції Пірсона:
rxy=b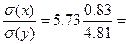 
0.989
Близкість коефіцієнта кореляції к 1 показує на тісний лінійний зв'язок між признаками х та у.
Коефіцієнт детермінації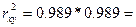 
0,978 показує, що рівняння регресії пояснює 97,8% дисперсії результативного признаку, а на долю інших факторів приходиться лише 2,2%.
Оцінемо якість рівняння регресії в цілому за допомогою F – критерія Фішера:
F= 
= Fфакт= 
або F= 
Табличне значення (k1=1, k=n-2=10, α=0.05) Fтабл=4,96.
Так, як Fфакт> Fтабл, то визнаємо статичну значимість рівняння регресії в цілому.
Для оцінки статичної значимості коефіцієнтів регресії та кореляції розрахуємо t – критерій Стьюдента і довірчі інтервали кожного з показників.
Розрахуємо випадкові похибки параметрів регресії та коефіцієнта кореляції:
В парній регресії оцінюють не тільки рівняння в цілому а і по його параметрах а та в. Для цього по кожному з параметрів визначається його стандартна похибка m(a) i m(b).
Стандартна похибка коефіцієнта регресії m(b) визначається по формулі:
m(b)= 
Стандартна похибка параметра а визначається по формулі:
m(a)= Sзал 
Стандартна похибка коефіцієнта кореляції Пірсона m(r) визначається по формулі:
m(r)=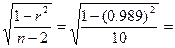 
0.046
Для оцінок сущності коефіцієнтів ta, tb, tr визначаємо іх фактичні значення і порівнюємо з табличним t(α,k) значенням при k=n-2 ступенях вільності:
tb=b/m(b)=5.73/0.266=21,5
ta=а/m(a)=-4.44/0.624=-7,11
tr=r/m(r)=0.989/0.046=21.5
t(0.05,10)=2.2281
Табличне значення t- критерія Стьюдента при α=0,05 та числі ступенів вільності k=n-2=10 дорівнює tтаб=2,2281. Так як, |tb|> tтаб, |ta|> tтаб, |tr|> tтаб, то визнаємо статичну значимість параметрів регресії а та в і показника r.
a± tтабm(a)=-4.44±2.2281*0.624=-4.44±1.39
b± tтабm(b)=5.73±2.2281*0.266=5.73±0.59
Получаємо,що а є[-5,83;-3,05], b є[5.14;6.22]
Розрахуємо середню похибку апроксимації:
А=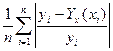 
*100%=(1,47*100%)/12=12,24% - середня похибка апроксимації.
Цє, свідчить за те, що по даних задачі підбір лінійної моделі відхиляється більш ніж на 10%.
Розрахуємо прогнозне значення Yx(xp), де xp=1.05* 
:
Xp=1.05*2.14=2.25.
Yx(xp)=Yx(2.25)=8.44
Оцінемо точність прогнозу, розрахувавши похибку прогнозу та його довірчий інтервал:
Yx(xp) ±∆p
∆p=tтаб*m(xp)=2,2281* m(xp)
m(xp)= Sзал(1+1/n + 
)1/2=0.79
∆p=2.2281*0.79=1.76
Yx(xp) ±∆p=8.44 ±1.76
Yx(xp)є[6.68,10.2]
Побудуємо на одному графіку вихідні дані та теоретичну пряму:
| |||||||||||
Додаток Е
Математико-статистичні таблиці
E.1. Таблиця значень 
-критерія Фішера при рівні значищості 
| 
| |||||||||
| 161,5 | 199,5 | 215,7 | 224,6 | 230,2 | 233,9 | 238,9 | 243,9 | 249,0 | 254,3 | |
| 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,41 | 19,45 | 19,50 | |
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,74 | 8,64 | 8,53 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,91 | 5,77 | 5,63 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,53 | 4,36 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,00 | 3,84 | 3,67 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,57 | 3,41 | 3,23 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,12 | 2,93 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,07 | 2,90 | 2,71 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,91 | 2,74 | 2,54 | |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 2,95 | 2,79 | 2,61 | 2,40 | |
| 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,85 | 2,69 | 2,50 | 2,30 | |
| 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,77 | 2,60 | 2,42 | 2,21 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,70 | 2,53 | 2,35 | 2,13 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,64 | 2,48 | 2,29 | 2,07 | |
| 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,59 | 2,42 | 2,24 | 2,01 | |
| 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,55 | 2,38 | 2,19 | 1,96 | |
| 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,51 | 2,34 | 2,15 | 1,92 | |
| 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,48 | 2,31 | 2,11 | 1,88 | |
| 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,45 | 2,28 | 2,08 | 1,84 | |
| 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,42 | 2,25 | 2,05 | 1,81 | |
| 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,40 | 2,23 | 2,03 | 1,78 | |
| 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,38 | 2,20 | 2,00 | 1,76 | |
| 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,36 | 2,18 | 1,98 | 1,73 | |
| 4,24 | 3,38 | 2,99 | 2,76 | 2,60 | 2,49 | 2,34 | 2,16 | 1,96 | 1,71 | |
| 4,22 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,32 | 2,15 | 1,95 | 1,69 | |
| 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,30 | 2,13 | 1,93 | 1,67 | |
| 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,44 | 2,29 | 2,12 | 1,91 | 1,65 | |
| 4,18 | 3,33 | 2,93 | 2,70 | 2,54 | 2,43 | 2,28 | 2,10 | 1,90 | 1,64 | |
| 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,27 | 2,09 | 1,89 | 1,62 | |
| 4,12 | 3,26 | 2,87 | 2,64 | 2,48 | 2,37 | 2,22 | 2,04 | 1,83 | 1,57 | |
| 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,18 | 2,00 | 1,79 | 1,51 | |
| 4,06 | 3,21 | 2,81 | 2,58 | 2,42 | 2,31 | 2,15 | 1,97 | 1,76 | 1,48 | |
| 4,03 | 3,18 | 2,79 | 2,56 | 2,40 | 2,29 | 2,13 | 1,95 | 1,74 | 1,44 | |
| 4,00 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,10 | 1,92 | 1,70 | 1,39 | |
| 3,98 | 3,13 | 2,74 | 2,50 | 2,35 | 2,23 | 2,07 | 1,89 | 1,67 | 1,35 | |
| 3,96 | 3,11 | 2,72 | 2,49 | 2,33 | 2,21 | 2,06 | 1,88 | 1,65 | 1,31 | |
| 3,95 | 3,10 | 2,71 | 2,47 | 2,32 | 2,20 | 2,04 | 1,86 | 1,64 | 1,28 | |
| 3,94 | 3,09 | 2,70 | 2,46 | 2,30 | 2,19 | 2,03 | 1,85 | 1,63 | 1,26 | |
| 3,92 | 3,07 | 2,68 | 2,44 | 2,29 | 2,17 | 2,01 | 1,83 | 1,60 | 1,21 | |
| 3,90 | 3,06 | 2,66 | 2,43 | 2,27 | 2,16 | 2,00 | 1,82 | 1,59 | 1,18 | |
| 3,89 | 3,04 | 2,65 | 2,42 | 2,26 | 2,14 | 1,98 | 1,80 | 1,57 | 1,14 | |
| 3,87 | 3,03 | 2,64 | 2,41 | 2,25 | 2,13 | 1,97 | 1,79 | 1,55 | 1,10 | |
| 3,86 | 3,02 | 2,63 | 2,40 | 2,24 | 2,12 | 1,96 | 1,78 | 1,54 | 1,07 | |
| 3,86 | 3,01 | 2,62 | 2,39 | 2,23 | 2,11 | 1,96 | 1,77 | 1,54 | 1,06 | |
| 3,85 | 3,00 | 2,61 | 2,38 | 2,22 | 2,10 | 1,95 | 1,76 | 1,53 | 1,03 | |
|
| 3,84 | 2,99 | 2,60 | 2,37 | 2,21 | 2,09 | 1,94 | 1,75 | 1,52 |
E.2. Критичні значення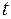 
-критерія Стьюдента при рівні значищості 0,10, 0,05, 0,01 (двохсторонній)
| Число ступеней вільності d.f. | 
| Число ступеней вільності d.f. |
| ||||
| 00,10 | 0,05 | 0,01 | 00,10 | 0,05 | 0,01 | ||
| 6,3138 | 12,706 | 63,657 | 1,7341 | 2,1009 | 2,8784 | ||
| 2,9200 | 4,3027 | 9,9248 | 1,7291 | 2,0930 | 2,8609 | ||
| 2,3534 | 3,1825 | 5,8409 | 1,7247 | 2,0860 | 2,8453 | ||
| 2,1318 | 2,7764 | 4,5041 | 1,7207 | 2,0796 | 2,8314 | ||
| 2,0150 | 2,5706 | 4,0321 | 1,7171 | 2,0739 | 2,8188 | ||
| 1,9432 | 2,4469 | 3,7074 | 1,7139 | 2,0687 | 2,8073 | ||
| 1,8946 | 2,3646 | 3,4995 | 1,7109 | 2,0639 | 2,7969 | ||
| 1,8595 | 2,3060 | 3,3554 | 1,7081 | 2,0595 | 2,7874 | ||
| 1,8331 | 2,2622 | 3,2498 | 1,7056 | 2,0555 | 2,7787 | ||
| 1,8125 | 2,2281 | 3,1693 | 1,7033 | 2,0518 | 2,7707 | ||
| 1,7959 | 2,2010 | 3,1058 | 1,7011 | 2,0484 | 2,7633 | ||
| 1,7823 | 2,1788 | 3,0545 | 1,6991 | 2,0452 | 2,7564 | ||
| 1,7709 | 2,1604 | 3,0123 | 1,6973 | 2,0423 | 2,7500 | ||
| 1,7613 | 2,1448 | 2,9768 | 1,6839 | 2,0211 | 2,7045 | ||
| 1,7530 | 2,1315 | 2,9467 | 1,6707 | 2,0003 | 2,6603 | ||
| 1,7459 | 2,1199 | 2,9208 | 1,6577 | 1,9799 | 2,6174 | ||
| 1,7396 | 2,1098 | 2,8982 |
| 1,6449 | 1,9600 | 2,5758 |
Часові ряди
Маємо умовні дані про об’єм продажу товару за останні 11 кварталів.
1. Побудувати адитивну модель тимчасового ряду (для непарних варіантів) або мультиплікативну (для парних варіантів) модель часового ряду.
2. Розрахувати автокореляцію залишків побудованої моделі часового ряду. Зробити висновки.
3. Дати прогноз на об’єм продажу на два квартали вперед.
| Квартал | |||||||||||
| Об’єм продажу |
АНАЛІЗ АДИТИВНОЇ МОДЕЛІ
В таблиці дан об’єм продажу (тис. грн..) за останні 11 кварталів. На основі цих даних дамо прогноз продажу на слідуючі два квартали.
На першому кроці треба виключити сезонну варіацію скориставшись методом ковзаної середньої. Заповнюємо таблицю:
| Номер квартала | Об’єм продажу | Ковзана середня за 4 квартали | Центрована ковзана середня | Оцінка сезонної варіації | ||
| 1 рік | ||||||
| 5,625 | -0,625 | |||||
| 6,5 | 6,75 | -0,75 | ||||
| 2 рік | 7,25 | 7,625 | 1,375 | |||
| 8,5 | 0,5 | |||||
| 9,5 | -1,25 | |||||
| 9,5 | ||||||
| 3 рік | 10,5 | 11,5 | -0,5 | |||
| 12,5 | ||||||
1 рік=4 квартали. Тому знайдемо середнє значення продажу за 4 послідовних квартали. Для цього треба скласти 4 числа із другого стовпця і поділити на 4, а результат записати в (3,3):
(4+5+5+6)/4=5 (записуємо в (3,3))
(5+5+6+9)/4=6,5 (записуємо в (4,3)) і т.д.
Полусуму двох сусідніх чисел з третього записуємо в четвертий стовпець на проти верхнього із них:
(5+6,25)/2=5,625 (записуємо в (3,4))
(6,25+7,25)/2=6,75 (записуємо в (4,4)) і т.д.
Зауваження. Якщо при заповненні 3-го стовпця ковзана середня розраховується для непарного числа сезонів, то результат записуємо напроти середнього числа і дані непотрібно центрувати (тобто, стовпці 3 та 4 співпадають). 5-й стовпець – це різниця між 2 та 4 стовпцями.
Після заповнення цієї таблиці переходимо до заповнення наступної таблиці.
| Номер кварталу | Сума середніх значень | ||||
| -0,625 | -0,75 | ||||
| 1,375 | 0,5 | -1,25 | |||
| -0,5 | |||||
| Середнє значення по кварталу | 0,4 | 0,5 | -0,9 | -,04 | -0,4 |
| Скорегована сезонна варіація | 0,5 | 0,6 | -0,8 | -0,3 | 0,0 |
Оцінки сезонної варіації записуємо під номером свого кварталу. В кожному стовпці (кварталу) рахуємо середнє = (сума чисел в стовпці / кількість чисел в стовпці). Результат записуємо в строчці «Середнє значення по кварталу» (округляємо до однієї цифри після коми). Сума середніх значень по кварталах дорівнює -0,4.
Скоригуємо середнє значення середніх так, щоб загальна сума дорівнювала 0. Це необхідно, щоб усереднити значення сезонної варіації в цілому за рік. Скорегована сезонна варіація розраховується таким чином: сума оцінок сезонних варіацій (-0,4) ділиться на 4 (число кварталів в році). Тому із кожного числа цієї строки треба відняти -0,4/4=-0,1. В останній строчці получені значення сезонної варіації для кожного кварталу року.
Проводимо десезоналізацію даних, виключивши сезонну варіацію:
| Номер квартала | Об’єм продажу A | Сезонна варіація S | Десезоналізований об’єм продажу A-S=T+E | ||
| 1 рік | 0,5 | 3,5 | |||
| 0,6 | 4,4 | ||||
| -0,8 | 5,8 | ||||
| -0,3 | 6,3 | ||||
| 2 рік | 0,5 | 8,5 | |||
| 0,6 | 8,4 | ||||
| -0,8 | 8,8 | ||||
| -0,3 | 10,3 | ||||
| 3 рік | 0,5 | 10,5 | |||
| 0,6 | 12,4 | ||||
| -0,8 | 16,8 |
Виключивши сезонну варіацію приступаємо до побудови рівняння тренду Т= а + вх (рівняння лінійної парної регресії). Знайдемо коефіцієнти рівняння тренду а та в, заповнивши розрахункову таблицю:
| № | x | y | x*x | xy | в =  =  1,1
|
| 3,5 | 3,5 | ||||
| 4,4 | |||||
| 5,8 | 17,4 | ||||
| 6,3 | 24,8 | ||||
| 8,5 | 42,5 | ||||
| 8,4 | |||||
| 8,8 | 61,6 | ||||
| 10,3 | 81,6 | а=  =  2,1
Т= а + в х = 2,1 + 1,1х
| |||
| 10,5 | 94,5 | ||||
| 12,4 | |||||
| 16,8 | 184,8 | ||||
| Σ | 95,7 | 695,1 |
Розрахуємо похибки, заповнивши таблицю:
| Номер кварталу | Об’єм продажу A | Десезонолізований об’єм продажу A-S= T+E | Трендовє значення T = a +bx | Похибка ei | |ei| | |ei|2 | ||
| 1 рік | 3,5 | 3,2 | 0,3 | 0,3 | 0,09 | |||
| 4,4 | 4,3 | 0,1 | 0,1 | 0,04 | ||||
| 5,8 | 5,4 | 0,4 | 0,4 | 0,16 | ||||
| 6,3 | 6,5 | -,02 | 0,2 | 0,09 | ||||
| 2 рік | 8,5 | 7,6 | 0,9 | 0,9 | 0,81 | |||
| 8,4 | 8,7 | -0,3 | 0,3 | 0,04 | ||||
| 8,8 | 9,8 | -1 | ||||||
| 10,3 | 10,9 | -0,6 | 0,6 | 0,49 | ||||
| 3 рік | 10,5 | -1,5 | 1,5 | 2,25 | ||||
| 12,4 | 13,1 | -0,7 | 0,7 | 0,36 | ||||
| 16,8 | 14,2 | 2,6 | 2,6 8,4 | 6,76 12,06 |
Від чисел третього стовпця віднімаємо числа четвертого стовпця і результат записуємо у п’ятий стовпець.
Середнє абсолютне відхилення MAD=Σ|ei|/n=0.76. Середня квадратична похибка MSE=Σ ei|2/n=1,1. Ми бачимо, що похибки достатньо великі, це відобразиться на прогнозі.
Дамо прогноз на наступні два квартали:
T(12)= (2.1 + 1.1*12)+ (-0.3)=15.0
T(13)= (2.1 + 1.1*13) + (0.5) = 16.9.
Перевіремо гіпотезу о наявності автокореляції в залишках. Вихідні данні та проміжні розрахунки заносимо в таблицю:
| t | T | et | et-1 | (et - et-1)2 | (et)2 | Розрахуємо фактичне значення критерія Дарбіна-Уотсона за формулою:
d=  1.34
|
| 3,2 | 0,3 | 0,09 | ||||
| 4,3 | 0,1 | 0,3 | 0,04 | 0,04 | ||
| 5,4 | 0,4 | 0,1 | 0,09 | 0,16 | ||
| 6,5 | -,02 | 0,4 | 0,36 | 0,09 | ||
| 7,6 | 0,9 | -,02 | 1,21 | 0,81 | ||
| 8,7 | -0,3 | 0,9 | 1,44 | 0,04 | ||
| 9,8 | -1 | -0,3 | 0,49 | |||
| 10,9 | -0,6 | -1 | 0,16 | 0,49 | ||
| -1,5 | -0,6 | 0,81 | 2,25 | |||
| 13,1 | -0,7 | -1,5 | 0,64 | 0,36 | ||
| 14,2 | 2,6 | -0,7 | 10,89 16,13 | 6,76 12,06 |
Алгоритм виявлення автокореляції в залишках наступний:
1. Висуваємо гіпотезу Н0 – автокореляція в залишках відсутня.
2. Альтернативні гіпотези Н1 та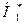 
. Н1 – автокореляція в залишках позитивна; 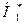- автокореляція в залишках від’ємна.
3. Далі по таблиці (додаток Е.3.) знаходимо критичні точки значення критерія Дарбіна – Уотсона для n, числа незалежних змінних моделі k і рівня значущості α. По цим значенням відрізок [0;4] розбивають на п’ять відрізків. Якщо:
1) 0<dфакт<dL – є позитивна автокореляція в залишках, Н0 відхиляється, з ймовірністю Р=1- α приймається гіпотеза Н1.
2) dL<dфакт<du – зона невизначеності;
3) du<dфакт<4 – du – приймається гіпотеза Н0, тобто автокореляція в залишках відсутня;
4) 4 – du<dфакт<4 – dL – зона невизначеності;
5) 4 – dL<dфакт<4 – є від’ємна автокореляція в залишках, Н0 відхиляється, з ймовірністю Р=1- α приймається гіпотеза .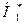
При n=11, k=1 та α=0.05 з додатку Е.3. знаходимо dL=0,93, du=1,32.
Ці дані свідчать, що ми знаходимось на відрізку 3) du<dфакт<4-du (1.32<1,34<2.68). Тобто, приймається гіпотеза Н0, що автокореляція в залишках відсутня.
