Теоретические сведения.
Тест - измерение или испытание, проведенное с целью определения состояния и способности спортсмена.
Надежность теста – степень совпадения результатов при повторном тестировании одних и тех же людей (других объектов) в одинаковых или приблизительно одинаковых условиях.
Существует несколько способов установления надежности тестов. Каждый из этих способов имеет свои особенности, свои преимущества и свои недостатки. В данной работе будет рассмотрен один из самых распространенных способов определения надежности тестов. Он основан на вычислении парного линейного коэффициента корреляции по формуле Браве-Пирсона:
 , n – число значений признаков,
, n – число значений признаков,
S-знак суммирования всех значений от 1 до n,
xi, yi - ответственно значения признаков Х и У от1 до n
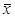 и
и 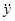 - соответственно средние арифметические значения признаков Х и У,
- соответственно средние арифметические значения признаков Х и У,
sх и sу – средние квадратичные отклонения значений признаков Х и У.
| Таблица 5-1. Значения теста и ретеста | |||||
| Номер испытания | … | n | |||
| Значения Х (тест) | |||||
| Значения У (ретест) |
Элементы формулы z (формула Браве-Пирсона) находятся в результате последовательного выполнения ниже следующих пунктов.
1 .Запись поступивших значений. Для того что бы воспользоваться формулой, делается выборка исследуемых объектов, для которых проводится тестирование Х и тестирование У, имеющих одинаковое число ответов (значений, измерений). При этом, иногда Х называется тестом, У – называется ретестом.
Полученные результаты заносятся в вспомогательную таблицу 5-1.
2. Построение макета таблицы Р езультаты вычислений, связанные с обработкой данных записываются в таблицу 5-2. В столбик 2 и 3 этой таблицы уже надо записать значения теста Х и ретеста У, которые суммируются.
3. Вычисление средних значений признаков Х и У.
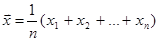

или  = S2 / n
= S2 / n 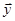 = S3 / n
= S3 / n
4. Отклонение признаков Х и У от средних значений Находится разность между каждым значением признака и соответствующим значением среднего.
(х1-  ), (х2-
), (х2-  ), (х3-
), (х3- 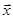 ), …, (хi –
), …, (хi –  ) – записываются в столбик 4
) – записываются в столбик 4
(у1- 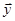 ), (у2 -
), (у2 - 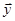 ), (у3 -
), (у3 - 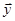 ), …, (уi -
), …, (уi - 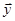 ) - записываются в столбик 5
) - записываются в столбик 5
5. Вычисляются произведения
(х1-  )· (у1-
)· (у1- 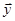 ), (х2-
), (х2-  )·(у2 -
)·(у2 - 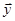 ), (х3-
), (х3- 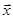 )·(у3 -
)·(у3 - 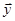 ), …, (хi –
), …, (хi –  )·(уi -
)·(уi - 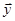 ). Результаты заносятся с столбик 6 и суммируются.
). Результаты заносятся с столбик 6 и суммируются.
6. Квадраты отклонений. Возводятся в квадрат последовательно отклонения теста и ретеста от их средних значений.
(х1-  )2, (х2-
)2, (х2-  )2, (х3-
)2, (х3- 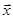 )2, …, (хi –
)2, …, (хi –  )2 – записываются в столбик 7
)2 – записываются в столбик 7
(у1- 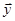 )2, (у2 -
)2, (у2 - 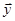 )2, (у3 -
)2, (у3 - 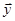 )2, …, (уi -
)2, …, (уi - 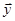 )2 - записываются в столбик 8
)2 - записываются в столбик 8
Значения в столбиках 7 и 8 суммируются.
7. Вычисление средних квадратичных отклонений Они вычисляются по формулам:
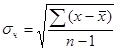 или
или 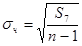 ;
; 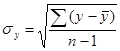 или
или 
| Таблица 3. Значения парного линейного коэффициента | |
| Значение z | Надежность |
| 0,99-0,95 | Отличная |
| 0,94-0,90 | Хорошая |
| 0,89-.0,80 | Средняя |
| 0,79-0,70 | Приемлемая |
| 0,69-0,60 | Низкая |
8. Вычисление парного линейного коэффициента корреляции. Используется формула, которую можно записать применительно к таблице 4-2 несколько иначе:
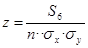
Контроль над физической подготовленностью спортсмена одна из составляющих в работе учителя, тренера, исследователя. При этом возможны варианты тестирования. Например:
| Таблица 5-2. Численные значения для расчета коэффициентов корреляции | |||||||
| № | Тест xi | Ретест уi | Отклонение | Произведение
(хi – 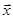 )· (уi - )· (уi - 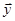 ) )
| Квадрат отклонения | ||
(хi –  ) )
| (уi - 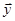 ) )
| (хi – 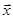 )2 )2
| (уi - 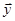 )2 )2
| ||||
| … | |||||||
| n | |||||||
| Сумма | S2= | S3= | S6= | S7= | S8= |
-Оценка одного уровня и структуры одного качества (выносливость, прыгучесть и т.д.)
-Оценка уровня одного из проявленных качеств (скорость выносливости, длительность силовой нагрузки и т.д.)
Вычисленный коэффициент z по соответствующим формулам сравнивается с показателями таблицы 3 и делается нужный вывод.






