| Таблица 4-1. Показатели теста и ретеста | ||||
| Номер испытуемого | … | n | ||
| Показатель Х | ||||
| Показатель У |
1. Заполнение таблицы. Испытания (наблюдения, тестирование) можно проводить по всей группе или сформировать некоторую выборку их n объектов. Объекты нумеруются произвольным образом, натуральными числами от 1 до n. Для каждого объекта устанавливаются числовые значения рассматриваемых признаков Х и У, которые заносятся в специальную таблицу 4-1.
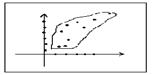
2. Построение системы координат.
а). Строится прямоугольная система координат. По оси ОХ откладываются значения показателя Х, по оси ОУ – значения показателя У. Значения берутся из таблицы 4-1.
| Таблица 4-2. Статистические результаты | |||||
| Номер испытуемого | Значение показателей | Квадрат показателей | Произведение показателей хi· yi | ||
| хi | yi | хi2 | yi2 | ||
| … | |||||
| n | |||||
| Сумма | S2= | S3= | S4= | S5= | S6= |
б). Определяются точки с координатами: А1(х1;у1), А2(х2;у2), А3(х3;у3), …, Аn(хn;уn). Получившееся множество точек на плоскости обводится замкнутым контуром. Если протяженность контура "Слева - вверх - направо", то зависимость считается положительной. Если протяженность контура "Слева - вниз - направо", то зависимость считается отрицательной. На рисунке изображена положительная направленность.
в). Делается предварительный вывод о зависимости между Х и У.
3 Вычисление коэффициента корреляции R.
Для вычисления R составляется таблица 4-2, согласно следующим рекомендациям:
-Значения показателя Х вносятся в столбец 2 и суммируются: S2 = х1+ х2+ х3+…+ хn
-Значения показателя Х возводятся в квадрат и заносятся в столбец 4, а затем суммируются: S4 = х12+ х22+ х32+…+ хn2
-Значения показателя У вносятся в столбец 3 и суммируются: S3 = у1+ у2+ у3+…+ уn
-Значения показателя У возводятся в квадрат, заносятся в столбец 5, а затем суммируются: S5 =у12+ у22+ у32+…+ уn2
-Находится произведение показателей Х и У. Результаты заносятся в столбик 6 и суммируются: S6 = х1· y1+ х2· y2+ х3· y3+…+ хn· yn
Коэффициент корреляции R вычисляется по формуле:
4. Оценивание тесноты взаимосвязи. Теснота взаимосвязи оценивается по коэффициенту корреляции R, полученному по формуле согласно таблице 4-3.
5. Направление взаимосвязи.
- Если R>0, то имеет место прямо пропорциональная зависимость в улучшении результата.
| Таблица 4- 3.Статистическая взаимосвязь | |
| Значение коэффициента | Вид взаимосвязи |
| R=1 | Функциональная зависимость вариации не наблюдается |
| 0,7<R<0,99 | Сильная статистическая взаимосвязь |
| 0,5<R<0,69 | Средняя статистическая взаимосвязь |
| 0,2<R<0,49 | Слабая статистическая взаимосвязь |
| 0,09<R<0,19 | Очень слабая статистическая взаимосвязь |
| R<0,009 | Корреляции нет |
- Если R<0, то имеет место обратно пропорциональная зависимость в ухудшении результата
б). Регрессия.
Регрессия – приблизительное описание (аппроксимирование) диаграммы рассеивания математическим уравнением. Анализируя расположение точек, построенных на координатной плоскости согласно рекомендациям, помещенным в п-2 настоящей работы, можно с достаточной долей фантазии, усмотреть в их протяженности либо прямую, либо параболу, либо еще какую-нибудь линию. Вид такой линии определяет вид зависимости: линейная зависимость, параболическая зависимость и др. В таком случае все множество точек заменяется, соответствующей линией.
В данной работе будет рассмотрена возможность замены множества точек на координатной плоскости прямой линией, предполагая линейную зависимость.
6. Построение уравнения прямой линии.
Уравнение прямой имеет вид: y = a + bx, где a и b действительные числа, вычисляемые по следующим формулам: 
значения n и Si, берется из таблицы 4-2.
, где 
и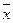 
- среднее значение показателей У и Х, которое вычисляется по, ранее приведенным формулам.
Найденные значения b и a) подставляются формулу, записанную несколько выше, т.е.
y = a + b0, что и определяет прямую линию, с помощью которой произошло аппроксимирование (сглаживание) показателей Х и У.
7. Коэффициент детерминации D. Используя коэффициент корреляции R, вычисляется коэффициент детерминации по формуле: D=R2· 100%
8. Рекомендации по анализу результатов.
Учитывая корреляцию поля, коэффициент корреляции, уравнение регрессии можно прогнозировать замену одного исследуемого действия на другое. В случае линейной регрессии можно предсказать влияние действия Х на действие У. Например, если Х: "Рост спортсмена", то можно ли предсказать У: "Высоту прыжка".
Учитывая детерминацию, уславливается процент взаимосвязи. Причем, чем больше D, тем лучше взаимосвязь.
Выполнение работы.
1. Определяются исследуемые признаки (действия) и делаются соответствующие выборки. Объем выборки не мене 25 объектов. Проводится соответствующие измерения. В случае не возможности провести эксперимент, значения признаков берутся у преподавателя. Заполняется таблица 3-1.
2. Последовательно выполняются пункты 2-8 данной работы.
3. Делаются вывод, строятся гипотезы, предположения, даются рекомендации….
***
