Метод подвійного капілярного тигля базується на підживленні робочого стопу з рідкої фази. Використання методу дозволяє або істотно поліпшити однорідність розподілу домішки вздовж зливку або вирощувати однорідно леговані кристали.
Схему установки для вирощування кристалів методом подвійного капілярного тигля наведено на рис. 4.1.
|
| 1 – кристал; 2 – робочий стоп; 3 – внутрішній (робочий) тигель; 4 – підживлюючий стоп; 5 – капілярний канал; 6 – резистивний нагрівач; 7 – загальний (підживлюючий) тигель Рисунок 4.1 - Схема установки для вирощування кристалів методом подвійного капілярного тигля |
Кристал росте з внутрішнього (робочого) тигля, розташованого усередині загального (підживлювального) тигля, сполученого з робочим тиглем капілярним каналом. У робочому режимі йде безперервний потік речовини через капіляр з підживлювального до робочого об’єму. Домішковий компонент в капілярному каналі переноситься двома потоками: потоком j ж, викликаним механічним переміщенням стопу між сполученими посудинами
j ж = f пD С,
і потоком j д, зумовленим молекулярної дифузією домішкового компонента,
j д = –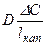 
,
де f п - швидкість подачі підживлення;
D С - різниця між концентраціями домішки в підживлювальному
і робочому об’ємах;
lкап - довжина капіляра;
D - коефіцієнт дифузії домішки в рідкій фазі.
Щоб зберегти склад підживлювального стопу незалежним від складу робочого стопу, має виконуватися умова
j ж >> j д,
тобто речовина має переноситися тільки механічним потоком стопу, а молекулярна дифузія, яка спричинює вирівнювання концентрацій домішки в робочому і підживлювальному тиглях, має бути пригнічена. Тоді для швидкості подачі підживлення f п буде справедливим вираз
f п >>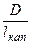 
.
Ця умова легко виконується у випадку довгих і тонких каналів.
Розподіл домішки вздовж зливку в методі подвійного
Капілярного тигля
Для розрахунку розподілу домішки вздовж зливка при використанні підживлення з рідкої фази рівняння матеріального балансу
dQ т + dQ + dQ п + dQ газ = 0, (4.1)
де dQ т, dQ, dQ п, dQ газ - зміна в процесі росту кристала кількості атомів легуючої домішки відповідно в твердій, рідкій, підживлювальній і газовій фазах. Рівняння балансу об’ємів, на відміну від (1.11), має враховувати надходження в робочий об'єм підживлювальної речовини, тому воно має бути записане в наступному вигляді:
dV т + dV + dV п= 0, (4.2)
де dV т, dV, dV п - зміна в процесі кристалізації об’єму відповідно твердої, рідкої і підживлювальної фаз.
Для характеристики об'ємних змін рідкої фази в процесі спрямованої кристалізації вводять параметр підживлення В:
В = –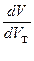 
= 1 +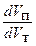 
. (4.3)
Для консервативних процесів dV = 0, тому В = 0. Для неконсервативних процесів в загальному випадку 0 < B <1.
Визначимо параметр підживлення в методі подвійного капілярного тигля. Зміна об’єму твердої фази dV т за час dt розрахуємо так:
dV т = fSdt = S спільн v оп dt,
де f - швидкість кристалізації; S - поперечний переріз кристала; S спільн - перетин спільного тигля; v оп - швидкість опускання стопу в тиглях. Зміну об'єму рідкої фази dV за час dt можна розрахувати так:
dV = – S роб v оп dt,
де S роб - поперечний переріз робочого тигля. Тоді параметр підживлення В обчислюється так:
В = – =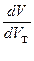 
= 
.
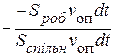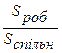Запишемо рівняння матеріального балансу (4.1) в наступному вигляді:
kСdV т + CdV + VdC + С п dV п + a F (С – С р) dt = 0. (4.4)
Оскільки частка стопу, що закристалізувався, g = 1 –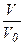 
, то dg можна виразити в наступному вигляді: dg = – 
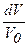. Тоді, враховуючи (4.2) і (4.3), отримуємо:
dV т = –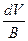 
= 
;
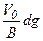dV п = – dV т – dV = (B –1) dV т = 
.
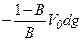Оскільки dV т = fSdt = 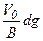, запишемо dt = 
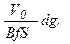Підставимо отримані співвідношення в (4.4):
kС 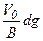– CV 0 dg + (1– g) V 0 dC – С п 
+
+ 
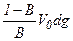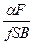V 0(C – C p) dg = 0. (4.5)
Враховуючи, що k и =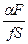 
, k об = k и + k, розділяємо в (4.5) змінні та інтегруємо, беручи до уваги, що при g = 0 концентрація домішки у стопі
С = С 0. За цих умов розподіл домішки вздовж зливку в методі подвійного капілярного тигля отримаємо в наступному вигляді:
С т =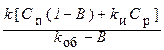 
+
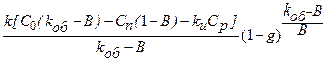. (4.6)
Розглянемо випадки, коли можливе отримання зливка з однорідним розподілом домішки при використанні методу подвійного капілярного тигля.
Перший випадок: у разі вирощування кристала в вакуумі (С р = 0) і підживлення чистою речовиною (у підживлювальному тиглі концентрація легуючої домішки С п задають рівною нулю) розподіл домішки вздовж зливку відповідно до (4.6) приводять до наступного виразу:
С т =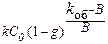 
.
Умови однорідного легування записуються так:
а) для леткої домішки (α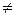 
0) і С т= kС 0, якщо k об = В. У методі подвійного капілярного тигля параметр підживлення у і має значення 0,2÷0,5. Отже, умови однорідного легування можуть бути виконані для тих домішок, у яких
k об = k + k и =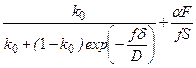 
відповідає тому ж діапазону значень.
Поверхню випаровування F в методі подвійного капілярного тигля розраховують за формулою F =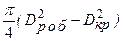 
;
б) для нелеткої домішки (α=0) умова однорідного легування має вигляд: С т= kС 0, якщо k = В. Рекомендований діапазон значень
k = 0,2÷0,5.
Другий випадок: якщо підживлювальний стоп містить легувальну домішку, тобто С п 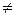0, умови однорідного легування вибирають так:
а) домішка летка (α=0). Якщо ми вибираємо співвідношення між С 0 і Сп з умови С 0(k заг – В) = С п(1 – В), то тоді відповідно до (4.6) С т =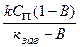 
. Дані співвідношення можуть бути реалізовані у разі, якщо k об > B, інакше домішка накопичуватиметься в рідкій фазі;
б) домішка нелетка (α = 0). Якщо ми вибираємо співвідношення між С 0 і Сп з умови С 0(k – В) = С п(1 – В), С т =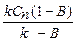 
. Дані співвідношення також можуть бути реалізовані у разі, якщо k > B.
