Цели работы
1. Научиться использовать инструмент Подбор параметра для решения нелинейных уравнений вида f (x) = 0.
2. Освоить программный инструмент Поиск решения для решения систем нелинейных уравнений в среде Excel.
3. Освоить программные средства для поиска координат и значений экстремумов функции одной переменной с помощью инструмента Поиск решения.
Задание 1
Найти все корни уравнения  .
.
Порядок выполнения работы
1. Дать рабочему листу название «Уравнение».
2. Настроить текущий документ Еxcel на вычисления с заданной точностью, открыв Настройку панели быстрого доступа и выбрав Другие команды. На вкладке Формулы задать предельное число итераций, равное 10000, и относительную погрешность, равную 0,000001.
3. Найти решение нелинейного уравнения в два этапа.
Этап – ЛОКАЛИЗАЦИЯ КОРНЕЙ
4. Создать таблицу значений функции f (x) для х Î [‑2,5; 2,5], шаг изменения 0,1.
5. Построить график функции f (x) (тип – График).
6. Основываясь на данных таблицы и графика, выделить интервалы, на которых функция меняет знак (существует корень).
Этап – УТОЧНЕНИЕ КОРНЕЙ
7. Задать начальные приближения к корням – точки из отрезков локализации корней, например: ‑2,2; 0 и 1,5. Ввести эти значения в ячейки F 16, F 17 и F 18 соответственно.
8. В ячейку G 16 ввести формулу =(F 16^3-4* F 16+1)/(ABS (F 16)+1) и с помощью маркера заполнения размножить эту формулу в ячейки G 17 и G 18.
9. На вкладке Данные выбрать Анализ «что-если»,открыть диалоговое окно Подбор параметра и заполнить его поля: в поле Установить в ячейке ввести G 16 (в этом поле дана ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения); в поле Значение ввести значение 0 (здесь указывается правая часть уравнения); в поле Изменяя значение ячейки ввести F 16 (в этом поле дана ссылка на ячейку, отведенную под переменную). После нажатия кнопки OK средство подбора параметра находит приближенное значение корня с заданной точностью.
10. Повторить указанные в п. 9 действия для ячеек G 17, F 17 и G 18, F 18 соответственно. Ячейки F 16: F 18 содержат значения корней уравнения, а ячейки G 16: G 18 – значения функции в этих точках, близкие к нулю.
11. Оформить созданный лист заголовками и комментариями, как в образце (рис. 13).
K 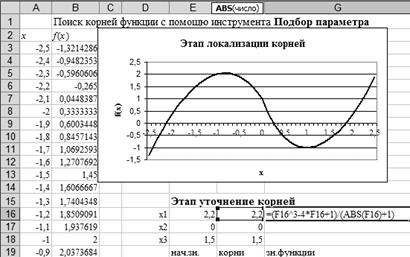
Рис. 13. Лист «Уравнение»
Задание 2
Найти решение системы нелинейных уравнений  на интервале [– 1,7; 1,7] с помощью Excel, используя инструмент Поиск решения.
на интервале [– 1,7; 1,7] с помощью Excel, используя инструмент Поиск решения.
Порядок выполнения работы
1. Дать рабочему листу название «Система».
2. Преобразовать уравнения системы относительно переменной у, получив две полуокружности в положительной и отрицательной полуплоскостях, пересекающих прямую.
3. Столбец А (аргумент x) заполнить с помощью арифметической прогрессии на интервале [– 1,7; 1,7] с шагом 0,1.
4. Столбцы B, C, D озаглавить как y 1, у 2, у 3 и заполнить формулами, соответствующими полуокружностям и прямой, используя относительную адресацию и маркер заполнения.
5. Построить графики функций системы уравнений для диапазона А 2: D 36 в одной системе координат и определить интервалы локализации корней.
6. Отредактировать диаграмму, согласно образцу (рис. 15).
7. На втором этапе – УТОЧНЕНИЕ КОРНЕЙ – найти корни системы уравнений с помощью инструмента Поиск решения.
8. Для нахождения первого корня в ячейку F 25 ввести начальное приближение для первого корня по х. В ячейку G 25 – начальное приближение для первого корня по у. В ячейку H 25 ввести формулу = (F 25^2+ G 25^2–3)^2+(2* F 25+3* G 25–1)^2
9. Чтобы получить уточненное значение первого корня, открыть диалоговое окно Поиск решения вкладки Данные. В поле Изменяя ячейки ввести диапазон ячеек F 25: G 25. В группе Равной установить переключатель в положение Значению, в поле ввода которого ввести 0. Убедитесь, что в диалоговом окне Параметры поиска решения снят флажок Линейная модель. Затем нажать кнопку Выполнить (рис. 14).
10. Вы получили приближенное решение в ячейках F 25 и G 25, а в ячейке H 25 достаточно близкое к нулю значение и с заданной точностью приблизились к точке пересечения окружности с прямой линией. Если в ячейке H 25 будет большое число, то решение найдено неверно.

Рис. 14. Инструмент «Поиск решения»
11. Аналогично находят второе решение. Но в качестве начального приближения принимают точку, близкую по координатам ко второму корню.
12. Проверить пару значений (1,5; 0). Область притяжения какого корня вы получаете?
13. Оформить созданный документ заголовками и комментариями (рис. 15).
Задание 3
Найти экстремумы функции  на интервале [‑ 2; 2] с шагом 0,1. Точность поиска e = 10-6
на интервале [‑ 2; 2] с шагом 0,1. Точность поиска e = 10-6
Порядок выполнения работы:
1. Дать рабочему листу название «Экстремум».
2. Задав значения аргумента (столбец А) и рассчитав значения функции (столбец В ), построить график функции и определить интервалы локализации экстремумов.
3. На этапе – УТОЧНЕНИЕ ЭКСТРЕМУМОВ – найти уточненные значения координат экстремумов и значения функции в этих точках с помощью инструмента Поиск решения.

Рис. 15. Лист «Система»
4. Для нахождения первого экстремума (максимума) в ячейку F 17 ввести начальное приближение, в ячейку G 17 ввести формулу = F 17^3 – F 17^2 + 4.
5. Чтобы получить уточненное значение максимума, открыть диалоговое окно Поиск решения вкладки Данные. В поле Установить целевую ячейку ввести адрес ячейки, содержащей формулу – G 17. В группе Равной установить переключатель в положение Максимальному значению. В поле Изменяя ячейки ввести адрес ячейки F 17. Затем нажать кнопку Выполнить.
6. Получено приближенное значение координаты экстремума и максимальное значение функции в ячейках F 17 и G 17.
7. Аналогично находят второй экстремум. Но при настройке диалогового окна Поиск решения в группе Равной установить переключатель в положение Минимальному значению.
8. Оформить созданный документ заголовками и комментариями (рис. 16).
Отчет о лабораторной работе должен содержать электронный документ с указанием фамилии и группы студента, времени выполнения, названия, цели лабораторной работы, выполненные задания описательной части работы и задания по предложенному преподавателем варианту.
Примечание. Если на вкладке Данные не оказалось Поиска решения, то его нужно подгрузить, используя Настройку панели быстрого доступа.
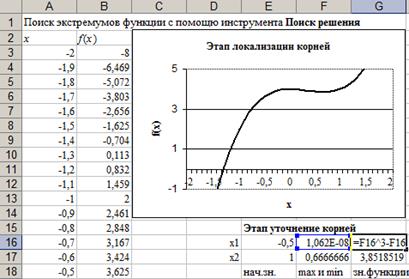
Рис. 16. Лист «Экстремум»
Задания для самостоятельного выполнения
Выполнить задания 1‑3 лабораторной работы
для заданных вариантов функций
| Вар | Решить уравнение и найти экстремум функции | Решить систему нелинейных уравнений |
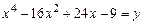
| 
| |

| 
| |
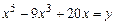
| 
| |
| 
| |

| 
|
Лабораторная работа 5






