Краткие теоретические сведения изложены в соответствующем разделе лабораторной работы 9.
Проведение анализа
Условия задачи такие же, как в соответствующем разделе лабораторной работы 9.
Ввести исходные данные, как показано на рисунке 10.1.
Рисунок 10.1 – Исходные данные
Var1 – независимая переменная – X;
Var2 – зависимая переменная – Y.
Проведем анализ в модуле Nonlinear estimation (Нелинейная оценка).
Шаг 1. Из Переключателя модулей Statistica откройте модуль Nonlinear estimation (Нелинейная оценка). Высветите название модуля и далее щелкните мышью по названию модуля Nonlinear estimation (рисунок 10.2).
Рисунок 10.2 – Запуск модуля Nonlinear estimation
Шаг 2. На экране появится стартовая панель модуля. Выберите опцию User specified regression, least squares (Метод наименьших квадратов) и далее щелкните мышью по названию модуля
(рисунок 10.3).
Рисунок 10.3 – Стартовая панель модуля Nonlinear estimation
Шаг 3. В появившемся окне щелкните мышью по кнопке Function of estimated (Предполагаемая функция) (рисунок 10.4).
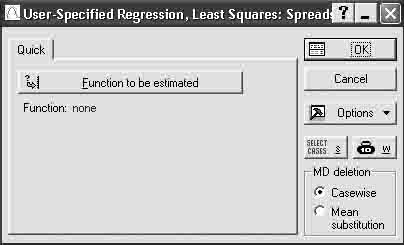
Рисунок 10.4 – Панель ввода функции
Шаг 4. В окне с клавиатуры введите предполагаемую функцию.
В отличие от подобной операции в табличном редакторе MS Excel в Statistica 6 вы можете ввести любую формулу, связывающую
зависимую и независимую переменные.
В данном случае предполагается, что наиболее подходящей функцией является полином второй степени типа:
или в конкретном случае в соответствии с таблицей исходных данных таблицы 10.1:
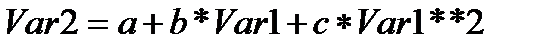(рисунок 10.5)
В нижней части рисунка приведен перечень алгебраических и функциональных символов, которые воспринимаются программой.
Нажмите OK. Затем еще раз OK.
Рисунок 10.5 – Ввод функции
Верхняя часть окна информирует о модели, методе, количестве
взятых в анализ пар. В середине окна выберите метод аппроксимации. Например: Gauss–Newton (рисунок 10.6). Нажмите OK.
Шаг 5. В верхней части появившегося окна результатов
(рисунок 10.7) показаны значения корреляционного отношения и его квадрата, 0,99 и 0,98. Это указывает на сильную корреляционную связь между переменными.
Рисунок 10.6 – Панель пуска аппроксимации
Рисунок 10.7 – Окно результатов
Шаг 6. В окне результатов щелкните мышью по кнопке Summary Parameters & standard errors (Итоговые параметры и стандартные ошибки). Полученные результаты (рисунок 10.8) подкрашены красным цветом, что свидетельствует о достоверности аппроксимации функцией:
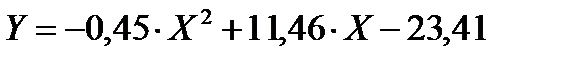
В столбце Estimate (Оценка) показаны значения коэффициентов:
a, b, c. Далее указаны стандартные ошибки, t–критерий при 22 степенях свободы, уровень значимости меньше 0,05, верхний и нижний пределы достоверности.
Рисунок 10.8 – Результаты аппроксимации
Шаг 6. Щелкните мышью по кнопке Fitted 2D function & observed vals (Подогнанная функция). На рисунке 10.9 вы увидите графическую интерпретацию корреляционной связи исходных массивов в виде заданной функции: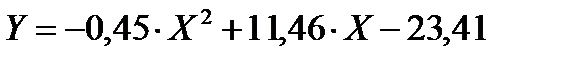
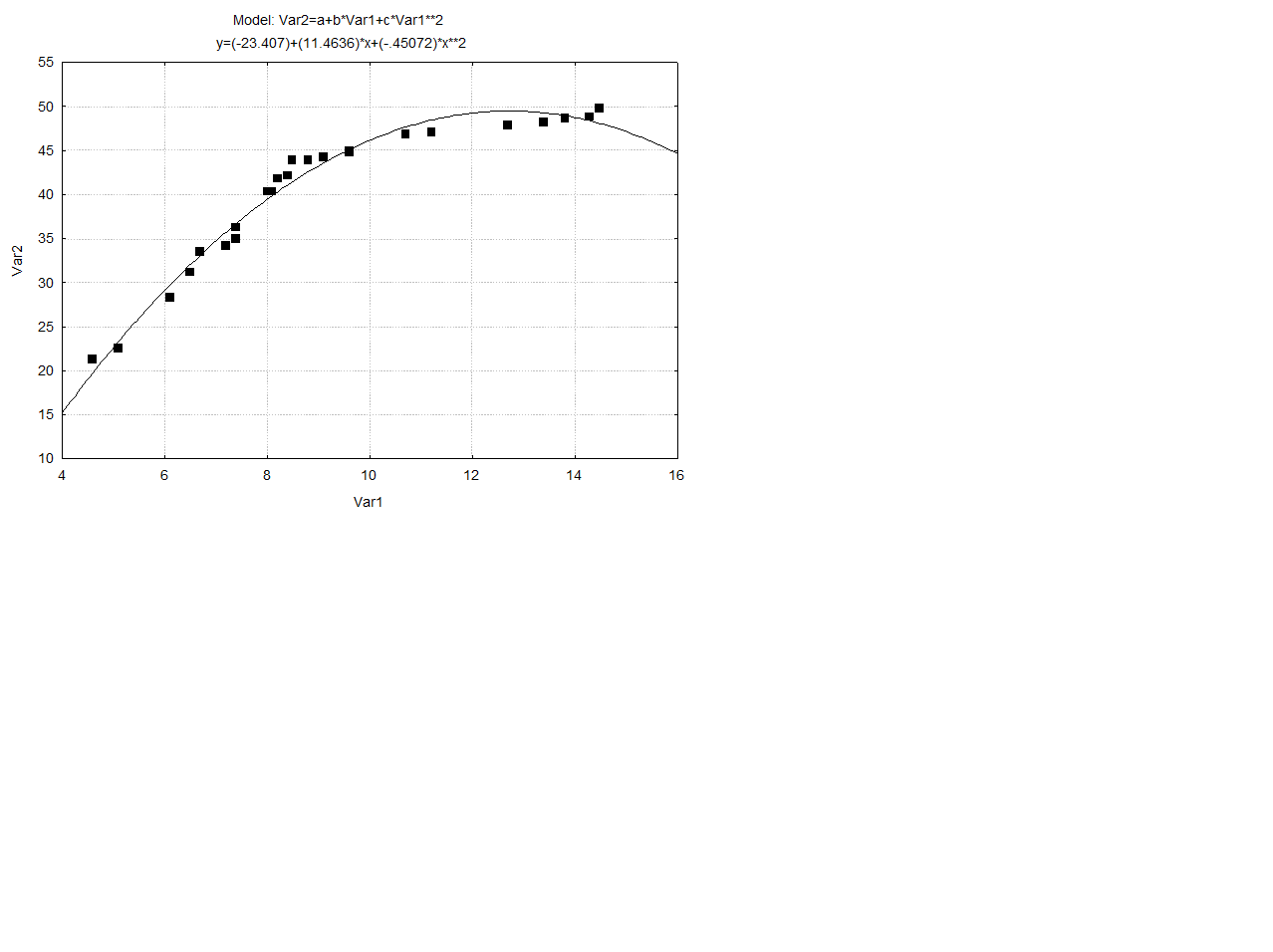
Рисунок 10.9 – Графическая интерпретация корреляционной связи
Шаг 7. В окне результатов (рисунок 10.7) в режиме Quick нажмите кнопку Analysis of Variance (Анализ вариантов). Результат
выполненной операции представлен на рисунке 10.10, который свидетельствует о достоверности регрессии (F = 8806,2 при р < 0,00..).
Рисунок 10.10 – Результат анализа вариантов
Шаг 8. В окне рисунка 10.7 перейдите в режим просмотра
результатов Residuals (Остатки). Щелкните мышью по кнопке
Observed, predicted, residual vals (Наблюдаемый, предсказанный, остаточный). Результаты выполненной операции представлены на рисунке 10.11.
Рисунок 10.11 – Наблюдаемые и аппроксимированные
значения функции
Шаг 9. Для оценки адекватности модели щелкните мышкой по
кнопке Observed vs. Predicted (Наблюдаемые против предсказанных)(рисунок 10.12).
Из рисунка видно, массивы наблюдаемых и предсказанных значений описываются линейной функцией 
. При этом k = 1 и коэффициент парной корреляции близок к 1.
Рисунок 10.12 – Визуализация результатов анализа
К заключению, сделанному в предыдущем разделе 9, следует добавить, что корреляция и регрессия достоверны, так как F = 8806,2 (рисунок 10.10) и ta = 7,8, tb = 17,9 и tc =14,1 (рисунок 10.8), что существенно выше критических значений при р < 0,00..
Задания для выполнения
1 Введите в таблицу MS Excel исходные данные из Приложения Г (таблица Г1).
2 Выполните расчетные процедуры в соответствии с порядком операций, выполненных в настоящем разделе.
Получите результат и сделайте заключение.
Лабораторная работа 11
Однофакторный дисперсионный анализ
(однофакторный комплекс в MS Excel)
Цель работы: научиться выполнять однофакторный дисперсионный анализ в программном продукте MS Excel.
