Для решения системы линейных уравнений (1) в общем случае можно также воспользоваться теоремой Кронекера-Капелли. В соответствии с теоремой система (1) совместна, если ранг расширенной матрицы 
равен рангу матрицы А.
Если система (1) совместна и ранг матрицы А равен r, то далее выполняем следующие операции:
1) выбираем в Аr линейно независимых строк и оставляем в системе (1) лишь уравнения, коэффициенты которых вошли в выбранные строки;
2) в выделенных уравнениях оставляем в левых частях такие r неизвестных, что определитель из коэффициентов при них отличен от нуля, а остальные объявляем своюодными и переносим в правые части уравнений;
3) давая свободным неизвестным произврльные числовые значения и вычисляя значения остальных неизвестных по правилу Крамера, мы получим все решения системы (1).
☺ Пример 87. Исследовать совместность и найти обшее решение и одно частное решение системы уравнений:
Решение: Выполняя стандартные операции по определению рангов матриц А и , получаем: ранги матриц равны 2 и, значит, система уравнений совместна. В качестве базового минора удобно использовать минор 2-го порядка 
, включающий первые две строки и первые два столбца матрицы. Это значит, что для дальнейшего решения системы можно использовать только первые два уравнения, а в качестве свободных неизвестных объявить, x3 и x4 .
Перепишем систему уравнений:
определитель этой системы d = -11. Далее, по правилу Крамера получаем:
, 
,
, 
.
Полученные выражения для x1 и x2 представляют общее решение заданной системы уравнений.
Одно из частных решений получим, задавая значения x3 = 0 и x4 = 1, для которых вычисляем x1 = -1 и x2 = 1.
Ответ: Общее решение: , ;
частное решение: x1 = -1, x2 = 1, x3 = 0, x4 = 1.
Пример 88. Исследовать совместность и найти обшее решение и одно частное решение системы уравнений:
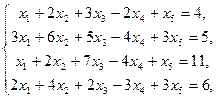
Решение: Выполняя стандартные операции по определению рангов матриц А и , получаем: ранги матриц равны 3 и, значит, система уравнений совместна. В качестве базового минора удобно использовать минор 3-го порядка 
, включающий первую, вторую и четвертую строки, а также 3,4,5-й столбца матрицы. Это значит, что для дальнейшего решения системы можно использовать только первые два и четвертое уравнения, а в качестве свободных неизвестных объявить, x1 и x2 .
Перепишем систему уравнений:
определитель этой системы d = -11. Далее, по правилу Крамера получаем:
, 
,
, 
,
, 
,
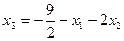Полученные выражения для x3, x4 и x5 редставляют общее решение заданной системы уравнений.
Одно из частных решений получим, задавая значения x1 = 1 и x2 = -3, для которых вычисляем 
.
Ответ: Общее решение: , , .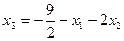
частное решение: 
.
☻ Решите примеры:
Пример 89. Исследовать совместность и найти обшее решение и одно частное решение системы уравнений:
Ответ: Общее решение: 
, 
,.
частное решение: 
.
Пример 90. Исследовать совместность и найти обшее решение и одно частное решение системы уравнений:
Ответ: Общее решение: 
, 
, 
.
частное решение: 
.
