ГЛАВА 5. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Метод последовательного исключения неизвестных
Пусть имеем систему s линейных уравнений с n неизвестными:
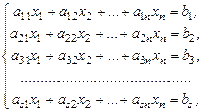(1)
где коэффициенты a ij, 
при неизвестных x i, 
и свободные члены b i, 
системы уравнений считаются заданными.
Системе уравнений (1) соответствуют: матрица системы A (составлена из коэффициентов при неизвестных) и расширенная матрица 
(составлена из всех ее коэффи-циентов, включая свободные члены):
, 
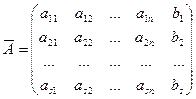(2)
Решением системы линейных уравнений (1) называется такая система n чисел (k1, k2, k3, …, kn), что каждое из уравнений (1) обращается в тождество после замены в нем неизвестных xi соответствующими числами ki,. i = 1, 2, …, n.
Метод последовательного исключения неизвестных (метод Гаусса) заключается в последовательном применении к строкам матрицы эквивалентных преобразований, приводящих исходную матрицу к «трапецоидальному» или «треугольному» (в частном случае) виду. Метод можно применять по отношению к любой системе линейных уравнений. При этом система будет несовместной, если в процессе преобразований получается уравнение, в котором коэффициенты при неизвестных равны нулю, а свободный член отличен от нуля; если же такое уравнение не встретим, то система будет совместной. Совместная система будет определенной, если она приводится к треугольному виду, и неопределенной, если приводится к трапецоидальному виду.
Рассмотрим несколько примеров, иллюстрирующих применение метода для различных возможных случаев.
☺ Пример 64. Решим систему уравнений: 
Решение: Составляем расширенную матрицу 
и применяем элементарные преобразования (эквивалентные для заданной системы):
1-й шаг: 2R-1Rх3; 3R-1R; 2-й шаг: 4R-3Rх20; 2R-3Rх21:
| -5 | -8 | 1 шаг | -5 | -8 | 2 шаг | -5 | -8 | |||||||||
| -3 | -5 | -8 | -8 | -89 | -29 | |||||||||||
| -7 | -5 | → | -8 | → | -8 | |||||||||||
| -9 | -9 | -89 | -29 |
3-й шаг: 4R-2R:
| -5 | -8 | ||||
| -89 | -29 | ||||
| -8 | |||||
| → Исходная система несовместна. |
Ответ: Система уравнений несовместная (решений нет).
Пример 65. Решим систему уравнений: 
Решение: Составляем расширенную матрицу и применяем элементарные преобразования (эквивалентные для заданной системы):
1-й шаг: 1R-5R; 2R-4R; 3R-4R; 5R-4Rх2; 2-й шаг: 3R-5R; 4R+3R; 5R-1R;:
| 1 шаг | 2 шаг | |||||||||||||||
| -2 | -5 | -2 | -5 | |||||||||||||
| -3 | -7 | -1 | ||||||||||||||
| → | → | -1 | ||||||||||||||
| -6 | -12 | -8 | -15 |
3-й шаг: 5R-2Rх4; 2R+3R; 4R+2R; 3R-2Rх3; 4-й шаг: 4R+3R; 3Rх(-1); 4-й шаг: 1R-2Rх2.
| 4 шаг | 5 шаг | |||||||||||||||
| -1 | -5 | -5 | ||||||||||||||
| → | → | |||||||||||||||
Остается считать из последнего столбца матрицы решение (3, 0, -5, 11).
Ответ: x1 = 3, x2 = 0, x3 = -5, x4 = 11.
Пример 66. Решим систему уравнений: 
Решение: Составляем расширенную матрицу и применяем элементарные преобразования (эквивалентные для заданной системы):
1-й шаг: 3R-2Rх2; 2R-1R; 4R-1Rх3; 5R-1Rх5; 2-й шаг: 1R-2R; 2R-3R; 4R-3R; 5R+2Rх3:
| 1 шаг | 2 шаг | |||||||||||||||
| -1 | -4 | |||||||||||||||
| -2 | -1 | -2 | -1 | |||||||||||||
| → | -2 | -1 | → | |||||||||||||
| -3 | -6 | -3 | -7 |
3-й шаг: 3R-2R; 5R+3R; 2R+3R; 4-й шаг: Записываем выражения для x1, x2, x3.
| |||||
| -2 | -1 |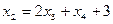 
| |||
| -6 | -3 |  , здесь x4 - свободная неизвестная
| |||
Остается выразить из последнего столбца матрицы решение, зависящее от произвольной постоянной x4.
Ответ: 
, 
, 
☻ Решите примеры:
Пример 67. Решите систему уравнений: 
Ответ: x1 = 0, x2 = 2, x3 = -2, x4 = 0, x5 = 3.
Пример 68. Решите систему уравнений: 
Ответ: Система уравнений несовместная (решений нет).
Пример 69. Решите систему уравнений: 
Ответ: 
, 
, 
.
Вопросы для самопроверки:
1. Можно ли, применяя метод Гаусса, провести полное исследование решений системы линейных уравнений с произвольным числом уравнений и неизвестных?
2. Можно ли решить систему уравнений методом Гаусса, если все значения свободных членов b i, i = 1, 2, …, n равны нулю?
3. Можно ли записать систему уравнений, представленную в Примере 69, в виде матричного уравнения AX = B?
Правило Крамера
Пусть имеем систему n линейных уравнений с n неизвестными:
(3)
где коэффициенты a ij,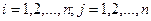 
при неизвестных x i, и свободные члены b i, системы уравнений считаются заданными.
Системе уравнений (3) соответствуют: матрица системы A (составлена из коэффициентов при неизвестных) и расширенная матрица (составлена из всех ее коэффи-циентов, включая свободные члены):
, 
(4)
Для применения правила Крамера требуется, чтобы определитель системы 
. Тогда (как показано в Гл. 3 настоящего пособия) для нахождения решения можно воспользоваться выражениями:
, 
, …, 
, (5)
где di является определителем матрицы, получающейся из матрицы А заменой i – го столбца столбцом (b 1, b 2, …, b n) матрицы .
Формулы (5) определяют единственное решение. Рассмотрим ряд примеров по применению правила Крамера.
☺ Пример 70. Решим систему уравнений: 
Решение: Последовательность вычислений при нахождении решения заданной системы:
1. Вычислим определитель системы d:
1-й шаг: 1R-2R; 4R-2R; 2-й шаг: 2R-1R; 3-й шаг: разложение по 1-му столбцу:
| -5 | 1 шаг | -5 | 2 шаг | -5 | |||||||||||||
| -3 | -6 | -3 | -6 | -7 | -13 | 3 шаг | -7 | -13 | |||||||||
| -1 | = | -1 | = | -1 | =1(-1)1+1 | -1 | |||||||||||
| -7 | -7 | -7 | -7 |
4-й шаг: 1R+3R; 3R-2Rх3; 5-й шаг: 2R-3R х2; 6 -й шаг: разложение по 1-му столбцу, вычисление определителя 2-го порядка и получение результата::
| 4 шаг | -2 | -1 | 5 шаг | -2 | -1 | ||||||
| = | -1 | = | -10 | 6 шаг | -2 | -1 | |||||
| -4 | -4 | =1(-1)3+1 | -10 | = 27 |
2. Вычислим определитель d1 для вычисления x1:
1-й шаг: 2R+3R; 1R-2R х2; 3R+2R; 2-й шаг: 2R+3R х4; 3-й шаг: разложение по 1- му столбцу; 4-й шаг: 3R-1R; 2R-3R х3;
| -5 | 1 шаг | -3 | 2 шаг | -3 | |||||||||||||
| -3 | -6 | -1 | -1 | -4 | -9 | -12 | 3 шаг | -3 | |||||||||
| -5 | -1 | = | -1 | -2 | -2 | = | -1 | -2 | -2 | =(-1)(-1)3+1 | -9 | -12 | |||||
| -7 | -7 | -7 | -7 |
4-й шаг: 3R-2R; 2R-3R х3; 5-й шаг: разложение по 3-й строке:
| 4 шаг | |||||||
| = | -3 | 5 шаг | = 81 | ||||
| -4 | -3 | =-(1) (-1)3+1 | -3 |
2. Вычислим определитель d2 для вычисления x2:
1-й шаг: 1R-2R; 2R-4R; 4R-1R; 2-й шаг: разложение по 1-му столбцу;1R+2R; 2R+1R; 3 -й шаг: выносим множитель 2 из 1-й строки; 2R+3R; 1R-3R х2;
| -5 | 1 шаг | -1 | -5 | |||||||||||||
| -6 | -12 | 2 шаг | -10 | 3 шаг | -5 | |||||||||||
| -5 | -1 | = | -5 | -1 | = (-1)1+1 | -1 | -8 | = 2∙ | -9 | |||||||
| -7 | -2 | -1 | -2 | -1 | -2 | -1 |
4-й шаг: выносим множ. 3 из 2-й строки; 1R-3R х2; 5-й шаг: разложение по 1-му столбцу; вычисление определителя 2-го порядка и получение результата:
| 4 шаг | -3 | ||||||
| = 2∙3∙ | -3 | 5 шаг | -3 | ||||
| -2 | -1 | =6∙ (-1)3+1 | -3 | = – 108 |
3. Вычислим определитель d3 для вычисления x3:
1-й шаг: 3С+4С; 4С-2С; 2-й шаг: выносим множитель 3 из 3-го столбца; 3 -й шаг: 2С-4С; 2R+1R:
| 1 шаг | 2 шаг | 3 шаг | ||||||||||||||||
| -3 | -6 | -3 | -3 | -3 | -3 | -3 | ||||||||||||
| -5 | = | -3 | = 3∙ | -1 | = 3∙ | -1 | ||||||||||||
4-й шаг: 1R-2Rх2; 4R-2R; 5-й шаг: разложение по 1-му столбцу; 3R-2R;2R-1Rх2; вычисление определителя 2-го порядка и получение результата:
| 4 шаг | ||||||||||||
| -3 | 5 шаг | |||||||||||
| = 3∙ | -1 | =3∙ (-1)2+1 | -3 | -12 | 6 шаг | -3 | -12 | |||||
| = –3∙ (-1)1+1 | = –27 |
4. Вычислим определитель d4 для вычисления x4:
1-й шаг: 1R-4Rх2; 2R-4R; 2-й шаг: разложение по 1-му столбцу; 3 -й шаг: 2С-4С; 2R+1R:
| -5 | 1 шаг | -7 | ||||||||||||||
| -3 | -7 | 2 шаг | -7 | 3 шаг | -1 | |||||||||||
| -1 | -5 | = | -1 | -5 | = (-1)4+1 | -7 | = – | -7 | ||||||||
| -7 | -7 | -1 | -5 | -1 | -5 |
4-й шаг: 2С+3Сх2; 5-й шаг: разложение по 1-й строке; вычисление определителя 2-го порядка и получение результата:
| 4 шаг | -1 | |||||||
| = – | -7 | 5 шаг | -7 | |||||
| -11 | -5 | =–(-1)∙ (-1)1+3 | -11 | = -27 | ||||
5. Вычислим неизвестные переменные:
, 
, 
,
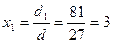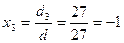Ответ: x1 = 3, x2 = -4, x3 = -1, x4 = 1.
Оценка применения правила Крамера: а) объем вычислений соответствует вычислению (n+1) -го определителей n -го порядка; б) в пределах вычисления одного определителя любая промежуточная ошибка может быть исправлена от места обнаруженной ошибки; в) представляет ценность как исследовательский инструмент: по коэффициентам исходной системы уравнений можно предсказывать получаемые результаты или вводить требования к участвующим параметрам..
☻ Решите примеры:
Пример 71. Решите систему уравнений: 
Ответ: x1 = 1, x2 = 2, x3 = -2.
Пример 72. Решите систему уравнений: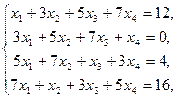 
Ответ: x1 = 1, x2 = -1, x3 = 0, x4 = 2.
Пример 73. Решите систему уравнений: 
Ответ: x1 = 0, x2 = 2, x3 = -2, x4 = -2; x5 = 1.
Вопросы для самопроверки:
1. Можно ли, применяя правило Крамера, провести полное исследование решений системы линейных уравнений с произвольным числом уравнений и неизвестных?
2. Можно ли решить систему уравнений по правилу Крамера, если все значения свободных членов b i, i = 1, 2, …, n равны нулю?
