Задача будет считаться решенной, если для ее решения установлен определенный алгоритм.
Алгоритм Евклида служит для отыскания наибольшего общего делителя двух чисел способом последовательного деления.
Пусть a и b - натуральные числа, причем a > b и a не делится на b.
Допустим, что:
1) 
,
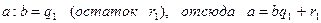2) 
,
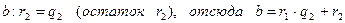3) 
,
4) 
,
…………………………………………………………………….
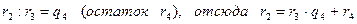n)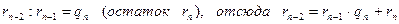 
,
n + 1)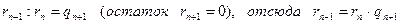 
.
Ряд равенств:
, 
, 
, 
, …, 
, 
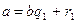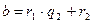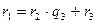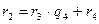, выражающих зависимость между делимым, делителем, частным и остатком при последовательном делении большего числа на меньшее, меньшего на первый остаток, первого остатка на второй остаток и т. д., известен под названием алгоритма Евклида.
Рассматриваемый ряд равенств конечен. В самом деле, по смыслу деления ряд остатков (следовательно, и ряд делителей)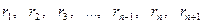 
есть ряд убывающих целых чисел, который обязательно должен закончиться некоторым остатком 
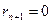, вследствие того, что число возможных остатков конечно, так как оно не может быть больше числа b. Итак, каковы бы ни были числа a и b, в результате последовательного деления большего числа на меньшее, меньшего на первый остаток, первого остатка на второй остаток и т. д., мы обязательно получим некоторый остаток 
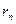, на который предыдущий остаток 
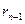разделится без остатка, и, следовательно, число 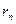будет последним, не равным нулю остатком, а значит, т последним делителем. Таким образом, возможность дальнейшего деления отпадает.
Пример. Найти НОД чисел 852 и 192.
Решение
1. Делим большее число на меньшее:
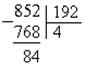
2. Делим делитель 192 на остаток 84:
3. Новый делитель делим на полученный остаток:
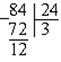
4. Снова делитель делим на остаток:
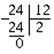
В остатке получился нуль, значит процесс деления следует прекратить. Последний делитель (12) и будет наибольшим общим делителем чисел 852 и 192.
Ответ: НОД (852, 192) = 12
Правило для нахождения НОД двух чисел способом последовательного деления.
Теорема. Чтобы найти НОД двух чисел способом последовательного деления, надо большее из данных чисел разделить на меньшее, затем, меньшее - на первый остаток, первый остаток - на второй, второй - на третий и т. д. до тех пор, пока не получится в остатке 0. Тогда последний делитель (иначе, последний не равный нулю остаток) будет наибольшим общим делителем данных чисел.
Евклид применял свой алгоритм не только в арифметике, но и в геометрии для отыскания общей меры двух отрезков путем последовательного наложения.
Основные свойства НОД
Теорема 1. На всякое число, на которое делятся без остатка два данных числа, делится и их наибольший общий делитель.
Пример. НОД (3540; 450) = 30. Кроме того, данные числа 3540 и 450 имеют общие делители 1. 2, 3, 5, 6, 10, 15.
Очевидно, что на каждый из этих общих делителей делится без остатка НОД чисел 3540 и 450, т. е. число 30.
Теорема 2. Всякое число, на которое делится без остатка наибольший общий делитель двух данных чисел, есть общий делитель этих чисел.
Пример. НОД (3540; 450) = 30. Делителями 30 являются числа: 1. 2, 3, 5, 6, 10, 15. Очевидно, что на каждое из этих чисел делятся 3540 и 450.
Теорема 3. Если каждое из двух данных чисел a и b умножить на какое-либо натуральное число m, то и наибольший общий делитель данных чисел умножится на то же число m.
Пример. НОД (558; 540) = 18. Умножив каждое из данных чисел на 2, будем иметь: НОД (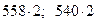
) = 36.
