Ламинарное течение — течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления).
Ламинарное течение возможно только до некоторого критического значения числа Рейнольдса, после которого оно переходит в турбулентное. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.). Например, для течения в круглой трубе 
.
Турбулентность — явление, заключающееся в том, что при увеличении интенсивности течения жидкости или газа в среде самопроизвольно образуются многочисленные нелинейные фрактальные волны и обычные, линейные различных размеров, без наличия внешних, случайных, возмущающих среду сил и/или при их присутствии. Для расчёта подобных течений были созданы различные модели турбулентности.
Сила вязкого трения
Сила вязкого трения пропорциональна скорости относительного движения V тел, пропорциональна площади S и обратно пропорциональна расстоянию между плоскостями h.
Коэффициент пропорциональности, зависящий от сорта жидкости или газа, называют коэффициентом динамической вязкости. Самое важное в характере сил вязкого трения то, что тела придут в движение при наличии сколь угодно малой силы, то есть не существует трения покоя. Это отличает вязкое трение от сухого.
Число Рейнольдса
Число Рейнольдса — безразмерное соотношение, которое, как принято считать, определяет ламинарный или турбулентный режим течения жидкости или газа. Число Рейнольдса также считается критерием подобия потоков.
Число Рейнольдса определяется следующим соотношением: 
, где ρ — плотность среды, v — характерная скорость, l — характерный размер, μ — динамическая вязкость среды.
Переход от ламинарного к турбулентному режиму происходит по достижении так называемого критического числа Рейнольдса Rekp. При Re < Rekp течение происходит в ламинарном режиме, при Re > Rekp возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.). Например, для течения в круглой трубе .
Число Рейнольдса как критерий перехода от ламинарного к турбулентному режиму течения и обратно относительно хорошо действует для напорных потоков. При переходе к безнапорным потокам переходная зона между ламинарным и турбулентным режимами возрастает, и использование числа Рейнольдса как критерия не всегда правомерно.
Формула Пуазейля
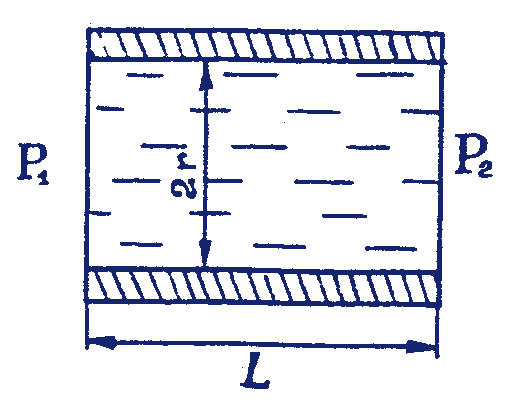Эта формула служит для количественного описания процессов ламинарного течения вязкой жидкости в цилиндрической трубе постоянного сечения, где V - объем вязкой жидкости, L- длина участка трубы, r - ее радиус, t - время истечения жидкости, (Р1 - Р2) - перепад давлений, h - вязкость.
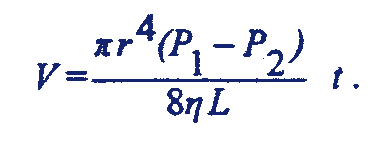
Разделив обе части этого выражения на время истечения t, слева получим объемную скорость течения жидкости Q. Величину 8hL / p r4 обозначим через X. Тогда формула Пуазейля принимает вид: 
Величина Q определяется в основном радиусом сосуда r. Это обусловлено главным образом тем, что кровоток пропорционален четвертой степени r, но так же и тем, что другие члены уравнения, например, разность давлений или длина для данного сосуда остается при обычных обстоятельствах примерно постоянной. Такая запись аналогична закону Ома для участка электрической цепи.
С помощью формулы Пуазейля можно определить ряд характеристик кровотока. Так, зная объемную скорость кровотока Q и величину гидравлического сопротивления сосудов, можно найти величину давления крови в любой точке сосудистой системы. Если Ро - давление крови в желудочке сердца, а X - общее сопротивление сосудов на участке сосудистой системы между желудочком и данной точкой, то давление крови Р в данной точке равно:
Р = Ро - QX.
Закон Пуазейля не используют для объяснения процессов, протекающих в сосудистой системе, так как кровеносные сосуды не имеют жестких стенок, а кровь не является вязкой гомогенной жидкостью, но он может быть полезен для понимания качественных закономерностей.
