Математический маятник.
Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.
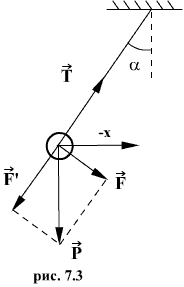
Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.7.3.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая 
, направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения 
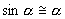и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна
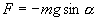
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
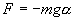
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
Момент силы относительно точки О: 
, и момент инерции:
M = FL.
Момент инерции J в данном случае
Угловое ускорение:
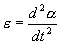
С учетом этих величин имеем:
или
| (7.8) |
Его решение
,
где  и 
| (7.9) |
Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.
Физический маятник.
Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.
При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.
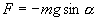
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
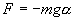
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
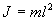. Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:
| (7.10) |
| (7.11) |
Решение этого уравнения
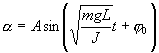
Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е.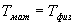 
или
.
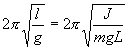Из этого соотношения определяем
Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.
