Работа и мощность при вращении твердого тела.
Найдем выражение для работы при вращении тела. Пусть сила 
приложена в точке 
, находящейся от оси 
на расстоянии 
, 
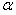— угол между направлением силы и радиус-вектором . Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол 
точка приложения проходит путь 
и работа равна произведению проекции силы на направление смещения на величину смещения:
.
Модуль момента силы равен:
,
тогда получим следующую формулу для вычисления работы:
.
Таким образом, работа при вращении твердого тела равна произведению момента действующей силы на угол поворота.
Кинетическая энергия вращающегося тела.
Моментом инерции мат.т. наз. физ. величина численно равная произведению массы мат.т. на квадрат расстояния этой точки до оси вращения.Wki =miV2i/2 Vi -Wri Wi=miw2r2i/2 =w2/2*miri2 Ii=mir2i момент инерции твердого тела равен сумме всех мат.т I=Simir2i моментом инерции твердого тела наз. физ.величина равная сумме произведений мат.т. на квадраты расстояний от этих точек до оси. Wi-IiW2/2 Wk=IW2/2
Wk =SiWki момент инерции при вращательном движении явл. аналогом массы при поступательном движении. I=mR2/2
21.Неинерциальные системы отсчёта. Силы инерции. Принцип эквивалентности. Уравнение движения в неинерциальных системах отсчёта.
Неинерциальная система отсчёта — произвольная система отсчёта, не являющаяся инерциальной. Примеры неинерциальных систем отсчета: система, движущаяся прямолинейно с постоянным ускорением, а также вращающаяся система.
При рассмотрении уравнений движения тела в неинерциальной системе отсчета необходимо учитывать дополнительные силы инерции. Законы Ньютона выполняются только в инерциальных системах отсчёта. Для того чтобы найти уравнение движения в неинерциальной системе отсчёта, нужно знать законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной.
Классическая механика постулирует следующие два принципа:
время абсолютно, то есть промежутки времени между любыми двумя событиями одинаковы во всех произвольно движущихся системах отсчёта;
пространство абсолютно, то есть расстояние между двумя любыми материальными точками одинаково во всех произвольно движущихся системах отсчёта.
Эти два принципа позволяют записывать уравнение движения материальной точки относительно любой неинерциальной системы отсчёта, в которой не выполняется Первый закон Ньютона.
Основное уравнение динамики относительного движения материальной точки имеет вид:
,
где 
— масса тела, 
— ускорение тела относительно неинерциальной системы отсчёта, 
— сумма всех внешних сил, действующих на тело, 
— переносное ускорение тела, 
— Кориолисово ускорение тела.
Это уравнение может быть записано в привычной форме Второго закона Ньютона, если ввести фиктивные силы инерции:
— переносная сила инерции
— сила Кориолиса
Сила инерции — фиктивная сила, которую можно ввести в неинерциальной системе отсчёта так, чтобы законы механики в ней совпадали с законами инерциальных систем.
В математических вычислениях введения этой силы происходит путём преобразования уравнения
F1+F2+…Fn = ma к виду
F1+F2+…Fn–ma = 0 Где Fi — реально действующая сила, а –ma — «сила инерции».
Среди сил инерции выделяют следующие:
простую силу инерции;
центробежную силу, объясняющую стремление тел улететь от центра во вращающихся системах отсчёта;
силу Кориолиса, объясняющую стремление тел сойти с радиуса при радиальном движении во вращающихся системах отсчёта;
С точки зрения общей теории относительности, гравитационные силы в любой точке — это силы инерции в данной точке искривлённого пространства Эйнштейна
Центробежная сила — сила инерции, которую вводят во вращающейся (неинерциальной) системе отсчёта (чтобы применять законы Ньютона, рассчитанные только на инерциальные СО) и которая направлена от оси вращения (отсюда и название).
Принцип эквивалентности сил гравитации и инерции — эвристический принцип, использованный Альбертом Эйнштейном при выводе общей теории относительности. Один из вариантов его изложения: «Силы гравитационного взаимодействия пропорциональны гравитационной массе тела, силы инерции же пропорциональны инертной массе тела. Если инертная и гравитационная массы равны, то невозможно отличить, какая сила действует на данное тело — гравитационная или сила инерции.»
Формулировка Эйнштейна
Исторически, принцип относительности был сформулирован Эйнштейном так:
Все явления в гравитационном поле происходят точно так же как в соответствующем поле сил инерции, если совпадают напряжённости этих полей и одинаковы начальные условия для тел системы.
22.Принцип относительности Галилея. Преобразования Галилея. Классическая теорема сложения скоростей. Инвариантность законов Ньютона в инерциальных системах отсчёта.
Принцип относительности Галилея – это принцип физического равноправия инерциальных систем отсчёта в классической механике, проявляющегося в том, что законы механики во всех таких системах одинаковы.
Математически принцип относительности Галилея выражает инвариантность (неизменность) уравнений механики относительно преобразований координат движущихся точек (и времени) при переходе от одной инерциальной системы к другой — преобразований Галилея.
Пусть имеются две инерциальные системы отсчёта, одну из которых, S, условимся считать покоящейся; вторая система, S', движется по отношению к S с постоянной скоростью u так, как показано на рисунке. Тогда преобразования Галилея для координат материальной точки в системах S и S' будут иметь вид:
x' = x - ut, у' = у, z' = z, t' = t (1)
(штрихованные величины относятся к системе S', нештрихованные — к S). Т. о., время в классической механике, как и расстояние между любыми фиксированными точками, считается одинаковым во всех системах отсчёта.
Из преобразований Галилея можно получить соотношения между скоростями движения точки и её ускорениями в обеих системах:
v' = v - u, (2)
a' = a.
В классической механике движение материальной точки определяется вторым законом Ньютона:
F = ma, (3)
где m — масса точки, a F — равнодействующая всех приложенных к ней сил.
При этом силы (и массы) являются в классической механике инвариантами, т. е. величинами, не изменяющимися при переходе от одной системы отсчёта к другой.
Поэтому при преобразованиях Галилея уравнение (3) не меняется.
Это и есть математическое выражение Галилеева принципа относительности.
ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ.
В кинематике все системы отсчета равноправны между собой и движение можно описывать в любой из них. При исследовании движений иногда приходится переходить от одной системы отсчета (с координатной системой ОХУZ) к другой - (О`Х`У`Z`). Рассмотрим случай, когда вторая система отсчета движется относительно первой равномерно и прямолинейно со скоростью V=соnst.
Для облегчения математического описания предположим, что соответствующие оси координат параллельны друг другу, что скорость направлена вдоль оси Х, и что в начальный момент времени (t=0) начала координат обеих систем совпадали друг с другом. Используя справедливое в классической физике допущение об одинаковом течении времени в обеих системах, можно записать соотношения, связывающие координаты некоторой точки А(х,у,z) и А (х`,у`,z`) в обеих системах. Такой переход от одной системы отсчета к другой носит название преобразований Галилея):
ОХУZ О`Х`У`Z`
t = t` t`= t
х = х` + Vxt х` = х - Vxt
y = y` y`= y
z = z` z` = z
x = v`x + Vx v`x = vx - Vx
ax = a`x a`x = ax
Ускорение в обеих системах одинаково (V=соnst). Глубокий смысл преобразований Галилея будет выяснен в динамике. Преобразование скоростей Галилея отражает имеющий место в классической физике принцип независимости перемещений.
Сложение скоростей в СТО
Классический закон сложения скоростей не может быть справедлив, т.к. он противоречит утверждению о постоянстве скорости света в вакууме. Если поезд движется со скоростью v и в вагоне в направлении движения поезда распространяется световая волна, то ее скорость относительна Земли все равно c, а не v + c.
Рассмотрим две системы отсчета.
В системе K 0 тело движется со скоростью v 1. Относительно же системы K оно движется со скоростью v 2. Согласно закону сложения скоростей в СТО: 
Если v << c и v 1 << c, то слагаемым 
можно пренебречь, и тогда получим классический закон сложения скоростей: v 2 = v 1 + v.
При v 1 = c скорость v 2 равна c, как этого требует второй постулат теории относительности: 
При v 1 = c и при v = c скорость v 2 вновь равна скорости c.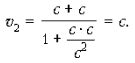 
Замечательным свойством закона сложения является то, что при любых скоростях v 1 и v (не больше c), результирующая скорость v 2 не превышает c. Скорость движения реальных тел больше, чем скорость света, невозможна.
Сложение скоростей
При рассмотрении сложного движения (то есть когда точка или тело движутся в одной системе отсчёта, а она движется относительно другой) возникает вопрос о связи скоростей в 2 системах отсчёта.
Классическая механика
В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:
Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы.
