Закон взаимосвязи массы и энергии. Кинетическая энергия в релятивистской динамике.

Для получения релятивистского выражения для кинетической энергии ис­пользуем её связь с работой силы, а силу подставим из релятивистской формы основного закона динамики материальной точки:

dЕ_к = dА = Fdr = (dР/dt)dr = u×d[(mu/Ö(l –u²/с²)] = u{d(mu)/Ö(l –u²/с²) + mu×dÖ(l –u²/с²)} = u{m×du/Ö(l - u²/с²) + m×u×(u/с²)×du/Ö(l –u²/с²)³} = m×u×du/Ö(l –u²/с²) + m×u³×(du/с²)/Ö(l –u²/с²)³ = [m×u×du - m×u³×(du/с²) + m×u³×(du/с²)]/Ö(l - u²/с²)³ = m×u×du/Ö(l –u²/с²)³ = d[mс²/Ö(l –u²/с²)] Þ
Е_к = mс²/Ö(l –u²/с²) + const;

При u = 0, Е_к = 0, то есть mс²/Ö(l –u²/с²) + const = 0, откуда const = - mс² и

Е_к = mс²/Ö(l –u²/с²) - mс² = mс²[(1/Ö(l –u²/с²) – 1].

При u << с, Ö(l –u²/с²)» 1 - u²/2с² и Е_к» mu²/2 переходит в известное из механики Ньютона выражение, справедливое при малых, дорелятивистских скоростях.

Кинетическая энергия, как энергия движения, предстает в виде разности энергий, одну
из которых естественно назвать полной энергией Е, а другую – E_о = mс² - энергией покоя:
Е_к = Е - Е_о.

Е = mс²/Ö(l - u²/с²) - полная энергия тела.

Из взаимосвязи массы m тела с энергией покоя Е_о = mс², следует, что всякое изменение Dm массы тела сопровождается изменением DЕ_о энергии покоя, так что DЕ_о = Dm×с² - закон взаимосвязи массы и энергии (покоя).

Энергия связи системы.

Масса образующейся составной частицы (системы) больше суммы масс ис­ходных частиц, т. к. кинетическая энергия соединяющихся частиц превращается в эквивалентное коли­чество энергии покоя. При обратном же процессе распада неподвижной частицы на составляю­щие её и разлетаю­щиеся в разные стороны частицы сумма масс образовавшихся частиц оказы­вается меньше массы исходной составной частицы на величину, равную сум­марной кинетиче­ской энергии разлетающихся частиц, деленной на с².

Связь частиц в составе более сложной частицы можно характеризовать энергией связи Е_св, численно равной работе, которую нужно затратить, чтобы преодолеть силы связи, разводя частицы на расстояние, где их вза­имодействие убывает до нуля:

Е_св = Sm_iс² - Мс², где М - масса системы. Здесь имеет место нарушение свойства аддитивности массы.

Соотношение между полной энергией и импульсом частицы.

Для установления взаимосвязи полной энергии с импульсом частицы, возве­дём её
в квадрат и разделим на с²:

Е = mс²/Ö(l –u²/с²) ® Е² – Е² u²/с² = m²с⁴ или, так как Р = mu/Ö(l –u²/с²) = Еu/с² Þ

Е² – Р²с² = m²с⁴ = const, или Е²/с² – Р² = m²с² = Inv

Энергия и импульс изменяются при переходе от одной ИСО к другой, но изменяются взаимосогласованно, образуя единую меру движения материи, на­зываемую комбинацией /тензором/ энергии - импульса. Подобно кинематическо­му инварианту - интервалу, объединив­шему в себе длину и длительность, тензор энергии - импульса образует динамический инвари­ант, объединяющий меры движения, сохранение которых тесно связано со свойствами симмет­рии пространства и времени – их однородностью.

Закон взаимосвязи массы и энергии

Полную энергию свободного тела можно определить как произведение его релятивистской массы на квадрат скорости света в вакууме:

 

 

27.Уравнение свободных колебаний без трения: пружинный маятник. Его решения. Вектор-амплитуда.

Пружинный маятник.

Колебательная система в этом случае представляет собой совокупность некоторого тела и прикрепленной к нему пружины. Пружина может располагаться либо вертикально (вертикальный пружинный маятник), либо горизонтально (горизонтальный пружинный маятник).
,где ах – ускорение, т - масса, х - смещение пружины, k – жесткость пружины.

Это уравнение называют уравнением свободных колебаний пружинного маятника.

Оно правильно описывает рассматриваемые колебания лишь тогда, когда выполнены следующие предположения:

1)силы трения, действующие на тело, пренебрежимо малы и поэтому их можно не учитывать;

2) деформации пружины в процессе колебаний тела невелики, так что можно их считать упругими и в соответствии с этим пользоваться законом Гука.

Свободные колебания пружинного маятника имеют следующие причины.

1. Действие на тело силы упругости, пропорциональной смещению тела х от положения равновесия и направленной всегда к этому положению.

2. Инертность колеблющегося тела, благодаря которой оно не останавливается в положении равновесия (когда сила упругости об­ращается в нуль), а продолжает двигаться в прежнем направлении.

Выражение для циклической частоты имеет вид:

,

где w - циклическая частота, k - жесткость пружины, т - масса.

Эта формула показывает, что частота свободных колебаний не зависит от начальных условий и полностью определяется собственными характеристиками самой колебательной системы — в данном случае жесткостью k и массой т.

Это выражение определяет период свободных колебаний пружинного маятника.

Пускай имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение).

Тогда второй закон Ньютона для рассматриваемой системы запишется так:

где F_c — сила сопротивления, F_y — сила упругости

F_c = − cv, F_y = − kx, то есть

ma + cv + kx = 0

или в дифференциальной форме

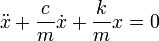
где k — коэффициент упругости в законе Гука, a — ускорение горизонтального движения грузика.

Для упрощения вводятся следующие обозначения:

Величину ω называют собственной частотой системы, ζ — коэффициентом затухания.

Тогда дифференциальное уравнение принимает вид

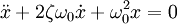
Сделав замену x = e ^{λ t} , получают характеристическое уравнение

Корни, которого вычисляются по следующей формуле

Зависимость графиков колебаний от значения ζ.

В зависисимости от величины коэффицинта затухания решение разделяется на три возможных варианта.

Апериодичность

Если , то имеется два действительных корня, и решение дифференциального уравнения принимает вид:

В этом случае колебания с самого начала экспоненциально затухают.

Граница периодичности

Если , два действительных корня совпадают , и решением уравнения является:

В данном случае может иметь место временный рост, но потом — экспоненциальное затухание.

Слабое затухание

Если , то решением характеристического уравнения являются два комплексно сопряжённых корня

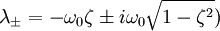
Тогда решением исходного дифференциального уравнения является

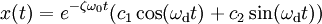
Где — собственная частота затухающих колебаний.

Константы c ₁ и c ₂ в каждом из случаев определяются из начальных условий: