Механическая энергия частицы в силовом поле
Сумму кинетической и потенциальной энергии - называют полной механической энергией частицы в поле:
| (5.30) |
Заметим, что полная механическая энергия Е, как и потенциальная, определяется с точностью до прибавления несущественной произвольной постоянной.
Консервативная система — физическая система, работа неконсервативных сил которой равна нулю и для которой имеет место закон сохранения механической энергии, то есть сумма кинетической энергии и потенциальной энергии системы постоянна.
Примером консервативной системы служит солнечная система. В земных условиях, где неизбежно наличие сил сопротивления (трения, сопротивления среды и др.), вызывающих убывание механической энергии и переход её в другие формы энергии, например в тепло, консервативная система осуществляются лишь грубо приближённо. Например, приближённо можно считать консервативной системой колеблющийся маятник, если пренебречь трением в оси подвеса и сопротивлением воздуха.
Диссипативная система — это открытая система, которая оперирует вдали от термодинамического равновесия. Иными словами, это устойчивое состояние, возникающее в неравновесной среде при условии диссипации (рассеивания) энергии, которая поступает извне. Диссипативная система иногда называется ещё стационарной открытой системой или неравновесной открытой системой.
Диссипативная система характеризуется спонтанным появлением сложной, зачастую хаотичной структуры. Отличительная особенность таких систем — несохранение объёма в фазовом пространстве, то есть не выполнение Теоремы Лиувилля.
Простым примером такой системы являются ячейки Бенара. В качестве более сложных примеров называются лазеры, реакция Белоусова — Жаботинского и сама биологическая жизнь.
Термин «диссипативная структура» введен Ильёй Пригожиным.
Закон сохранения энергии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что энергия изолированной (замкнутой) системы сохраняется во времени. Другими словами, энергия не может возникнуть из ничего и не может исчезнуть в никуда, она может только переходить из одной формы в другую. Закон сохранения энергии встречается в различных разделах физики и проявляется в сохранении различных видов энергии. Например, в термодинамике закон сохранения энергии называется первым началом термодинамики.
Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то правильнее называть его не законом, а принципом сохранения энергии.
Закон сохранения энергии является универсальным. Для каждой конкретной замкнутой системы, вне зависимости от её природы можно определить некую величину, называемую энергией, которая будет сохраняться во времени. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря, различающихся для разных систем.
Согласно теореме Нётер, закон сохранения энергии является следствием однородности времени.
W=Wk+Wп=const
14.Закон всемирного тяготения. Гравитационное поле и его характеристики. Потенциал поля. Связь между потенциалом и напряжённостью поля. Космические скорости.
Закон всемирного тяготения был открыт англичанином И. Ньютоном в 1666г. Закон звучит следующим образом: сила гравитационного притяжения двух материальных точек прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. В виде формулы это записывается так: F=G*m1*m2/r2 где G — гравитационная константа, определяемая экспериментально 6,67 × 10–11 Н·м2/кг2
ГРАВИТАЦИОННОЕ ПОЛЕ (поле тяготения), один из видов поля физического, посредством которого осуществляется гравитационное взаимодействие (притяжение) тел.
Гравитационное взаимодействие осуществляется через гравитационное поле. Всякое тело изменяет свойства окружающего его пространства — создает в нем гравитационное поле. Это поле проявляет себя в том, что помещенное в него другое тело оказывается под действием силы. Об «интенсивности» гравитационного поля, очевидно, можно судить по величине силы, действующей в данной точке на тело с массой, равной единице. В соответствии с этим величину называют Напряженностью гравитационного поля.
G=F/m
Величину φ=U/m’ называют потенциалом гравитационного поля. В этой формуле U есть потенциальная энергия, которой обладает материальная точка массы m’ в данной точке поля.
Потенциал – скалярная величина, поэтому пользоваться и вычислять φ проще, чем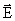 
.
Формулу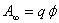 
можно использовать для установления единиц потенциала: за единицу φ принимают потенциал в такой точке поля, для перемещения в которую из бесконечности единичного положительного заряда необходимо совершить работу равную единице.
В физике часто используется единица энергии и работы, называемая электрон - вольт (эВ) – это работа, совершенная силами поля над зарядом, равным заряду электрона при прохождении им разности потенциалов 1 В.
Первая космическая скорость
Для осуществления равномерного движения по окружности радиуса r его горизонтально направленная скорость должна иметь такое значение v, при котором центростремительное ускорение равно ускорению свободного падения
(1).
Из (1) следует:
(2).
Скорость V, при которой тело может двигаться по круговой орбите вокруг Земли, называется первой космической скоростью.
Из формулы (2) для значения r, равного радиусу Земли, r = 6371 км, первая космическая скорость равна
V = 7.9*103 м/с
При начальной скорости меньше 7,9 км/с тело, брошенное горизонтально, пролетев некоторое расстояние, упадет на поверхность Земли. При скорости 7,9 км/с в отсутствии воздуха оно будет двигаться вокруг Земли по окружности, став ее искусственным спутником.
Вторая космическая скорость
При небольшом превышении первой космической скорости орбита спутника будет эллиптической, а при достижении скорости 11,2 км/с превращается в параболу, ветви которой уходят в бесконечность.
Скорость, при которой тело способно преодолеть действия сил притяжения небесного тела и удалиться от него на бесконечно далекое расстояние, называется второй космической скоростью.
Из формулы (2) следует, что для вычисления первой космической скорости на расстоянии r от любого небесного тела, звезды или планеты, нужно знать ускорения a свободного падения на этом расстоянии от центра масс небесного тела. Небесное тело массой M действует на другое тело массой m на расстоянии r силой всемирного тяготения F.
Следовательно, ускорение свободного падения тела на этом расстоянии равно
(3).
Из (2) и (3) первая космическая скорость V на расстоянии r от центра небесного тела массой M равна:
(4).
Формула (4) позволяет вычислять массы небесных тел, вокруг которых обращаются другие небесные тела под действием сил всемирного тяготения.
Массу M Солнца можно найти по известным значениям скорости V движениям Земли по ее орбите и радиусу r земной орбиты:
Скорость V движения Земли по орбите можно найти, зная радиус r земной орбиты и период Т ее обращения вокруг Солнца:
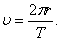
Для вычисления массы Солнца получаем формулу:
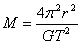(5).
Выразим период обращения Земли вокруг Солнца в единицах СИ:
T = 1 год = 3.16*107 с
Подставим числовые значения величин, найдем массу Солнца:
M = 2*1030 к
Из формулы (5) следует, что для всех спутников, обращающихся по круговым орбитам вокруг одной планеты, или для всех планет, обращающихся вокруг одной звезды, отношение квадратов периодов обращения к кубам радиусов орбит является величиной одинаковой
(6).
Равенство (6) выполняется и в случае движения спутников или планет по эллиптическим орбитам, если использовать как r большие полуоси эллипсов.
Третий закон Кеплера
Факт, что квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их эллиптических орбит, был открыт Иоганном Кеплером и называется третьим законом Кеплера:
(7).
