Пусть в замкнутой ограниченной пространственной области V, расположенной в декартовой прямоугольной системе координат Oxyz, определена непрерывная функция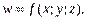 
Разобьем указанную область произвольным образом на элементарные области 
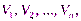объемы которых будем считать соответственно равными 
Внутри каждой элементарной области выберем произвольную точку 
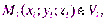
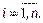
Диаметром области будем называть наибольшее из расстояний между любыми двумя точками границы области. Обозначим через 
диаметры элементарных областей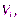 
а через 
– максимальный диаметр, т. е.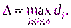 
Составим интегральную сумму функции f (x; y; z) в области V:
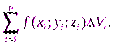
Устремим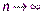 
так, чтобы 
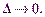Если существует предел интегральных сумм, который не зависит ни от способа разбиения области V на частичные области ни от выбора точек 
внутри каждой из этих областей, то этот предел называется тройным интегралом от функции f (x; y; z) по области V:
При этом говорят, что функция f (x; y; z) интегрируема в области V; x, y и z называют переменными интегрирования.
Достаточное условие интегрируемости функции: если определенная в некоторой ограниченной замкнутой области функция непрерывна, то она интегрируема в этой области.
Если функции f (x; y; z), f 1(x; y; z) и f 2(x; y; z) интегрируемы в области V, то имеют место следующие свойства:
1) линейность:
где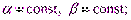 
2) аддитивность:
где 
и 
– области, не имеющие общих внутренних точек;
3) если выполняется неравенство 
то
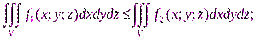
4) оценка модуля интеграла:
5) если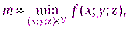 
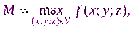то
где v – объем области V.
Геометрический смысл тройного интеграла:
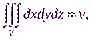(25.1)
где v – объем области V.
Вычисление тройных интегралов в декартовых координатах основано на понятии правильной пространственной области. Область V называют правильной в направлении оси Oz, если:
1) всякая прямая, проходящая через внутреннюю точку пространственной области V параллельно оси Oz, пересекает только один раз (только одну) «поверхность входа» и только один раз (только одну) «поверхность выхода»;
2) проекция D пространственной области V на плоскость xOy является правильной плоской областью в направлении оси Ox или Oy.
Пусть область V является правильной в направлении оси Oz, ограниченной снизу поверхностью 
а сверху – поверхностью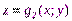 
(рис. 25.1). Пусть она проектируется на область 
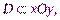элементарную в направлении оси Oy, и снизу ее ограничивает кривая 
а сверху – кривая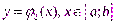 
(рис. 25.2).
Рис. 25.1
| 
Рис. 25.2
|
Тогда справедлива следующая формула:
(25.2)
причем интеграл в правой части равенства называется повторныминтегралом от функции f (x; y; z) по области V с внешним интегрированием по x, а 
– внутренним интегралом по переменной z.
Аналогично рассматривают пространственные области, правильные в направлении оси Ox или Oy, и применяют соответствующие формулы перехода к повторным интегралам.
Если область интегрирования V не подпадает под эти случаи, необходимо произвести разбиение этой области V на конечное число правильных областей и воспользоваться свойством аддитивности.
Пример 1. Вычислить тройной интеграл по области, ограниченной указанными поверхностями:
1) 
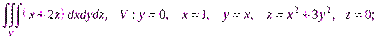
2) 
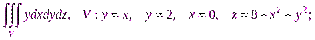
3) 
Решение. 1) Изобразим область интегрирования V (рис. 25.3).
Рис. 25.3
| Замечаем, что она является правильной в направлении оси Oz: снизу ее ограничивает плоскость 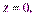 а сверху – поверхность эллиптического параболоида 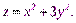 К тому же, область V проектируется на область плоскости xOy, которая является правильной областью в направлении оси Oy: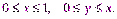 
Вычислим заданный интеграл, перейдя к повторному интегралу по формуле (25.2):
|
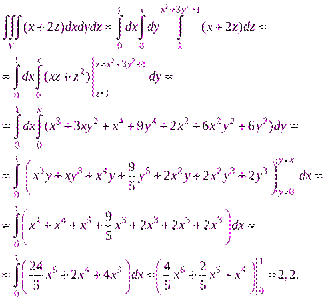
2) Нарисуем область интегрирования V (рис. 25.4).
Рис. 25.4
Расставим пределы интегрирования в декартовой системе координат, учитывая то, что она является правильной в направлении оси Oz:
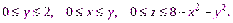
Вычислим данный интеграл, перейдя к повторному интегралу по формуле (25.2):
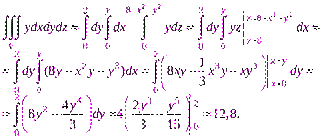
3) Изобразим область интегрирования V (рис. 25.5).
Рис. 25.5
Она является правильной в направлении оси Oz: 
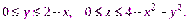
Перейдем к повторному интегралу по формуле (25.2) и вычислим данный интеграл:
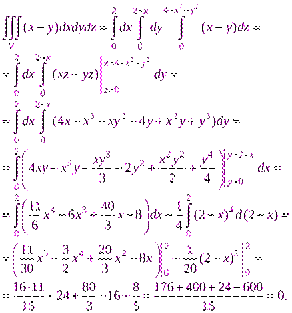
32. Тройные интегралы. Вычисление тройных интегралов в декартовой системе координат. Замена переменных в кратных интегралах Вычисление тройных интегралов в цилиндрической и сферической системах координат.
2. ТРОЙНЫЕ ИНТЕГРАЛЫ
2.1. Вычисление тройных интегралов вдекартовой системе координат
По аналогии с двойным интегралом вводится понятие тройного интеграла. Пусть в некоторой замкнутой ограниченной области T трехмерного пространства задана ограниченная функция трех переменных f (x,y,z). Разобьем эту область на n Dпроизвольных частей с объемами vi. В каждой частичной области возьмем произвольную точку M (xi,yi,zi) и составим сумму:
,
которая называется интегральной суммой для функции f(x,y,z) по области T. Если интегральная сумма при n (при этом диаметры всех областей должны стремится к нулю:¥®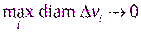 
) имеет предел, то этот предел называется тройным интегралом:
. (2.1)
Отметим, что тройные интегралы обладают свойствами, аналогичные свойствам двойных интегралов.
Перейдем теперь к вопросу о вычислении тройных интегралов в декартовой системе координат. Предположим, что область T является простой в направлении оси Oz, т.е. любая прямая, проведенная параллельно оси Oz, пересекает границу области T не более чем в двух точках. Это означает, что область T ограничена снизу поверхностью z=z 1(x,y), сверху поверхностью z=z 2(x,y) и с боков – цилиндрической поверхностью с образующими, параллельными оси Oz. Тогда по аналогии с формулой вычисления объемов цилиндрических тел при помощи двойных интегралов, можно получить
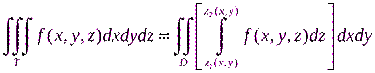. (2.2)
Здесь D проекция области T на плоскость xOy. Если область D является простой в направлении оси Oy, то можно написать
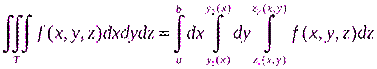. (2.3)
Отметим, что здесь внешний интеграл обязательно (!) должен иметь постоянные пределы (т.е. числа), пределы во втором интеграле могут зависеть только от той переменной, которая стоит во внешнем интеграле.
Если в тройном интеграле подынтегральная функция f(x,y,z 1, то тройной интеграл будет равен объему области интегрированияº) T, т.е.
