Функция  называется нормальной, если
называется нормальной, если
 .
.
Яндекс.Директ
Профподготовка учителя математики  bakalavr-magistr.ruЗаочно! Профподготовка для учителя математики 2017! Диплом. Выбирайте!Более 50 курсовВопросы и ответыСтоимостьДиплом bakalavr-magistr.ruЗаочно! Профподготовка для учителя математики 2017! Диплом. Выбирайте!Более 50 курсовВопросы и ответыСтоимостьДиплом
| Поможем с дипломной работой  piterdiplom.ruПомощь в написании дипломной работы от преподавателя ВУЗа.Узнай подробнее!ПсихологияПравоЭкономикаМенеджментАдрес и телефон piterdiplom.ruПомощь в написании дипломной работы от преподавателя ВУЗа.Узнай подробнее!ПсихологияПравоЭкономикаМенеджментАдрес и телефон
| Помощь с дипломнойи ВКРprofistudent.ruПомощь в написании дипломных работ. Антиплагиат от 80%! Доработки 0 руб.
|
Две функции  называются ортогональными (между собой), если
называются ортогональными (между собой), если  . Система кусочно-непрерывных на отрезке
. Система кусочно-непрерывных на отрезке  функций
функций
 (1)
(1)
(конечная или бесконечная) называется ортогональной, если функции имеют положительную норму и попарно ортогональны.
Система (1) называется ортогональной и нормальной (ортонормальной) или ортонормированной, если

т. е. она ортогональна и каждая входящая в нее функция имеет единичную норму.
Любая конечная ортогональная система функций  линейно независима в
линейно независима в  , т. е. из того, что
, т. е. из того, что
 ,
,
где  - числа, следует, что все
- числа, следует, что все  . В самом деле, если помножить обе части этого равенства скалярно на
. В самом деле, если помножить обе части этого равенства скалярно на  , то на основании линейных свойств скалярного произведения получим
, то на основании линейных свойств скалярного произведения получим
 ,
,
и так как  , то
, то 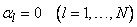 .
.
Если  - произвольная функция, то число
- произвольная функция, то число
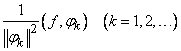
называется коэффициентом Фурье функции  относительно функции
относительно функции  , ортогональной системы (1). Ряд
, ортогональной системы (1). Ряд
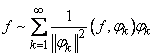 , (2)
, (2)
порождаемый функцией  , называется рядом Фурье функции
, называется рядом Фурье функции  по ортогональной системе (1).
по ортогональной системе (1).
Если система (1) ортонормальна, то  и ряд Фурье функции
и ряд Фурье функции  записывается еще проще:
записывается еще проще:
 . (3)
. (3)
Коэффициентами Фурье в этом случае являются числа  . В дальнейшем мы будем рассматривать только ортонормированные системы (1). Переход от них к произвольным ортогональным системам носит технический характер.
. В дальнейшем мы будем рассматривать только ортонормированные системы (1). Переход от них к произвольным ортогональным системам носит технический характер.
Теорема 1. Если система (1) ортонормирована, то для любой функции  норма
норма

среди всевозможных систем чисел 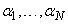 достигает своего минимума для единственной системы чисел, определяемых равенствами
достигает своего минимума для единственной системы чисел, определяемых равенствами
 ,
,
т. е. для коэффициентов Фурье функции  .
.
Таким образом,
 , (4)
, (4)
при этом
 . (5)
. (5)
Доказательство. Имеем

При этом очевидно, что последнее соотношение в этой цепи обращается в равенство только в единственном случае, когда  при любом
при любом 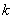 . Тем самым мы доказали соотношения (4) и (5).
. Тем самым мы доказали соотношения (4) и (5).
Из равенства (5), если учесть, что его левая часть есть неотрицательное число, вытекает неравенство
 ,
,
верное при любом  . Но тогда, если система (1) состоит из бесконечного числа функций
. Но тогда, если система (1) состоит из бесконечного числа функций  , то ряд, составленный из квадратов коэффициентов Фурье функции
, то ряд, составленный из квадратов коэффициентов Фурье функции  сходится и справедливо неравенство
сходится и справедливо неравенство
 , (6)
, (6)
называемое неравенством Бесселя.
Очень важен тот случай, когда ортонормированная система (1) такова, что неравенство (6) обращается в равенство (равенство Парсеваля-Стеклова)
 (7)
(7)
для всех функций  .
.
Чтобы выяснить значение равенства Парсеваля, зададим произвольную функцию  и составим для нее ее ряд Фурье
и составим для нее ее ряд Фурье
 .
.
Сумма первых  членов этого ряда
членов этого ряда

называется  -й суммой Фурье функции
-й суммой Фурье функции  по ортогональной системе (1).
по ортогональной системе (1).
Согласно формуле (5) отклонение  от
от  в смысле среднего квадратического (в смысле
в смысле среднего квадратического (в смысле  ) равно
) равно
 . (8)
. (8)
Если для функции  выполняется равенство Парсеваля (7), то
выполняется равенство Парсеваля (7), то
 , (9)
, (9)
и обратно, из (9) вытекает справедливость равенства Парсеваля (7).
Существует следующая терминология. Ортогональная система (1) называется полной в  , если ряд Фурьелюбой функции
, если ряд Фурьелюбой функции  сходится в смысле среднего квадратического к
сходится в смысле среднего квадратического к  , т. е. если имеет место свойство (9) для всех
, т. е. если имеет место свойство (9) для всех  .
.
Мы, таким образом, доказали, что для того чтобы ортонормированная система (1) была полной в  , необходимо и достаточно, чтобы для любой функции
, необходимо и достаточно, чтобы для любой функции  выполнялось равенство Парсеваля (7).
выполнялось равенство Парсеваля (7).
Примечание. Мы уже отмечали в замечании 1 §4.8, что  обозначает пространство функций
обозначает пространство функций  , интегрируемых в лебеговом смысле на
, интегрируемых в лебеговом смысле на  вместе со своими квадратами и что
вместе со своими квадратами и что  .
.
Рассмотрим ортонормированную на отрезке  систему непрерывных функций
систему непрерывных функций
 ,
,
полную в том, смысле, как это мы определили выше. Мы знаем, что если  , то для чисел
, то для чисел
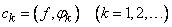 (10)
(10)
выполняется равенство Парсеваля
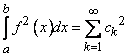 .
.
Это верно и для функций 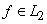 , только интегралы надо понимать в смысле Лебега.
, только интегралы надо понимать в смысле Лебега.
Но имеет место и обратное утверждение: если числа  таковы, что ряд
таковы, что ряд

сходится, то в  существует функция
существует функция  такая, что числа
такая, что числа  являются ее коэффициентами Фурье и выполняется соотношение (9).
являются ее коэффициентами Фурье и выполняется соотношение (9).
А в  такой функции может и не быть. В этом проявляется несовершенство пространства
такой функции может и не быть. В этом проявляется несовершенство пространства  . В пространстве
. В пространстве  недостаточно количество функций, для того чтобы это обратное утверждение имело место.
недостаточно количество функций, для того чтобы это обратное утверждение имело место.
25. Тригонометрической системой функций называется система функций
 Это – периодические функции.
Это – периодические функции.
Докажем два свойства периодических функций.
1) Если функция  имеет период
имеет период  , то функция
, то функция  имеет период
имеет период  .
.
Доказательство.  .
.
2) Если функция  имеет период
имеет период  , то
, то 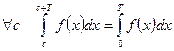 .
.
Доказательство.  =
=
(делаем замену переменных в последнем интеграле  )
)

 .
.
Доказанные свойства позволяют
1) рассматривать тригонометрическую систему функций на любом отрезке длиной  (период
(период  равен
равен  ,
,  ), например на отрезке
), например на отрезке  ,
,
2) при вычислениях интегралов от функций с периодом, кратным  , проводить интегрирование по любому отрезку длиной
, проводить интегрирование по любому отрезку длиной  .
.
Так как элементы тригонометрической системы функций представляют собой непрерывные функции, то они сами и их квадраты (как произведение непрерывных функций) интегрируемы на отрезке  . Поэтому можно рассматривать пространство L2 на отрезке
. Поэтому можно рассматривать пространство L2 на отрезке  и строить ряд Фурье.
и строить ряд Фурье.
Скалярное произведение функций введем так: 
Для того, чтобы построить ряд Фурье по тригонометрической системе функций надо доказать, что эти функции попарно ортогональны на  .
.
Теорема. Тригонометрическая система функцийсостоит из попарно ортогональных на отрезке  функций.
функций.
Доказательство.  .
.  ,
,
 ,
,
Пусть  .
.


Теорема доказана.
Вычислим скалярные квадраты элементов тригонометрической системы.
 ,
, 
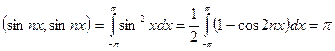 .
.
Составим ряд Фурье по тригонометрической системе функций
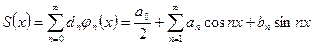 .
.
Коэффициенты Фурье вычисляются по формуле 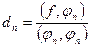 .
.
 ,
,  ,
,
 .
.
Теперь необходимо сформулировать условия, при которых функция представляется рядом Фурье по тригонометрической системе функций.




