Задание 1-20
Пример 1. 
Пример 2. 
Здесь применима теорема о пределе частного. К этому же выражению при х®  теорема о пределе неприменима, т. к.
теорема о пределе неприменима, т. к.  и
и  .
.
 представляет собой неопределенность вида
представляет собой неопределенность вида  .
.
Разложим на множители квадратный трехчлен.
9 х 2+8 х –1=9·(х –  )·(х +1).Для этого достаточно найти корни х 1 и х 2 квадратного трехчлена
)·(х +1).Для этого достаточно найти корни х 1 и х 2 квадратного трехчлена
ах 2+ bх + с = а (х – х 1)·(х – х 2).
Под знаком предела сократим одинаковые множители и перейдем к пределу:

Пример 3.  .
.
Обнаружив неопределенность 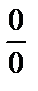 (так это в примере и записывают), раскладываем многочлены в числителе и в знаменателе на множители.
(так это в примере и записывают), раскладываем многочлены в числителе и в знаменателе на множители.
Сократив на х –1, получили дробь  , числитель которой стремится к конечному пределу, отличному от нуля (
, числитель которой стремится к конечному пределу, отличному от нуля (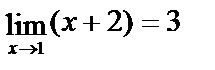 ), а знаменатель при х ®1 является бесконечно малой, тогда дробь при х®1 является бесконечно большой.
), а знаменатель при х ®1 является бесконечно малой, тогда дробь при х®1 является бесконечно большой.
Пример 4.  .
.
Решение. Здесь числитель и знаменатель не имеют конечных пределов, имеем неопределенность  . Поделив одновременно числитель и знаменатель на х 3, получим
. Поделив одновременно числитель и знаменатель на х 3, получим
 , т. к. каждая из дробей
, т. к. каждая из дробей  является бесконечно малой и стремится к нулю.
является бесконечно малой и стремится к нулю.
Пример 5. 
Решение.
 , так как
, так как
 .
.
Для раскрытия неопределенности  следует числитель и знаменатель разделить на одну и ту же старшую степень переменной.
следует числитель и знаменатель разделить на одну и ту же старшую степень переменной.
Пример 6. 
Решение.

В этом примере нужно было избавиться от радикалов, для чего умножили и числитель и знаменатель на сумму – сопряженное числителю выражение. Применив формулу разности квадратов в числителе, мы избавились от радикалов:
 .
.
Задание 21-40. Найти производные функций.
Пример 1: 
Решение: 


 +
+

 .
.
При вычислении производной использовали правило и формулы дифференцирования: 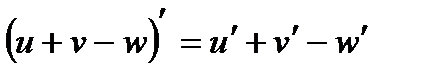 ;
;  ;
;  ;
; 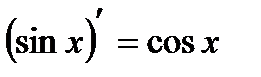 ;
;  .
.
Пример 2: 
Решение:

При вычислении производной использовали правила и формулы дифференцирования:
 ;
; 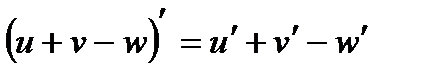 ;
;  ;
;  ;
;  .
.
Пример 3: 
Решение: вычислим производную сложной степенной функции, применив формулу дифференцирования 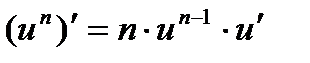 , получим
, получим
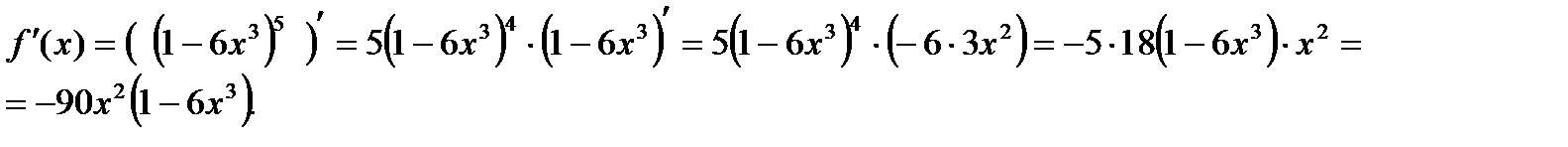
Пример 4: 
Решение: вычислим производную сложной тригонометрической функции, применив формулу дифференцирования  , получим
, получим

Задание 41-60: Исследовать функцию и построить ее график
Пример: Исследовать функцию и построить ее график:
 .
.
Решение:
1) Функция определена на всей числовой оси, т. е. ее область определения  .
.
2) Найдем точки пересечения с осями координат:
с осью ОХ: решим уравнение 
 .
.
с осью ОY: 
3) Выясним, не является ли функция четной или нечет
ной:
 .
.
Отсюда следует, что функция является нечетной.
4) Функция непериодическая.
5) Найдем промежутки монотонности и точки экстремума функции: 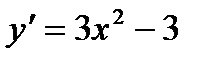 .
.
Критические точки:  .
.

| 
| -1 | 
| 1 | 
|

| + | 0 | - | 0 | + |

| т. max | т. min -2 |

6) Найдем промежутки выпуклости и точки перегиба функции: 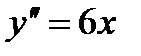
Критические точки:  .
.

| 
| 0 | 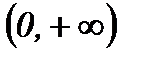
|

| - | 0 | + |

| точка перегиба |

7) Функция непрерывна, асимптот у нее нет.
По результатам исследования построим график функции:
Задание 61-80. Найти неопределенные интегралы и вычислить определенный интеграл:
Пример 1 а) Найти неопределенный интеграл:
 .
.
Решение: 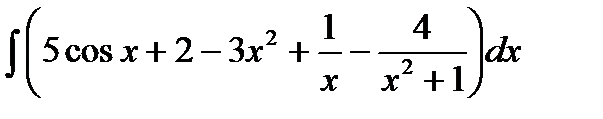 =
=
= 



 .
.
б) Найти неопределенный интеграл:  .
.
Решение:  =
= 

 .
.
в) Найти неопределенный интеграл 
Решение:  =
= 

Пример 2. а) Найти неопределенный интеграл 
Решение:  =
= 





б) Найти неопределенный интеграл 
Решение: 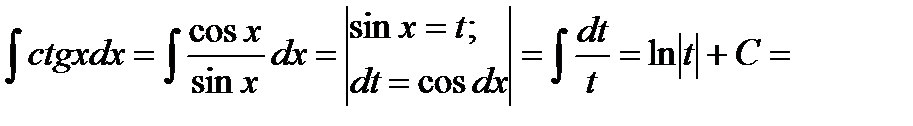
= 
в) Найти неопределенный интеграл 
Решение:  =
= 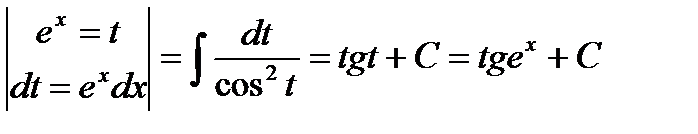
г) Найти неопределенный интеграл 
Решение: 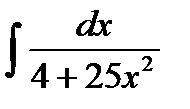 =
= 
=  =
=  .
.
Пример 3 а) Вычислить определенный интеграл методом замены переменной 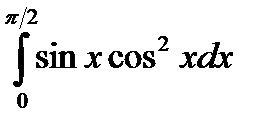
Решение:  =
= 
 .
.
б) Вычислить определенный интеграл:  .
.
Решение: 

 .
.
Задание 81-100. Сделать чертеж и с помощью определенного интеграла вычислить:
Пример 1. Найти площадь фигуры, ограниченной линиями:
 .
.
Решение. Площадь данной фигуры равна разности площадей криволинейных трапеций, образованных прямой  и гиперболой
и гиперболой 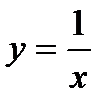 на отрезке
на отрезке 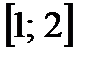 .
.
 .
.
Пример 2. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.
Решение. Используем формулу для нахождения объёма тел вращения:  .
.
 .
.
Таблица производных основных элементарных и сложных функций
х- независимая переменная, u=u(x)-дифференцируемая функция
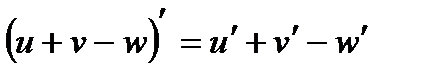




1.1.  1.2.
1.2.  1.3.
1.3.  1.4
1.4  1.5.
1.5.  1.6
1.6  1.7
1.7  1.8
1.8  1.9
1.9  1.10
1.10  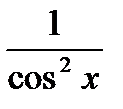 1.11
1.11   1.12
1.12  1.13
1.13  1.14
1.14  1.15
1.15 
|
2.2  2.3
2.3  2.4
2.4  2.5
2.5 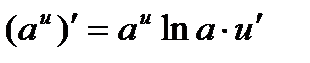 2.6
2.6   2.7
2.7 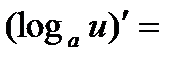 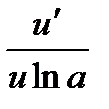 2.8
2.8 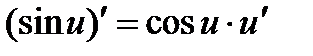 2.9
2.9  2.10
2.10   2.11
2.11   2.12
2.12  2.13
2.13  2.14
2.14  2.15
2.15 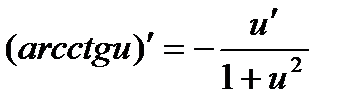
|
Таблица интегралов
1.  2.
2.  3.
3. 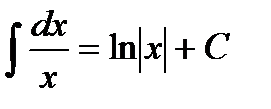 6.
6.  7.
7. 


 

|
4.  5.
5.  8.
8.  9.
9. 



  
|


Контрольная работа
«Основы математического анализа»
Задание 1-20. Вычислить пределы функций:
1. а)  б)
б)  в)
в) 
2. а)  б)
б)  в)
в) 
3. а)  б)
б)  в)
в) 
4. а)  б)
б) 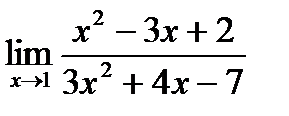 в)
в) 
5. а)  б)
б)  в)
в) 
6. а)  б)
б)  в)
в) 
7. а)  б)
б)  в)
в) 
8. а)  б)
б)  в)
в) 
9. а)  б)
б)  в)
в) 
10. а) 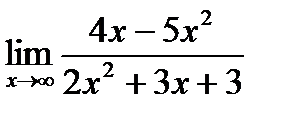 б)
б)  в)
в) 
11. а) 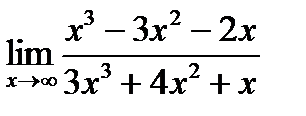 б)
б)  в)
в) 
12. а) 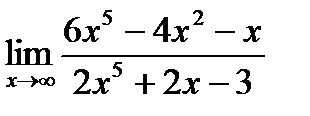 б)
б)  в)
в) 
13. а) 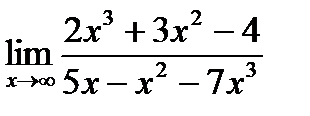 б)
б) 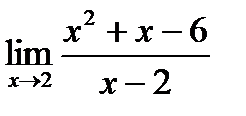 в)
в) 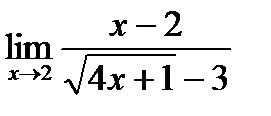
14. а)  б)
б)  в)
в) 
15. а)  б)
б)  в)
в) 
16. а)  б)
б)  в)
в) 
17. а)  б)
б)  в)
в) 
18. а)  б)
б) 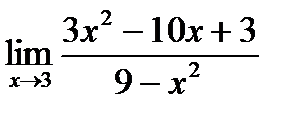 в)
в) 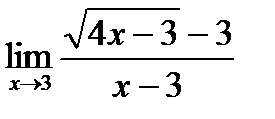
19. а)  б)
б)  в)
в) 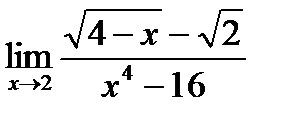
20. а)  б)
б)  в)
в) 
Задание 21-40. Найти производные функций.
21. а)  , б)
, б)  , в)
, в) 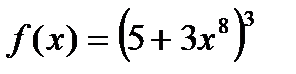 , г)
, г)  .
.
22. а)  , б)
, б)  , в)
, в)  ,
,
г)  .
.
23. а)  , б)
, б)  , в)
, в)  , г)
, г)  .
.
24. а)  , б)
, б)  , в)
, в)  , г)
, г)  .
.
25. а) 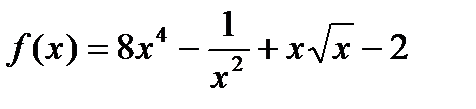 , б)
, б)  , в)
, в)  , г)
, г)  .
.
26. а)  , б)
, б)  , в)
, в)  ,
,
г) 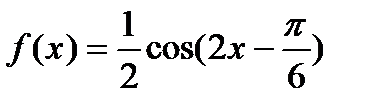 .
.
27. а)  , б)
, б) 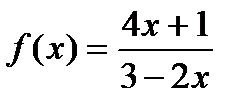 , в)
, в)  , г)
, г)  .
.
28. а)  , б)
, б)  , в)
, в)  ,
,
г).  .
.
29. а)  , б)
, б)  , в)
, в)  , г)
, г)  .
.
30. а)  , б)
, б)  , в)
, в)  , г)
, г)  .
.
31. а)  , б)
, б)  , в)
, в)  , г)
, г)  .
.
32. а)  , б)
, б)  , в)
, в)  ,
,
г)  .
.
33. а)  , б)
, б)  , в)
, в)  , г)
, г)  .
.
34. а)  , б)
, б)  , в)
, в)  ,
,
г)  .
.
35. а)  , б)
, б)  , в)
, в)  , г)
, г) 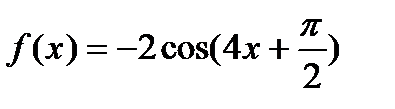 .
.
36. а)  , б)
, б)  , в)
, в)  ,
,
г)  .
.
37. а)  , б)
, б)  , в)
, в)  , г)
, г)  .
.
38. а)  , б)
, б) 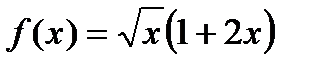 , в)
, в)  ,
,
г)  .
.
39. а)  , б)
, б)  , в)
, в)  , г)
, г)  .
.
40. а)  , б)
, б)  , в)
, в) 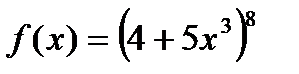 ,
,
г)  .
.
Задание 41-60: Исследовать функцию и построить ее график:
61.  62.
62. 
63.  64.
64. 
65. 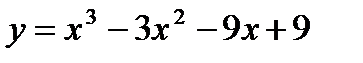 66.
66. 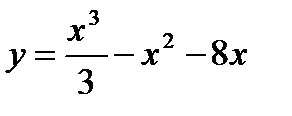
67.  68.
68. 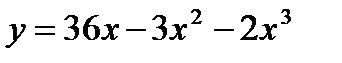
69. 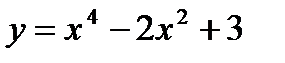 70.
70. 
71.  72.
72. 
73.  74.
74. 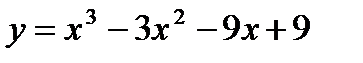
75.  76.
76. 
77.  78.
78. 
79.  80.
80. 
Задание 61-80. Найти неопределенные интегралы и вычислить определенный интеграл:
61. а) 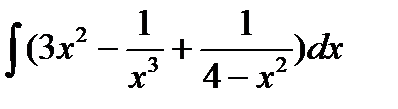 б)
б)  в)
в) 
62. а)  б)
б)  в)
в) 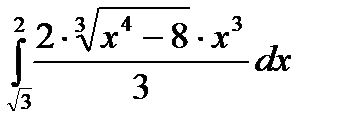
63. а)  б)
б)  в)
в) 
64. а)  б)
б)  в)
в) 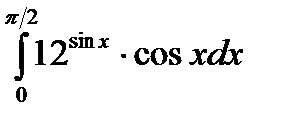
65. а)  б)
б)  в)
в) 
66. а)  б)
б)  в)
в) 
67. а)  б)
б)  в)
в) 
68. а)  б)
б) 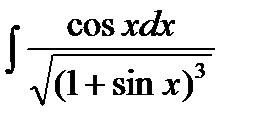 в)
в) 
69. а) 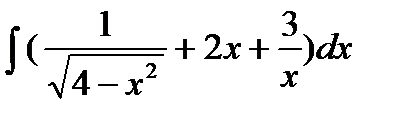 б)
б)  в)
в) 
70. а)  б)
б)  в)
в) 
71. а)  б)
б)  в)
в) 
72. а) 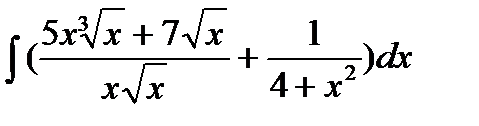 б)
б) 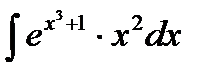 в)
в) 
73. а)  б)
б)  в)
в) 
74. а)  б)
б)  в)
в) 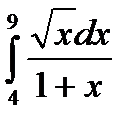
75. а)  б)
б)  в)
в) 
76. а)  б)
б)  в)
в) 
77. а)  б)
б)  в)
в) 
78. а)  б)
б)  в)
в) 
79. а)  б)
б) 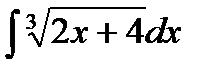 в)
в) 
80. а)  б)
б)  в)
в) 
Задание 81-100. Сделать чертеж и с помощью определенного интеграла
- Вычислить площадь фигуры, ограниченной данными линиями
 ;
; - Вычислить площадь фигуры, ограниченной данными линиями

- Вычислить площадь фигуры, ограниченной данными линиями

- Вычислить площадь фигуры, ограниченной данными линиями

- Вычислить площадь фигуры, ограниченной данными линиями
 .
. - Вычислить площадь фигуры, ограниченной данными линиями
 .
. - Вычислить площадь фигуры, ограниченной данными линиями
 .
. - Вычислить площадь фигуры, ограниченной данными линиями
 .
. - Вычислить площадь фигуры, ограниченной данными линиями
 .
. - Вычислить площадь фигуры, ограниченной данными линиями

- Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной данными линиями
 .
. - Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной данными линиями
 .
. - Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной данными линиями
 .
. - Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной данными линиями.

- Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной данными линиями.

- Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной данными линиями.
- Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной данными линиями.
- Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной данными линиями.
- Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной данными линиями.
- Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной данными линиями.






