Производной функции 
по аргументу x называется предел отношения ее приращения 
к приращению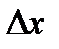 
аргумента x, когда приращение аргумента стремится к нулю: 
.
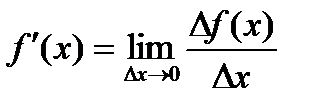Если этот предел конечный, то функция y=f(x) называется дифференцируемой в точке x. Если же этот предел есть ∞, то говорят, что функция y=f(x) имеет в точке x бесконечную производную.
Механический смысл производной: скорость есть первая производная пути по времени, т.е. 
.
Геометрический смысл производной: тангенс угла наклона касательной к графику функции 
равен первой производной этой функции, вычисленной в точке касания, т.е.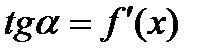 
Уравнение касательной к графику функции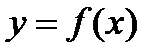 
в точке 
:
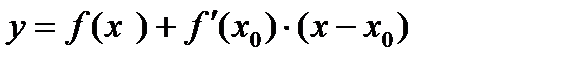
Уравнение нормали к графику функции 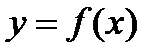в точке :
Пусть y= y(u), где u= u(x) – дифференцируемые функции. Тогда сложная функция y=y[u(x)] есть также дифференцируемая функция, причем 
, или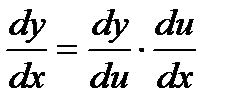 
Это правило распространяется на цепочку из любого конечного числа дифференцируемых функций: производная сложной функции равна произведению производных функций, ее составляющих.
Производная второго порядка (вторая производная) от функции y=f(x) есть производная от ее первой производной: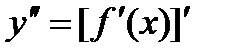 
.
Производная третьего порядка (третья производная) от функции y=f(x) есть производная от ее второй производной: 
.
Производная n-ого порядка(n -я производная) от функции y=f(x) есть производная от ее (n-1)-й производной: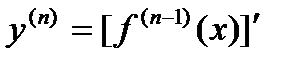 
.
Исследование функции с помощью производной
Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство:
.
Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство:
.
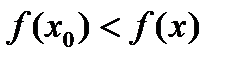Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Точками экстремума могут служить только критические точки I рода, т.е. точки, принадлежащие области определения функции, в которых производная 
обращается в нуль или терпит разрыв.
Правило нахождения экстремумов функции 
с помощью первой производной
1. Найти производную функции .
2. Найти критические точки по первой производной, т.е. точки, в которых производная обращается в нуль или терпит разрыв.
3. Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции 
. Если на промежутке 
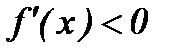, то на этом промежутке функция убывает; если на промежутке 
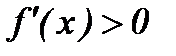, то на этом промежутке функция возрастает.
4. Если в окрестности критической точки меняет знак
с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.
5. Вычислить значения функции в точках минимума и максимума.
С помощью приведенного алгоритма можно найти не только экстремумы функции, но и промежутки возрастания и убывания функции.
Правило нахождения экстремумов функции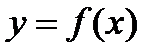 
с помощью второй производной
1. Найти производную 
.
2. Найти стационарные точки данной функции, т.е. точки, в которых 
.
3. Найти вторую производную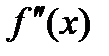 
.
4. Исследовать знак второй производной в каждой из стационарных точек. Если при этом вторая производнаяокажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то – минимум. Если же вторая производная равна нулю, то экстремум функции надо искать с помощью первой производной.
5. Вычислить значения функции в точках экстремума.
Направление выпуклости графика функции. Точки перегиба
Кривая 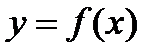называется выпуклой вниз в промежутке 
, если она лежит выше касательной в любой точке этого промежутка.
Кривая 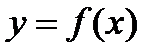называется выпуклой вверх в промежутке , если она лежит ниже касательной в любой точке этого промежутка.
Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Выпуклость вниз или вверх кривой, являющейся графиком функции 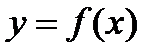, характеризуется знаком ее второй производной: если в некотором промежутке 
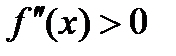, то кривая выпукла вниз на этом промежутке; если же 
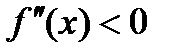, то кривая выпукла вверх на этом промежутке.
Точка графика функции 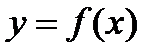, разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.
Точками перегиба могут служить только критические точки II рода, т.е. точки, принадлежащие области определения функции 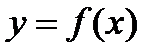, в которых вторая производная 
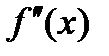обращается в нуль или терпит разрыв.
Правило нахождения точек перегиба графика функции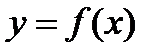 
1. Найти вторую производную .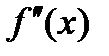
2. Найти критические точки II рода функции 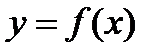, т.е. точки, в которой 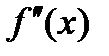обращается в нуль или терпит разрыв.
3. Исследовать знак второй производной 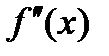в промежутка, на которые найденные критические точки делят область определения функции 
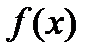. Если при этом критическая точка 
разделяет промежутки выпуклости противоположных направлений, то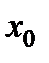 
является абсциссой точки перегиба графика функции.
4. Вычислить значения функции в точках перегиба.
Общая схема для построения графиков функций
1. Найти область определения функции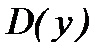 
.
2. Найти точки пересечения графика функций с осями координат.
3. Исследовать функцию на четность или нечетность.
4. Исследовать функцию на периодичность.
5. Найти промежутки монотонности и точки экстремума функции.
6. Найти промежутки выпуклости и точки перегиба функции.
7. Найти асимптоты функции.
По результатам исследования построить график
Контрольные вопросы:
1. Дать определение производной функции.
2. Что называется приращением аргумента, приращением функции?
3. Какой механический смысл имеет производная?
4. Сформулировать геометрический смысл производной.
5. Как найти производную суммы или разности?
6. Как найти производную произведения?
7. Как найти производную частного двух функций?
8. Дать определение дифференциала функции.
9. Сформулируйте правила нахождения производной сложной функции?
10. Как найти производную второго порядка? производную четвертого порядка.
11. Что такое критические точки функции?
12. Сформулировать достаточные условия возрастания и убывания функции.
13. Какими точками отделяются промежутки возрастания от промежутков убывания функции?
14. Сформулируйте правила нахождения точек экстремума функции.
15. Сформулировать достаточное условие выпуклости функции. Приведите алгоритм нахождения промежутков выпуклости и точек перегиба
