Момент инерции – характеристика инерциальных свойств при вращательном движении. Характеризует распределение массы относительно оси вращения.
– это точки
(это не «зе» английская, а знак такой).
Осевые моменты инерции некоторых тел:
Шар –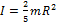 
, ось сплошного цилиндра 
, ось полого цилиндра - 
, прямой тонкий стержень -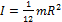 
.
Теорема Штейнера – Для того, чтобы найти момент инерции относительно произвольной оси нужно сложить момент инерции этого телаотносительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела на квадрат расстояния между осями.
Уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
Момент силы определяет скорость изменения момента импульса.
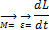
Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точки О в точку А приложения силы, на силу F:
Здесь М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F. Модуль момента силы
(18.1)
где a— угол между r и F; r sina = l — кратчайшее расстояние между линией действия силы и точкой О — плечо силы.
Моментом силы относительно неподвижной оси z называется скалярная величина Mz, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z. Значение момента Мz не зависит от выбора положения точки О на оси z.
(18.3)
Уравнение (18.3) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
Закон сохранения момента импульса.
В замкнутых системах моментов импульса отдельных частей с течением времени не изменяются.
(над всеми L нужен вектор «стрелка»).
В замкнутой системе момент внешних сил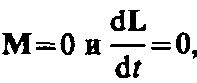 
Здесь мы продемонстрируем закон сохранения момента импульса с помощью скамьи Жуковского. Человек, сидящий на скамье, вращающаяся вокруг вертикальной оси, и держащий в вытянутых руках гантели (рис. 2), вращается внешним механизмом с угловой скоростью ω1. Если человек прижмет гантели к телу, то момент инерции системы уменьшится. Но момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость вращения ω2 увеличивается. Аналогичным образом, гимнаст во время прыжка через голову поджимает к туловищу руки и ноги, с целью уменьшить свой момент инерции и тем самым увеличить угловую скорость вращения.
