Пусть в некоторой области 3-х мерного пространства задано скалярное поле 
. Выберем в этой области точку 
. Если перемещаться из этой точки вдоль какой-либо линии, то поле будет меняться от точки к точке. Причем, ясно, что для различных направлений скорость изменения 
также может оказаться различной и должна характеризовать само поле в рассматриваемой точке или ее окрестности. При этом, по смыслу рассуждений, эта величина должна быть векторной. Рассмотрим строгое определение этой характеристики на примере гидромеханической аналогии. Пусть в пространстве задано скалярное поле давления жидкости или газа. Поместим в эту область тело произвольной формы, ограниченное поверхностью 
, (рис. 24). Вычислим суммарую силу 
, действующую на тело со стороны среды.
Рис.24 К определению градиента скалярной функции
Рассмотрим площадку 
, содержащую точку на поверхности . Модуль силы, действующей на площадку , равен 
, а направление совпадает с направлением нормали к поверхности в точке . Таким образом, вектор силы
| (71) |
Полная сила может быть вычислена интегрированием по поверхности :
| (72) |
Если результат (72) разделить на объем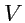 
, заключенный внутри поверхности , то получившаяся величина
| (73) |
будет "средней" силой, действующей со стороны среды на любую точку внутри . Физической причиной этого действия является перепад давлений между различными точками среды.
Способность поля (в данном случае поля давлений) оказывать действие на пробное тело является характеристикой самого поля и поэтому не должна зависеть на формы и размеров тела, помещенного в это поле. Будем стягивать поверхность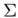 
к точке 
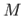, таким образом, 
и рассмотрим предел
| (74) |
Если предел (74) существует, то по смыслу рассуждений он определит плотность силы, действующей со стороны поля (давлений) на точечное тело, помещенное в точку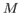 
и будет характеризовать быстроту изменения поля (перепад давлений) в окрестности этой точки.
Рассмотрим общий случай скалярного поля 
. Если для поля существует предел (74) при стягивании поверхности к точке 
, то он называется градиентом поля 
в этой точке:
| (75) |
По определению 
является вектором и вообще, выражение (75), будучи примененным в каждой точке области определения поля 
, будет задавать векторное поле градиента .
Формула (75) задает определение 
в форме, независящей от системы координат - инвариантно. Пользуясь (75), получим формулу вычисления градиента скалярного поля в декартовой системе координат. Тогда, так как вектор нормали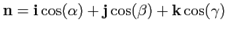 
:
| (76) |
Применим к каждому слагаемому (76) формулу Остроградского-Гаусса (3.1):
| (77) |
Применяя теорему о среднем к правой части (77), получим
| (78) |
переходя к пределу 
и сравнивая с определением градиента (75), получим формулу для вычисления градиента в декартовой системе координат:
| (79) |
Производная по направлению скалярное поле некоторое направление с помощью единичного вектора 
. вектор определяет координатную ось 
и пользуясь правилом дифференцирования сложной функции, вычислим производную
| (80) |
Полученное выражение, учитывая, что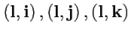 
- координаты вектора 
,можно переписать как скалярное произведение
| (81) |
Это выражение (81) называется производной по направлению 
поля .
Из определения (81) следуют свойства градиента:
1. 
направлен перпендикулярно к линии уровня 
;
2. 
направлен в сторону наискорейшего возрастания функции ;
Формула (79) позволяет получить следующие свойства и правила вычисления 
:
1. 
| 
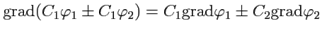
| (82) |
| 2.
| 
| (83) |
| 3.
|  (сложное поле) 
| (84) |
Пример 3-8. Вычислить градиент поля 
, где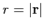 
- модуль радиус-вектора, 
.
Решение. Согласно выражению (79), получим
Аналогично, 
, 
и тогда, складывая вычисленные производные, получим:
или в бескоординатной форме 
