1°. Случай одной независимой переменной. Если z=f(x,y) есть дифференцируемая
функция аргументов х и у, которые в свою очередь являются дифференцируемыми
функциями независимой переменной t: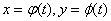 
, то производная
сложной функции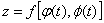 
может быть вычислена по формуле
 .
| (1) |
В частности, если t совпадает с одним из аргументов, например х, то "полная"
производная функции z по х будет:
 .
| (2) |
Пример. Найти 
, если 
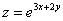, где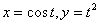 
.
Решение. По формуле (1) имеем:
Пример. Найти частную производную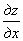 
и полную производную , если 
.
Решение. 
.
На основании формулы (2) получаем 
.
2 °. Случай нескольких независимых переменных.
Пусть z = f(x;y) — функция двух переменных х и у, каждая из которых является функцией
независимой переменной t: х = x(t), у = y(t). В этом случае функция z=f(x(t);y(t)) является
сложной функцией одной независимой переменной t; переменные х и у — промежуточные переменные.
Теорема. Если z == f (x; у) — дифференцируемая в точке М(х;у) 
D функция
и х = x(t) и у = y(t) — дифференцируемые функции независимой переменной t,
то производная сложной функции z(t) == f (x(t);y(t)) вычисляется по формуле
| (3) |
Частный случай: z = f(x; у), где у = у(х), т.е. z = f(x;y(x)) — сложная функция одной
независимой переменной х. Этот случай сводится к предыдущему, причем роль переменной
t играет х. Согласно формуле (3) имеем:
или
.
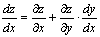Последняя формула носит название формулы полной производной.
Общий случай: z = f(x;y), где х = x(u;v), y=y(u;v). Тогда z = f{x(u;v);y(u;v)) — сложная
функция независимых переменных и и v. Ее частные производные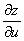 
и 
можно найти,
используя формулу (3) следующим образом. Зафиксировав v, заменяем в ней 
, 
соответствующими частными производными 
| (4) |
Аналогично получаем:
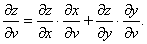
| (5) |
Таким образом, производная сложной функции (z) по каждой независимой переменной (и и v)
равна сумме произведений частных производных этой функции (z) по ее промежуточным
переменным (x и у) на их производные по соответствующей независимой переменной (u и v).
Во всех рассмотренных случаях справедлива формула
(свойство инвариантности полного дифференциала).
Пример. Найти 
и 
, если z= f (x,y), где x=uv, 
.
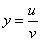Решение. Применяя формулы (4) и (5), получим:
Пример. Показать, что функция 
удовлетворяет уравнению 
.
Решение. Функция 
зависит от х и у через промежуточный аргумент 
, поэтому
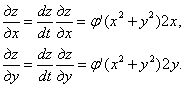
Подставив частные производные в левую часть уравнения, будем иметь:
, т. е. функция z удовлетворяет данному уравнению.
Формула градиента
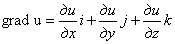
Вопрос. Производная неявной функции (Рассмотреть случаи одной и нескольких независимых переменных).Примеры
