(Определение, область определения, область значений, график, линии уровня).Примеры
| Функции нескольких переменных |
| 1. Функция двух переменных и ее область определения |
Определение. Переменная  называется функцией двух переменных называется функцией двух переменных  и и  , если:
1) задано множество , если:
1) задано множество  пар численных значений пар численных значений  и и  ;
2) задан закон, по которому каждой паре чисел ;
2) задан закон, по которому каждой паре чисел  из этого множества соответствует единственное численное значение.
При этом переменные из этого множества соответствует единственное численное значение.
При этом переменные  и и  называются аргументами или независимыми переменными. Обозначения функций двух переменных аналогичны обозначениям функций одной переменной: называются аргументами или независимыми переменными. Обозначения функций двух переменных аналогичны обозначениям функций одной переменной:
 , ,  , , 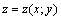 , , 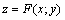 и т.д.
При нахождении частного значения и т.д.
При нахождении частного значения 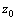 функции функции  , которое она принимает при заданных значениях аргументов , которое она принимает при заданных значениях аргументов  и и  , пишут , пишут 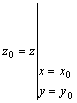 или или  .
Определение. Множество .
Определение. Множество  всех пар значений аргументов данной функции двух переменных называется областью определения этой функции.
Например, областью определения функции всех пар значений аргументов данной функции двух переменных называется областью определения этой функции.
Например, областью определения функции 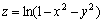 является множество, для которого является множество, для которого  . Множество . Множество  таких точек образует внутренность круга с центром в начале координат и радиусом, равным единице.
Графиком функции двух переменных в прямоугольной декартовой системе координат в пространстве является в общем случае поверхность.
Линией уровня функции таких точек образует внутренность круга с центром в начале координат и радиусом, равным единице.
Графиком функции двух переменных в прямоугольной декартовой системе координат в пространстве является в общем случае поверхность.
Линией уровня функции  называется линия называется линия 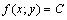 на плоскости на плоскости  , в точках которой функция сохраняет постоянное значение , в точках которой функция сохраняет постоянное значение  .
Аналогично .
Аналогично  функция трех переменных. функция трех переменных.
|
Определение. Пусть имеется п переменных величин, и каждому набору их значений (хх, х2,..., хп) из некоторого множества X соответствует одно вполне определенное значение переменной величины z. Тогда говорят, что задана функция нескольких переменныхz=f(хх, х2,..., хп).
Переменные хх, х2,..., хп называются независимыми переменными или аргументами, z — зависимой переменной, а символ f означает закон соответствия. Множество X называется областью определения функции. Очевидно, это подмножество n-мерного пространства.

Функцию двух переменных обозначают z=f(x, у). Тогда ее область определения X есть подмножество координатной плоскости Оху.
Окрестностью точки  называется круг, содержащий точку
называется круг, содержащий точку  (см. рис. 1).
(см. рис. 1).
Очевидно, круг на плоскости есть двумерный аналог интервала на прямой.
При изучении функций нескольких переменных используется математический аппарат: любой функции z=f(x, у) можно поставить в соответствие пару функций одной переменной: при фиксированном значении х=х0 функцию z=  и при фиксированном значении у=у0 функцию z=f(x, у0).
и при фиксированном значении у=у0 функцию z=f(x, у0).
Графиком функции двух переменных z=  называется множество точек трехмерного пространства (х, у, z), аппликата z которых связана с абсциссой х и ординатой у функциональным соотношением z=
называется множество точек трехмерного пространства (х, у, z), аппликата z которых связана с абсциссой х и ординатой у функциональным соотношением z=  .
.
Для построения графика функции z=f(x, у) полезно рассматривать функции одной переменной z=f(x, у0) и z=  , представляющие сечения графика z=f(x, у) плоскостями, параллельными координатным плоскостям Oxz и Oyz, т.е. плоскостями у= у0 и х=х0.
, представляющие сечения графика z=f(x, у) плоскостями, параллельными координатным плоскостям Oxz и Oyz, т.е. плоскостями у= у0 и х=х0.

Пример 1. Построить график функции  .
.
Решение. Сечения поверхности  =
=  плоскостями, параллельными координатным плоскостям Oyz и Oxz, представляют параболы (например, при х = 0
плоскостями, параллельными координатным плоскостям Oyz и Oxz, представляют параболы (например, при х = 0  , при у = 1
, при у = 1  и т.д.). В сечении поверхности кординатной плоскостью Оху, т.е. плоскостью z=0, получается окружность
и т.д.). В сечении поверхности кординатной плоскостью Оху, т.е. плоскостью z=0, получается окружность  График функции представляет поверхность, называемую параболоидом (см. рис. 2)
График функции представляет поверхность, называемую параболоидом (см. рис. 2)
Определение. Линией уровня функции двух переменных z=f{x, у) называется множество точек на плоскости, таких, что во всех этих точках значение функции одно и то же и равно С. Число С в этом случае называется уровнем.
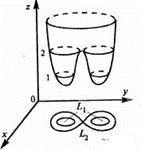
На рис.3 изображены линии уровня, соответствующие значениям С=1 и С=2. Как видно, линия уровня  состоит из двух непересекающихся кривых. Линия
состоит из двух непересекающихся кривых. Линия  – самопересекающаяся кривая.
– самопересекающаяся кривая.
Многие примеры линий уровня хорошо известны и привычны. Например, параллели и меридианы на глобусе — это линии уровня функций широты и долготы. Синоптики публикуют карты с изображением изотерм — линий уровня температуры.

Пример 2. Построить линии уровня функции  .
.
Решение. Линия уровня z=C это кривая на плоскости Оху, задаваемая уравнением х2 + у2 - 2 у = С или х2 + (у - I)2 = С+1. Это уравнение окружности с центром в точке (0; 1) и радиусом 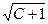 (рис. 4).
(рис. 4).
Точка (0; 1) — это вырожденная линия уровня, соответствующая минимальному значению функции z=-1 и достигающемуся в точке (0; 1). Линии уровня — концентрические окружности, радиус которых увеличивается с ростом z=C, причем расстояния между линиями с одинаковым шагом уровня уменьшаются по мере удаления от центра. Линии уровня позволяют представить график данной функции, который был ранее построен на рис. 2.






