Закон распределения случайной величины определяют согласно известным критериям проверки статистических гипотез Персона (χ2), Мизеса (ω2). Причем, когда идет речь о выборке данных небольшого объема (до 100 значений) рекомендуется проверять гипотезу о законе распределения случайной величины согласно критерию Мізеса (ω2), в противном случае –. Персона (χ2).
В основе отмеченных критериев лежит сравнение (приглаживание) эмпирической и теоретической функции распределения.
Эмпирическая функция распределения имеет вид ступенчатой ломаной линии. Эмпирическая функция распределения может быть построена за вариационным рядом полученной реализации случайной величины из соотношения:
,
где: 
– полученные реализации случайной величины T, образующие вариационный ряд.
Построив эмпирическую функцию распределения, высказывается нулевая гипотеза о законе распреледения случайной величины Т.
Неизвестный закон подбирается исходя из вида эмпирической функции распределения и потом проверяется на согласие с помощью разных критериев.
Критерий ω2 Мизеса. В качестве меры отклонения эмпирической функции распределения Qn*(t) от гипотетической Q(t) принята среднеквадратичная метрика, то есть средний квадрат отклонений по всем возможным значениями аргумента (4). Решение (4) для ступенчатой функции распределения можно записать в виде соотношения:
(9)
Из (9) видно, что данный критерий учитывает индивидуальные члены выборки. На практике предлагается использовать следующую формулу для определения статистики:
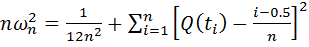, (10)
где: Q(ti) – значение гипотетической функции распределения при 
. Полученное значение статистики (10) сравнивается с критическим значением nωn 2(α), табл. 1 (значение статистики nωn2 совпадает из значения статистики критерия Андерсена). Если 
, то гипотеза Н 0 принимается, в пртивном случае – отклоняется.
Критерий χ2 К.Пирсона. Данный критерий часто применяется на практике статистических исследований. Результаты статистических испытаний n значений исходной выборки случайной величины Т разбиваются на k интервалов Δ1, Δ2,.. Δn и получают статистический ряд в виде представленном в табл. 3.
Таблица 2
Статистический ряд разбивки выборки по ячейкам
| Δ i | x1; x2;x3 | x4; x5;x6 | … | xn-2; xn-1;xn |
| pi* | pi* | pi* | … | pi* |
Зная теоретический (гипотетический) закон распределения Q(ti), находят теоретические вероятности попадания случайной величины Т в каждый из интервалов р 1, р 2,.. рn при этом их сумма должна равняться единице. Проверка согласованности теоретического и статистического распределений заключается в проверке расхождений между теоретическими вероятностями рі и полученными частотами. Как меру расхождения целесообразно принять сумму квадратов отклонения (рі *– рі), взятых с некоторыми взвешивающими коэффициентами С и. К Пирсон предложил как взвешивающие коэффициенты принять величину
.
При таком выборе коэффициентов Сi мера расхождения будет
, (11)
где: 
– частота появления событий в і -ом интервале;
n i – число значений величины Т, которые попали в i -й интервал;
n – общее число значений в выборке t 1, t 2,.. t n.
Статистика (11) практически не зависит от функции распределения Q(t) и от объема выборки n, а зависит только от числа разрядов (интервалов) k, и с увеличением n закон распределения этой статистики приближается к распределению χ 2 из r = k -1 степенью свободы, для которого есть специальные таблицы.
Для проверки исходной гипотезы Н 0 при заданном или избранном уровне значимости α полученная статистика (11) сравнивается с критическим значением χr2(α) и если χ2 < χr2(α), то принимается гипотеза о согласии теоретического и статистического законов распределения, если же χ2 > χr2(α), то гипотеза Н 0 отклоняется.
Данный критерий применяется при большом объеме выборки и при числе реализаций в интервале не менее 5-10. При таких условиях вероятность β ошибки второго рода будет минимальной.
К изъянам критерия χ 2 стоит отнести произвольность распределения данных на разряды и потерю информации при группировке выходных данных/
Как при использовании критерия Мизеса, так и при использовании критерия К. Персона стоит задача оценки параметров неизвестного (гипотетического) распределения. В общем случае предлагается применять для решения этой задачи метод максимального правдоподобия.
2 КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется выборкой, вариационным рядом. Какие требования относятся к выборке?
2 Доложить порядок статистической обработки информации по надежности;
3 Что называется уровнем значимости?
4 Для чего применяется критерий Андерсена?
5 Критерий К.Пирсона и Мизеса: условия применения, преимущества и недостатки этих критериев.
6. Методика построения гистограммы.
7. Формирование гипотезы о распределении ошибок и проверка ее истинности
