Подготовка экспериментальных данных

Подготовка экспериментальных данных о точности выполняется в следующей последовательности:

1 Из результатов измерений, бланк измерений, таблица 1 выбираются и заносятся на страницу Excel значения измеренных значений широты и долготы по каждой точке отдельно (из значений выбираются только десятые доли минут. Определяются выборочные значение математического ожидания широты и долготы по каждой точке отдельно. Синтаксис определения: =СРЗНАЧ(E5:E14), Е2:Е14 – границы выборки.

Далее определяется ошибка измерений широты и долготы для каждого измерения. Синтаксис =E$5-C5. E$5 – ячейка, в которой хранится среднее значение широты или долготы соответственно; C5 – ячейка, в которой хранится первое значение измеренных значений. Далее эта формула распространяется на все значения измерений.

Часто случается, что выходных данных для получения представительской выборки не хватает, тогда, если имеются данные измерений координат по другим точкам, может быть высказана и проверенна гипотеза о принадлежности двух выборок к одной генеральной совокупности. Такая гипотеза может быть проверена с помощью критерия Андерсона:

, (6)

где i, и j – порядковые номера значений y _i и х_j в своих выборках;

r_i и s_j – порядковые номера значений y _i и х_j в общем вариационном ряду;

m, n – объемы первой и второй выборки.

При конечных значениях m и n рекомендуется вместо статистики (6) использовать более простую в пользовании статистику

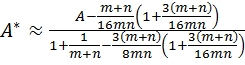(7)

Для проверки исходной гипотезы Н₀ полученная статистика А сравнивается с критическим значением статистики А(α), представленным в таблице 2 в зависимости от уровня значимости

Таблица 2

Критические значения статистика А

Если вычислена по формулам 6 или 7 статистика А окажется меньше критической А (α) из табл. 2 то есть А< А (α), то гипотеза Н ₀ принимается; если же окажется, что А≥ А (α), то исходная гипотеза Н₀ об однородности исследуемых выборок, отбрасывается, то есть выборки считаем неоднородными.

При подтверждении нулевой гипотезы выборки объединяют.

Выборочные характеристики несут значительную информацию о возможном законе распределения случайной величины. Например, при равенстве среднего, моды и медианы можно допустить, что случайная величина распределена по нормальному закону, в противном случае и при равенстве коэффициента эксцесса ≈6, а коэффициента асимметрии ≈2 можно допустить, что мы имеем дело с показательным распределением и так далее. Вид гистограммы или полигона частот также несет информацию о возможном законе распределения.

Никаких специальных средств в MathCAD и Excel для проверки гипотезы об однородности выборки нет.

Excel предлагает кроме того две функции ZТЕСТ и ФТЕСТ.

Функция ZТЕСТ возвращает двустороннее P –значение z –теста. Z –тест определяет стандартную оценку для X относительно массива данных и возвращает двустороннюю вероятность для нормального распределения. Можно использовать эту функцию, чтобы оценить вероятность того, что конкретное наблюдение взято из конкретной генеральной совокупности.

Синтаксис: ZТЕСТ (массив;X;сигма), где: массив – интервал данных, с которыми сравнивается одиночное наблюдение Х; X – значение, которое проверяется; cигма – известное стандартное отклонение генеральной совокупности. Если этот параметр опущен, то используется стандартное отклонение выборки.

Функция ФТЕСТ возвращает результат F –тестa. F –тест возвращает одностороннюю вероятность того, что дисперсии аргументов масив1 и масив2 различаются несущественно. Эта функция используется для того, чтобы определить, имеют ли две выборки разные дисперсии.

Синтаксис ФТЕСТ(масив1;масив2), где: Масив1 – первый массив или интервал данных, Масив2 – второй массив или интервал данных.

Если исходные выборки достаточно большие (не менее 50 значений) и выборочные характеристики несущественно отличаются, то данный тест может быть применен для проверки гипотезы об однородности выборок.

Проверка по критерию Андерсена частных выборок и объединение всех частных выборок в одну генеральную выборку выполняется по всем точкам.