Лабораторная работа № 1.
ИССЛЕДОВАНИЕ ТОЧНОСТИ ОПРЕДЕЛЕНИЯ МЕСТА ОБЪЕКТА
ПО ДАННЫМ СИСТЕМЫ СРНС
Цель: 1.Выработать у студентов практических навыков в проведении измерений координат места и определения точности измерений.
2. Освоить методы обработки статистических данных и методики статистических измерений.
Лабораторное оборудование:
1.Приемник GPS типа etrex, другие GPS приемники.
2. Персональный компьютер с необходимым программным обеспечением.
Предварительные замечания
Прежде, чем приступить к работе, необходимо повторить теорию вероятностей, в частности математическую статистику. В общем случае, обработка полученных результатов измерений сводится к определению моментных характеристик случайных измерений:
– математического ожидания случайной величины;
– среднеквадратического отклонения и дисперсии;
– построения гистограммы частостей и определения закона распределения случайной величины;
Методика проведения обработки результатов измерений приводятся в приложении к заданию.
Порядок проведения измерений
В качестве точек привязки выбираем:
– точка № 1 – юго-западный угол здания УК;
– точка № 2 – вход в здание ЛК- 1;
– точка № 3 – вход в студенческий корпус;
– точка № 4 – памятник П.С. Нахимову.
– точка № 5 – вход в здание ВЦ.
Студенты поочередно перемещаются от точки к точке, производят измерения и заносят их в бланк, форма бланка – таблица 1. Для обеспечения заданной достоверности измерений количество измерений уточняется в процессе выполнения работы.
После набора необходимой статистической выборки (не менее 50 отсчетов) – производится обработка статистических данных и определение ошибок и точного значения координат выбранных точек.
Таблица 1
Форма бланка измерений
| № | Широта | Долгота | Точность | № | Широта | Долгота | Точность |
Основные сведения из теории
Методы статистической обработки информации
Методы статистической обработки информации разделяются на три группы.
К первой группе методов можно отнести самые простые вычисления средних значений случайной величины за период наблюдения. В этом случае исследователя интересует лишь фактическое среднее значение, оценка достоверности его расчета не всегда обязательна.
Ко второй группе относятся методы расчетов выборочных характеристик случайной величины (в нашем случае координат точек, в которых проводятся измерения, если известны все измеренные случайные величины (координаты) Х 1, Х 2, Х 3, Х 4..., Хn, точек. При этом должна быть получена оценка достоверности и точности расчета среднего значения. Для оценки вероятности и точности вычисления стоит применять законы распределения, что обычно и вызывает наибольшие трудности.
К третьей, наиболее сложной группе относятся методы определения распределения вероятностей случайных величин.
Некоторые термины и определения:
Множественное число результатов, полученное при проведении наблюдений (измерений) называется выборкой.
Упорядоченная по росту выборка (ранжированная выборка) называется статистическим рядом.
Число наблюдений, которые образуют выборку, называется объемои выборки N.
К статистической информации относятся следующие требования:
– показательность;
– достоверность;
– однородность.
Как известно, случайная величина (координаты точек, ошибки измерений) полностью описывается законом ее распределения. Если вид закона распределения и его параметры известны, то легко определить любую характеристику случайной величины. Поэтому статистическая обработка информации о результатах измерений, как правило, сводится к определению вида закона распределения (точности определения координат) и его параметров.
Статистическое определение закона распределения случайной величины всегда было связано с большими объемами вычислений, однако современные средства математических вычислений напр. MathCAD, Excel, Statistica и др. позволяют автоматизировать и значительно облегчить этот процесс. Техническая сторона этого вопроса хорошо описана в специальной и учебной литературе, посвященной испытаниям и статистическим исследованиям. Основной упор делается на применение пакетов MathCAD и Excel для проведения соответствующих расчетов. В данной лабораторной работе рекомендуется применение пакета Excel.
В ряде случаев вид закона распределения времени безотказной работы известен, тогда задача сводится к оценке параметров закона распределения с применением известных методик.
В результате испытаний можно получить точечные значения оценки параметра и интервальные оценки. При интервальных оценках определяется, какой интервал оценок с заданной доверительной вероятностью β накрывает математическое ожидание оцениваемого параметра. Границы такого интервала называются доверительными границами. Можно записать:
 , (1)
, (1)
где  и
и  – нижняя и верхняя доверительные границы параметра Θ.
– нижняя и верхняя доверительные границы параметра Θ.
Вероятность того, что значение Θ выйдет из интервала [  ], называют уровнем значимости α
], называют уровнем значимости α
 (2)
(2)
Наиболее часто значения доверительных вероятностей принимают ровными 0,90; 0,95; 0,99 или уровни значимости соответственно 0,10; 0,05; 0,01.
Доверительная вероятность α, обусловлена соотношением (1), характеризует степень вероятности результатов двусторонней (то есть с определением двух границ) оценки. Но часто в практических целях достаточно установить одну из границ интервала, нижнюю или верхнюю, что отвечают доверительным вероятностям β 1, или β 2. Тогда:


Вероятности β 1, β 2и β связаны между собой уравнением:
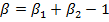
Но, чаще всего, вид закона случайной величины заранее не известен. Тогда необходимо проводить весь комплекс статистических расчетов по сглаживанию экспериментальных данных наиболее пригодным (приемлемым) законом распределения и подбор (вычисление) его параметров.
Рассмотрим последовательность действий при определении вида закона распределения.
Наиболее распространенными законами распределения случайной величины в ошибок являются:
– нормальный,
–усеченный нормальный;
– Релея;
– гамма.
Поэтому при определении вида закона распределения рекомендуется аппроксимировать экспериментальные характеристики данными законами в данной последовательности.
При определении закона распределения целесообразно придерживаться следующего порядка:
– подготовка данных (ошибок измерения координат);
– определение выборочных характеристик;
– построение гистограммы ошибок;
– проверка допустимости гипотетического закона распределения ошибок, используя определенные критерии согласия:
χ2 К. Пирсона:
 , (3)
, (3)
ω2 Мизеса:
 (4)
(4)
Дп Колмогорова:
 и др. (5)
и др. (5)






