. Функция 
непрерывна на отрезке 
если:
1) она непрерывна на интервале 
;
2) непрерывна в точке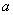 
справа и в точке 
слева.
Функция 
непрерывна в точке 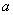справа, если она определена в данной точке и её правосторонний предел совпадает со значением функции в данной точке: 
. Она непрерывна в точке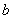 
слева, если определена в данной точке и её левосторонний предел равен значению: 
Вторая теореме Вейерштрасса, непрерывная на отрезке 
функция достигает своей точной верхней грани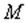 
и своей точной нижней грани 
.
Число 
также называют максимальным значением функции на отрезке и обозначают через 
, а число 
– минимальным значением функции на отрезке с пометкой 
.
В нашем случае:
.
Грубо говоря, наибольшее значение находится там, где самая высокая точка графика, а наименьшее – где самая низкая точка.
Важно! Как уже заострялось внимание в статье об экстремумах функции, наибольшее значение функции и наименьшее значение функции – НЕ ТО ЖЕ САМОЕ, что максимум функции и минимум функции. Так, в рассматриваемом примере число 
является минимумом функции, но не минимальным значением.
Кстати, а что происходит вне отрезка 
? Да хоть потоп, в контексте рассматриваемой задачи это нас совершенно не интересует. Задание предполагает лишь нахождение двух чисел 
и всё!
Пример 1
Найти наибольшее и наименьшее значения функции 
на отрезке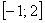 
Вопрос.Выпуклость и вогнутость прямой. Примеры.
Выпуклость функции, точки перегиба
График функции 
, дифференцируемой на интервале 
, является на этом интервале выпуклым, если график этой функции в пределах интервала лежит не выше любой своей касательной (рис. 1).
График функции , дифференцируемой на интервале , является на этом интервале вогнутым, если график этой функции в пределах интервала лежит не ниже любой своей касательной (рис. 2).
Теоремы о выпуклости функции и точках перегиба
Теорема
(Об условиях выпуклости или вогнутости графика функции)
Пусть функция 
определена на интервале 
и имеет непрерывную, не равную нулю в точке 
вторую производную. Тогда, если 
всюду на интервале 
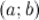, то функция имеет вогнутость на этом интервале, если 
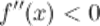, то функция имеет выпуклость.
Определение
Точкой перегиба графика функции 
называется точка 
, разделяющая промежутки выпуклости и вогнутости.
Теорема
(О необходимом условии существования точки перегиба)
Если функция имеет перегиб в точке , то 
или не существует.
Теорема
(О достаточном условии существования точки перегиба)
Если:
1. первая производная 
непрерывна в окрестности точки 
;
2. вторая производная 
или не существует в точке 
;
3. 
при переходе через точку 
меняет свой знак,
тогда в точке 
функция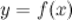 
имеет перегиб.
