Определение
При вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределенностями.
Основные виды неопределенностей: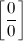 
, 
, 
, 
, 
, 
, 
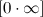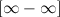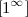Все другие выражения не являются неопределенностями и принимают какое-то конкретное конечное или бесконечное значение.
Основные пределы
1. Первый замечательный предел: 
Пример
Задание. Вычислить предел 
Решение. Получим неопределенность, сделаем замену. При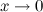 
: 
, 
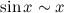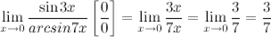
Ответ. 
Задание. Найти предел 
Решение. 
Ответ. 
4. Предел целой рациональной функции: если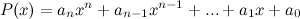 
, то 
Вопрос.Условия монотонности дифференцируемой функции. Примеры.
Монотонность функции и ее связь с производной
Монотонность функции, основные понятия и определения
Определение
Функция 
называется строго возрастающей на промежутке
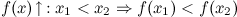
Пример
Функция 
является возрастающей на промежутке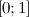 
, так как:
для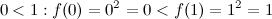 
Определение
Функция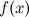 
называется строго убывающей на промежутке,
Пример
Функция является строго убывающей на промежутке 
, так как:
для 
Функция строго возрастающая или строго убывающая на промежутке называется монотонной на этом промежутке.
Определение
Функция называется неубывающей на промежутке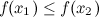 
.
Функция называется невозрастающей на промежутке, 
.
Связь монотонности функции с ее производной
Теорема
(Об условии возрастания/убывания монотонной функции)
Если производная функции 
на некотором промежутке 
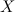, то функция возрастает на этом промежутке; если же 
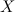на промежутке , то функция убывает на этом промежутке.
Замечание
Если функция возрастает на промежутке, то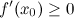 
или не существует.
Пример
Задание. Исследовать функцию 
на монотонность на всей числовой прямой.
Решение. Найдем производную заданной функции:
Для любого действительного 
: 
, функция возрастает на всей действительной оси.
Ответ. Функция возрастает на всей действительной оси.
Вопрос. Экстремумы функций (необходимые и достаточные условия существования) экстремума. Примеры
Понятие экстремума функции
Определение
точка локального максимума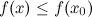 
.
точка локального минимума 
.
Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума - локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.
, строгое неравенство 
.
строгого локального минимума строгое неравенство 
.
Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.
Замечание
Необходимое условие экстремума
Теорема
(Необходимое условие экстремума)
Если функция имеет экстремум в точке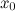 
, то ее производная 
либо равна нулю, либо не существует.
-называются стационарными точками функции.
Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки - это либо стационарные точки (решения уравнения ), либо это точки, в которых производная 
не существует.
Замечание
Не в каждой своей критической точке функция обязательно имеет максимум или минимум.
