Дифференциал функции
Пусть функция 
дифференцируема в точке 
, то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно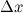 
и нелинейного членов:
где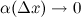 
при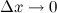 
.
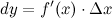
Замечание
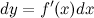
Геометрический смысл дифференциала
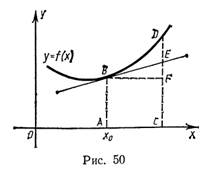На рис. 50 изображен график некоторой дифференцируемой функции f (х) в окрестности точки х0.
Выражения ∆x, f (х0), f(х0+∆х) и ∆f=f(х0+∆х)-f(х0) геометрически означают соответственно длины
|
Инвариантность формы записи
Инвариантность формы записи дифференциалов первого порядка
Пример
Инвариантность формы записи дифференциалов второго порядка
Однако, уже для второго порядка, это не верно: 
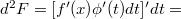
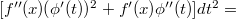
Упс! Инвариантности нет.
Формула Лейбница
. 
где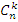 
- биномиальные коэффициенты:
Эта формула доказывается по индукции аналогично биномиальным коэффициентам.
11.Вопрос.Основные теоремы о дифференциалах. Таблица дифференциалов.
Основные теоремы дифференциального исчисления
Теорема Ферма
Теорема
Теорема Ферма. (О равенстве нулю производной)
Тогда производная в этой точке равна нулю, то есть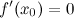 
.
Следствие. (Геометрический смысл теоремы Ферма)
В точке наибольшего и наименьшего значения, достигаемого внутри промежутка, касательная к графику функции параллельна оси абсцисс.
Теорема Ролля
Теорема
Теорема Ролля. (О нуле производной функции, принимающей на концах отрезка равные значения)
1. 
.
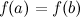Тогда на интервале 
найдется, по крайней мере, одна точка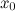 
, в которой .
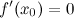Следствие. (Геометрический смысл теоремы Ролля)
Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс.
Следствие.
Если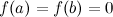 
, то теорему Ролля можно сформулировать следующим образом: между двумя последовательными нулями дифференцируемой функции имеется, хотя бы один, нуль производной.
Теорема Лагранжа
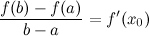
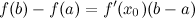
Теорема Коши
Таблица дифференциалов
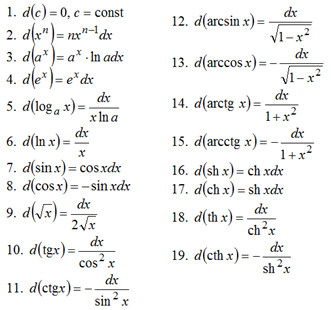
12.Вопрос.Применение дифференциалов в приближённых вычислениях значений функций. Дифференциалы высших порядков.Примеры.
Применение дифференциала в приближенных вычислениях формулы:
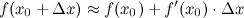
Дифференциалы высших порядков
Дифференциал второго порядка обозначается следующим образом:
Аналогично определяются дифференциалы более высоких порядков.
Определение
Дифференциалом 
-го порядка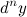 
функции называется дифференциал от дифференциала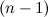 
-го порядка этой функции, то есть
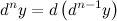
Получим формулы, выражающие дифференциалы высших порядков. Рассмотрим несколько случаев.
Случай независимой переменной
Первый дифференциал функции
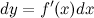
где - некоторое приращение независимой переменной , которое мы задаем сами и которое не зависит от . По определению
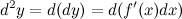
. То есть дифференциал второго порядка
Для вычисления дифференциала 
применим формулу дифференциала первого порядка к функции 
. Тогда получим:
Итак,
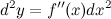
Рассматривая последовательно дифференциалы все более высокого порядка, получим формулу дифференциала -го порядка:
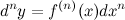
Пример
Задание. Найти дифференциал третьего порядка функции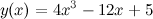 
Решение. По формуле
