Методом колебаний
Контрольные вопросы
1. Запишите уравнение собственных незатухающих колебаний. Дайте определения основных характеристик колебательного движения: амплитуды; фазы; периода; частоты; циклической частоты.
2. Запишите зависимость скорости колебательного движения от времени. Чему равно максимальное значение скорости?
3. Что называют моментом инерции тела относительно данной оси? Как рассчитать момент инерции материальной точки, твердого тела? В каких единицах измеряется момент инерции?
4. Сформулируйте теорему Штейнера. Сделайте поясняющий рисунок.
5. Запишите формулы для момента инерции шара и кубика относительно любой оси, параллельной оси, проходящей через центр масс этих тел.
6. Запишите формулу кинетической энергии тела, вращающегося относительно некоторой оси.
Тесты
1. Шар (1), два диска (2 и 3), тонкий стержень (4) и тонкостенный цилиндр (5) имеют одинаковую массу m. Какое из этих тел имеет момент инерции относительно оси ОО 1, равный I = mR 2?
Варианты ответа: а) 1; б) 2; в) 3; г) 4; д) 5; е) 1 – 3; ж) 1 – 4;
 |
з) все тела имеют момент инерции I = mR 2 ; и) среди ответов а - з нет верного.
2. Проволока AOB, согнутая под углом a (рис. 2.20), расположена в плоскости xOy. Как изменятся моменты инерции проволоки относительно осей Ox, Oy, Oz, если угол a увеличить?
| Варианты ответа | Относительно оси Ox | Относительно оси Oy | Относительно оси Oz |
| уменьшится | уменьшится | уменьшится | |
| увеличится | уменьшится | не изменится | |
| увеличится | увеличится | не изменится |
3. Сравнить моменты инерции однородного диска с вырезом (рис. 2.21) относительно осей Ox и Oy.
Варианты ответа: 1) IOx = I Oy; 2) IOx > I Oy; 3) IOx < I Oy.
4. Сравнить моменты инерции однородной пластины относительно осей I и II (рис. 2.22). Пластина и обе оси расположены в плоскости рисунка, при этом ось I проходит через центр масс пластины.
Варианты ответа: 1) I I = I II; 2) I I < I II; 3) I I > I II.
5. Какова полная кинетическая энергия цилиндра массой m при качении без скольжения со скоростью v по плоской поверхности?
Варианты ответа: 1)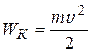 
; 2) 
; 3) 
;
4) 
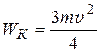; 5)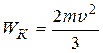 
.
6. 
Колебания махового колеса заданы уравнением j = 0,5 cos (2 t + p/3) рад. Чему равны амплитуда и период колебаний колеса?
Варианты ответа:
1) jm = 3рад, Т = 2 с; 2) jm = 0,5 рад, Т = 2 с;
3) jm = 0,5 рад, Т = p; 4) jm = 2 рад, Т = p/2;
5) jm = 0,5 рад, Т = p/3; 6) jm = 1 рад, Т = p;
7) jm = 1 рад, Т = -p; 8) jm = 1 рад, Т = p/3.
7. Маховое колесо совершает колебания. Какие из перечисленных величин достигают максимального значения в крайнем положении груза: угловая скорость w, угловое ускорение e, кинетическая энергия T, потенциальная энергия П?
Варианты ответа: 1) w, П; 2) w, Т; 3) e, П; 4) w, e, П.
8. Определить момент инерции однородного шара относительно неподвижной оси вращения О1О2, положение которой показано на рис. 2.23. Масса шара m, его радиус R.
Варианты ответа:
1) 
;
2) 
;
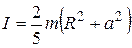3) 
;
4) 
.
9. На тело, вращающееся вокруг неподвижной оси, действует постоянный вращающий момент. Какая из перечисленных ниже величин изменяется со временем по линейному закону:
1) момент инерции тела;
2) угловое ускорение;
3) кинетическая энергия тела;
4) момент импульса тела относительно оси вращения;
5) угловая скорость;
6) ни одна из перечисленных величин не меняется по линейному закону.
10. 
Однородная пластинка со сторонами 2 а и 2 b массы m (рис. 2.24)имеет момент инерции IB относительно оси Z, проходящей через точку В перпендикулярно плоскости пластинки. Найти момент инерции пластинки IA относительно оси, проходящей через точку А и параллельной оси Z.
Варианты ответа: 1) IB + m (a2 + b2);
2) IB + m (a2 - b2); 3) IB + m (b2 – a2);
5) нет верного ответа.
11. Определить момент инерции однородного диска радиусом R и массой m относительно оси, перпендикулярной плоскости диска и проходящей через середину одного из радиусов.
Варианты ответа: 1) 
; 2) 
; 3) mR 2; 4)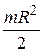 
.
Лабораторная работа 3-1
