Для простого модуля старший коефіцієнт взаємнопростий з ним. Визначимо множник k так, щоб. Матимемо. Домножаючи обидві частини заданої конгруенції на 10 за модулем 13, дістаємо 2 страница

Одержуємо:

Відповідь:

 

ІІ. Користуючись схемою Горнера:

а) розкласти многочлен f(x) за степенями (х – а) і одержаний розклад розташувати за спадними степенями х;

б) знайти канонічний розклад (відокремити кратні множники);

в) знайти значення многочлена f(x) та його похідних при х = а, якщо

f(x) = x ⁶ – 6 x ⁴ – 4 x ³ + 9 x ² + 12 x + 4, a = –2.

Розв‘язання.

а) За схемою Горнера маємо:

 

			–6	–4
–2		–2	–2			–6
–2		–4		–18		–72
–2		–6		–48
–2		–8		–116
–2		–10
–2		–12
–2

 

Звідси

f(x) = (x + 2)⁶ – 12(x + 2)⁵ + 54(x + 2)⁴ – 116(x + 2)³ +

+ 129(x + 2)² – 72(x + 2) + 16 = F (x + 2).

Розташуємо многочлен F (x + 2) за степенями х. запишемо х у вигляді
x = (x + 2) – 2 і за схемою Горнера розділимо F (x + 2) на двочлен (x + 2) – 2, одержуємо:

		–12		–116		–72
		–10		–48		–6
		–8		–12
		–6
		–4	–2	–4
		–2	–6

 

Отже, F (x + 2) = x ⁶ – 6 x ⁴ – 4 x ³ + 9 x ² + 12 x + 4.

б) Знайдемо d ₁ = (f, f¢), де f¢ = 6 x ⁵ – 24 x ³ – 12 x ² + 18 x + 12.

Застосовуючи алгоритм Евкліда для многочленів f і f¢, одержуємо:

d ₁ = x ⁴ + x ³ – 3 x ² – 5 x – 2,

d ₁¢ = 4 x ³ + 3 x ² – 6 x – 5.

Знаходимо d ₂ = (d ₁, d ₁¢); d ₂ = x ² + 2 x + 1;

d ₂¢ = 2 x + 2;

d ₃ = (d ₂, d ₂¢); d ₃ = x + 1;

d ₃¢ = 1;

d ₄ = (d ₃, d ₃¢); d ₄ = 1.

Отже, маємо:

Тому

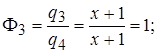
Враховуючи, що індекс F означає кратність, маємо: f(x) = (x – 2)² × (x + 1)⁴ – канонічний розклад многочлена f(x).

в) Для многочлена f(x) запишемо формулу Тейлора:

Порівняємо формулу з розкладом за степенями (х + 2). Одержуємо:

f (–2) = 16; f ¢(–2) = – 72; f ¢¢(–2) = 2!×129;

f ¢¢¢(–2) = –3!×116; f ^(IV) (–2) = 4!×54; f ^(V) (–2) = –5!×12; f ^(VI) (–2) = 6!.

 

ІІІ. Знайти раціональні корені многочлена

f(x) = 12 x ⁶ + 64 x ⁵ + 123 x ⁴ + 113 x ³ + 65 x ² + 24 x + 4.

Розв‘язання.

Старший коефіцієнт a ₀ = 12 ¹ 1. Тому многочлен, якщо має раціональні корені, то вони можуть бути як цілими, так і дробовими.

Шукаємо їх серед чисел:

Для скорочення обчислень знайдемо межі коренів многочлена f(x). Так як коефіцієнти многочлена f(x) додатні, то він не має додатних коренів і тому верхня межа дорівнює нулеві.

Знайдемо нижню межу многочлена f(x) методом Ньютона.

f(x) = 12 x ⁶ + 64 x ⁵ + 123 x ⁴ + 113 x ³ + 65 x ² + 24 x + 4.

Для f(–x) знаходимо методом Ньютона верхню межу: ВМ = –3, отже,
НМ = – 3 – нижня межа для многочлена f(x).

Отже, усі корені многочлена f(x) знаходяться на проміжку (–3; 0). Тому залишилися для випробувань числа:

 

Знаходимо цілі корені, ними можуть бути числа –1, –2. обчислюємо
f (1) = 405, f (–1) = 3. так як f (–1) ¹ 0, то число –1 не є коренем f(x). Для числа –2 застосовуємо “сито”. Результат запишемо у таблицю:

 

a
–2	ц	ц

 

Отже, число –2 підозріле на корінь.

За схемою Горнера перевіряємо, чи буде –2 коренем многочлена та визначимо його кратність:

–2
–2
–2				–1

 

З таблиці видно, що a = –2 є двократним коренем многочлена f(x). Знаходимо дробові корені. До чисел, що залишилися для перевірки, застосовуємо “сито”. Результати заносимо до таблиці:

 

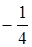
	ц	д	ц	д	ц	д	д
	ц		д		ц

 

Числа і 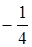підозрілі на корінь. Так як –2 є двократним коренем многочлена f(x) = (x + 2 ) ² g(x), де g(x) = 12 x ⁴ + 16 x ³ + 11 x ² + 5 x + 1, то кожне з чисел і 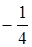перевіряємо на корінь за схемою Горнера для многочлена g(x):

 

		–2

 

Звідси маємо: a = є двократним коренем многочлена g(x) і тому

f(x) = (x + 2 ) ² × (x + 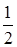)² × j(x),

де j(x) = 12 x ² + 4 x + 4.

Перевіряємо число a = 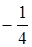на корінь для многочлена j(x).

 

 

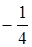
Отже, a = 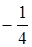не є коренем. Тому многочлен f(x) має два двократні корені a₁ = –2, a₂ = .

ІV. Виразити через елементарні симетричні многочлени многочлен.

f (x ₁, x ₂, x ₃) = x ₁³ x ₂ + x ₁³ x ₃ + x ₁ x ₂³ + x ₁ x ₃³ + x ₂³ x ₃ + x ₂ x ₃³.

Розв‘язання.

Складемо розрахункову таблицю:

 

Система показників вищого члена	Вищий член	Відповідна комбінація елементарних симетричних многочленів
3 1 0	x 13 x 2 x 30	s12s2
2 2 0	bx 12 x 22 x 30	b s22
2 1 1	cx 12 x 2 x 3	c s1s3

 

Тоді f (x ₁, x ₂, x ₃) = s₁²s₂ + b s₂² + c s₁s₃, (*)

де s₁ = x ₁ + x ₂ + x ₃, s₂ = x ₁ x ₂ + x ₁ x ₃ + x ₂ x ₃, s₃ = x ₁ x ₂ x ₃.

Поклавши x ₁ = 1; x ₂ = –1; x ₃ = 0, одержуємо: s₁ = 0, s₂ = –1, s₃= 0, f = –2.

Підставляючи знайдені значення у вираз (*), одержуємо:

–2 = b × (–1)²; b = –2,

тобто f (x ₁, x ₂, x ₃) = s₁²s₂ –2s₂² + c s₁s_3. (**)

Надаємо значень x ₁ = x ₂ = 1, x ₃ = –1, одержуємо:

s₁ = 1, s₂ = –1, s₃ = –1, f = –2.

Підставляємо знайдені значення у вираз (**), одержуємо: c = –1. Отже,

f (x ₁, x ₂, x ₃) = s₁²s₂ –2s₂² – s₁s_3.

 

V. У множині дійсних чисел розв’язати систему рівнянь:

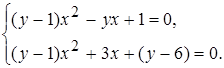
Розв‘язання.

Складаємо результант і знаходимо всі його корені. Маємо:

 

 

Многочлен y ³ – 9 y ² + 24 y – 20 має раціональний корінь у = 2. Отже,
R(y) = 2(y – 1)(y – 2)²(y – 5).

b₁ = 1; b_{2, 3} = 2; b₄ = 5.

Розглянемо випадок 1) b₁ = 1. Одержуємо:

Спільного кореня ці многочлени не мають.

2) Нехай b_{2, 3} = 2. Тоді

Спільний корінь a₂ = 1 і тому a₂ = 1, b₂ = 2 є розв‘язком даної системи.

3) Нехай b₄ = 5. Маємо:

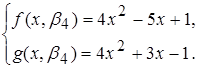
Спільний корінь тут . Отже, , b₄ = 5 – другий розв‘язок системи рівнянь.

Відповідь: (1, 2); (, 5).

 

VI. Позбавитися від алгебраїчної ірраціональності в знаменнику дробу

.

Розв‘язання.

Заданий дріб є значенням раціонального дробу при , яке є коренем незвідного у полі Q многочлена h(x) = x ³ – 7. Многочлени g(x) і f(x) взаємно прості. Знайдемо лінійне зображення їхнього найбільшого спільного дільника.

Ділення многочленів виконаємо “кутом”:

_ x 3 – 7	x 2 – x + 3
x 3 – x 2 + 3 x	x + 1
	_ x 2 – 3 x – 7
	x 2 – x + 3
	– 2 x – 10

x ³ – 7 = (x ² – x + 3)(x + 1) – 2 x – 10,

h(x) = g(x) (x + 1) – (2 x + 10).

2 x + 10 = – h(x) + g(x) (x + 1);

_ x 2 – x + 3	– 2 x – 10
x 2 + 5 x
	_ – 6 x + 3
	– 6 x – 30

x ² – x + 3 = (– 2 x – 10)() + 33,

g(x) = – (2 x + 10)() + 33.

Звідси

33 = g(x) + (2 x + 10)() = g(x) + (– h(x) + g(x) (x + 1))() =

= g(x) (1 + (x + 1)()) + h(x) () =

= g(x) (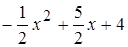) + h(x) ().

Оскільки , то

 

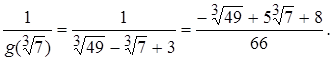
VІІ. Довести, що число a є алгебраїчним і знайти його мінімальний многочлен, якщо .

Розв‘язання.

Число a називають алгебраїчним відносно поля Р, якщо воно є коренем деякого многочлена над полем Р. Отже, нам треба знайти незвідний над полем Р многочлен, коренем якого є число . Для цього розглянемо рівняння . Число a є коренем цього рівняння. Обидві частини цього рівняння підносимо до другого степеня .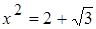

Позбавляємося від ірраціональних коефіцієнтів:

,

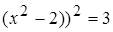звідси одержуємо рівняння з раціональними коефіцієнтами x ⁴ – 4 x ² + 1 = 0.

В результаті зроблених перетворень не відбулося втрати коренів. Отже, число є коренем одержаного рівняння або многочлена
f(x) = x ⁴ – 4 x ² + 1. Цей многочлен над полем раціональних чисел незвідний. Так як степінь многочлена f(x) дорівнює 4, то число є алгебраїчним числом 4-ого степеня, а його мінімальним многочленом є многочлен
f(x) = x ⁴ – 4 x ² + 1.

 

VІІІ. Розкласти на незвідні у полі Q множники многочлен

f(x) = x ⁴ + 2 x ³ – 3 x ² – 5 x + 2.

Розв‘язання.

Нехай многочлен f(x) є звідним у полі Q, тобто його можна розкласти в добуток не менше як двох многочленів ненульового степеня з кільця Q [ x ]. Щоб розкласти многочлен f(x) на множники, застосуємо метод невизначених коефіцієнтів. При цьому досить розглянути два випадки можливого розкладу:

1) обидва множники мають степінь 2;

2) один множник має степінь 1, а другий 3.

Нехай f(x) = (ax ² + bx + c)(dx ² + mx + n). (1)

Тоді з рівності

x ⁴ + 2 x ³ – 3 x ² – 5 x + 2 = adx ⁴ + (am + bd) x ³ + (an + bm + cd) x ² + (bn + cn) x + cn

маємо

(2)

Розв‘яжемо цю систему рівнянь в цілих числах. Знаходимо a = d = 1 або
a = d = –1, з останнього рівняння – c = 1, n = 2, c = 2, n = 1, c = –2, n = –1, c = –1, n = –2. Розглянемо кожен з восьми можливих варіантів.

1) Якщо a = d = 1, c = 1, n = 2, то маємо систему:

.

Ця система несумісна.

2) У кожному з решти варіантів несумісними є також системи рівнянь:

Це означає, що система рівнянь (2) несумісна і многочлен f(x) не розкладається в добуток двох многочленів другого степеня з цілими коефіцієнтами.

Припустимо, що розклад (1) виконується при дробових числах a, b, c, d, m, n. Зведемо до найменшого спільного знаменника коефіцієнти многочленів g ₁ (x) = ax ² + bx + c, g ₁ (x) = dx ² + mx + n та винесемо за дужки ці знаменники і найбільші спільні дільники чисельників обох многочленів. Одержуємо розклад

,

де (r, s) = (a ₁, b ₁, c ₁) = (d ₁, m ₁, n ₁) = 1.

Оскільки коефіцієнти многочлена f(x) є цілими числами, то всі коефіцієнти многочлена 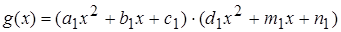мають ділитися на число s, а тому й на кожен його простий дільник р.

Разом з тим, серед кожної трійки чисел a ₁, b ₁, c ₁ та d ₁, m ₁, n ₁ знайдуться числа, які не діляться на р. тому серед коефіцієнтів a ₁ d ₁, a ₁ m ₁ + b ₁ d ₁,
a ₁ n ₁ + b ₁ m ₁ + c ₁ d ₁, b ₁ n ₁ + c ₁ m ₁ і c ₁ n ₁ многочлена g(x) знайдеться такий, що не ділиться на р. тому s = 1 і ми дістанемо розклад (1) з цілими коефіцієнтами, що неможливо.

Нехай f(x) =(ax + b)(cx ³ + dx ² + mx + n). Тоді з рівності

x ⁴ + 2 x ³ – 3 x ² – 5 x + 2 = acx ⁴ + (ad + bc) x ³ + (am + bd) x ² + (an + bm) x + bn

маємо:

Одним з розв‘язків цієї системи є a = c = n = 1, b = 2, d = 0, m = –3. Отже, f(x) = (x + 2)(x ³ – 3 x + 1), тобто многочлен f(x) звідний у полі Q.

Додаток: таблиці первісних коренів та індексів

 

Просте число 3 Первісні корені: 2

N

I

Просте число 5 Первісні корені: 2, 3

N

I

Просте число 7 Первісні корені: 3, 5

N

I

Просте число 11 Первісні корені: 2, 6, 7, 8

N

I

Просте число 13 Первісні корені: 2, 6, 7, 11

N

I

Просте число 17 Первісні корені: 3, 5, 6, 7, 11, 12, 14

N

I

Просте число 19 Первісні корені: 2, 3, 10, 14, 15

N

/

б

Просте число 23 Первісні корені: 5, 7, 10 11, 14, 15, 17, 19, 20, 21

N

/

Просте число 29 Первісні корені: 2, 3, 8, 10, 11, 14, 15, 18, 19, 21, 26, 27

N

/

Просте число 31 Первісні корені: 3, 11, 12, 13, 17, 21, 22, 24

N

/

4'

Просте число 37 Первісні корені: 2, 5, 13, 15, 17, 18, 19, 20, 22, 24, 32, 35

N

/

Просте число 41 Первісні корені: 6, 7, 11, 12, 13, 15, 17, 19, 22, 24, 26, 28, 29, 30, 34, 35

N

/

б

§

Просте число 43 Первісні корені: 3, 5, 12, 18, 19, 20, 26, 28, 29, 30, 33, 34

N

I

б

Просте число 47 Первісні корені: 5, 10, 11, 13, 15, 19, 20, 22, 23, 26, 29, 30, 31, 33,

N

/

Просте число 53 Первісні корені: 2, 3, 5, 8, 12, 14, 18, 19, 20, 21, 22, 26, 27, 31, 32,

N

/

Просте число 59 Первісні корені: 2, 6, 8, 10, 11, 13, 14, 18, 23, 24, 30, 31, 32, 33. 34,

N

/

.35