МН {  } күштер жүйесінің әсерінен инерциалдық Оxyz санақ жүйесіне қатысты қозғалатын болсын, және күштер арасына байланыстардың реакциялары да кіреді деп есептейміз.
} күштер жүйесінің әсерінен инерциалдық Оxyz санақ жүйесіне қатысты қозғалатын болсын, және күштер арасына байланыстардың реакциялары да кіреді деп есептейміз.
(6.2) теңдеуін декарт координат өстеріне проекциялап, декарт координаттарындағы қозғалысының дифференциалдық теңдеулерін (ҚДТ) аламыз
 (6.3)
(6.3)
табиғи өстерге проекциялап, нүкте қозғалысының табиғи дифференциалдық теңдеулерін аламыз
 ; (6.4)
; (6.4)
ҚДТ нүкте динамикасының екі негізгі есебін шешу үшін қолданылады:
1-негізгі есеп: нүкте қозғалысы бойынша оған түсетін күшті анықтау. Мұнда МН қозғалысының теңдеулерін дифференциалдап, нәтижелерін (6.3) немесе (6.4) теңдеулеріне қою керек, содан нүктеге түсетін күш анықталады;
2-негізгі есеп: нүктеге түсетін күштер бойынша оның қозғалысын анықтау. Мұнда жалпы жағдайда (6.3) немесе (6.4) дифференциалдық теңдеулерінің екінші интегралдарын табу керек. Дербес жағдайларда ҚДТ айнамалыларды бөлу әдісінің көмегімен интегралдалуы мүмкін.
Материялық нүктенің салыстырмалы қозғалысы
Динамика заңдары тек қана инерциалдық СЖ-нде орындалады. Материялық нүктенің кейбір СЖ-не қатысты қозғалысын қарастырайық және осы СЖ инерциалдық СЖ-не қатысты еркінше қозғалатын болсын. P нүктесі {  } күштер әсерінен қозғалатын болсын. Инерциалдық СЖ-нде динамиканың негізгі (6.2) теңдеуі орындалады. Нүктенің абсолют үдеуі (5.17) формуласымен табылады
} күштер әсерінен қозғалатын болсын. Инерциалдық СЖ-нде динамиканың негізгі (6.2) теңдеуі орындалады. Нүктенің абсолют үдеуі (5.17) формуласымен табылады
 (6.5)
(6.5)
(6.5) теңдігін (6.4) теңдігіне қойып, түрлендіреміз
 (6.6)
(6.6)
Келесі белгілерді қабылдаймыз
 (6.7)
(6.7)
және  (6.8)
(6.8)
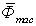 және
және  векторлары сәйкес тасымал және кориолис инерция күштері деп аталады.
векторлары сәйкес тасымал және кориолис инерция күштері деп аталады.
(6.6) теңдігін келесі түрде жазуға болады
 (6.9)
(6.9)
(6.9) теңдеуі МН-нің салыстырмалы қозғалысы динамикасының негізгі теңдеуі деп аталады. МН-нің салыстырмалы қозғалысының теңдеулері абсолют қозғалысының теңдеулері секілді, түсетін күштерге тасымал және кориолис инерция күштерін қосып, құрастырылады. Қозғалатын инерциалдық емес СЖ-нің бақылаушы тасымал және кориолис инерция күштерін шынайы әсер ететін күштер секілді қабылдайды. Бірақ ол дұрыс емес, өйткені инерциалдық емес СЖ үшін механиканың Ньютон заңдары орындалмайды, сондықтан құбылыстарды алдыңғы аксиомалар қолдануымен қарастыруға болмайды.
МН-нің салыстырмалы қозғалысы негізгі теңдеуінің дербес жағдайлары:
а) ілгерілемелі тасымал қозғалыс кезінде

 (6.10)
(6.10)
б) түзу сызықты бірқалыпты тасымал қозғалыс кезінде
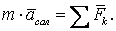 (6.11)
(6.11)
Мұнда (6.11) мен (6.2) бірдей болады, өйткені  . Сондықтан, бұл санақ жүйесі инерциалдық болады. Механикалық тәжірибелер арқылы санақ жүйесі тыныштықта екенін немесе ілгерілемелі бірқалыпты және түзу сызықты қозғалыста екенін анықтау мүмкін емес (Галилейдің салыстырмалылық принципі);
. Сондықтан, бұл санақ жүйесі инерциалдық болады. Механикалық тәжірибелер арқылы санақ жүйесі тыныштықта екенін немесе ілгерілемелі бірқалыпты және түзу сызықты қозғалыста екенін анықтау мүмкін емес (Галилейдің салыстырмалылық принципі);
в) салыстырмалы тыныштық қалпында
 (6.12)
(6.12)
Бұл МН-нің салыстырмалы тепе-теңдігінің теңдеуі.






