Қатты денеге түсетін күшті оның денеге әсерін өзгертпей, дененің кез келген басқа нүктесіне, күштер жұбын қосып, өзіне параллель көшіруге болады (2.4 сурет); жұптың моменті күштің сол нүктеге қатысты моментіне тең болуы тиіс.
2.5 Күштер жүйесін берілген центрге келтіру
АҚД-ге әсер ететін кез келген күштер жүйесін бір центрге келтіруге болады, сонда барлық күштер келтіру центріне түсетін жүйенің бас векторына тең бір күш пен моменті жүйенің сол центрге қатысты бас моментіне тең бір жұпқа ауыстырылады (2.5 сурет)
(2.11)
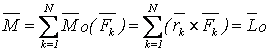. (2.12)
Мұнда 
келтіру центрінің таңдалуына тәуелсіз, ал 
– тәуелді.
АҚД-ге әсер ететін екі күштер жүйесі, олардың бас векторлары бірдей және кез келген нүктеге қатысты бас моменттері бірдей болғанда баламалы.
Вариньон теоремасы: егер күштер жүйесінің тең әсерлі күші болса, оның кез келген нүктеге немесе өске қатысты моменті жүйенің барлық күштерінің сол нүктеге немесе өске қатысты моменттерінің қосындысына тең.
Дәріс. Күштер жүйелерінің тепе-теңдік шарттары. Үйкеліс. Ауырлық центрі.
Дәрістің мазмұны: күштер жүйелерінің тепе-теңдік шарттары, сырғанау үйкелісі мен домалау үйкелісі, қатты денелердің ауырлық центрлері.
Дәрістің мақсаты: кеңістік және жазық күштер жүйелерінің тепе-теңдік шарттарын анықтау, үйкеліс болғанда есептерді шешудің ерешеліктерін қарастыру, денелердің ауырлық центрлерін анықтауды үйрену.
Күштер жүйесінің тепе-теңдік шарттары
Денеге әсер ететін кез келген күштер жүйесі оның бас векторына тең бір күшке және моменті жүйенің кез келген О центріне қатысты бас моментіне тең күштер жұбына баламалы. Олай болса күштер жүйесі тепе-теңдікте болу үшін және нөлге тең болуы қажетті де жеткілікті. Сондықтан тепе-теңдіктің шарттары векторлық түрде осылай жазылады
, (3.1)
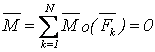. (3.2)
Бұл шарттар келесі тепе-теңдіктің аналитикалық шарттарына баламалы
, 
, 
,
, 
, 
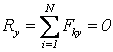, (3.3)
яғни АҚД-ге әсер ететін кез келген күштер жүйесінің тепе-теңдігі үшін барлық күштердің декарт координат жүйесінің үш өсіне проекцияларының қосындылары және сол өстерге қатысты барлық күштердің моменттерінің қосындылары нөлге тең болуы қажетті де жеткілікті.
Кеңістік параллель күштер жүйесі үшін (Oz өсі күштерге бағыттас) келесідей жазылады
, , . (3.4)
Кез келген жазық күштер жүйесінің тепе-теңдік шарттарының бірінші түрі: күштердің екі координат өсіне проекцияларының қосындылары және кез келген центрге қатысты күштердің алгебралық моменттерінің қосындысы нөлге тең болуы қажетті де жеткілікті
, , 
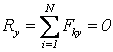. (3.5)
Екінші түрі
, 
, 
, (3.6)
мұнда 
түзуі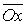 
өсіне перпендикуляр емес болу керек.
Үшінші түрі
, , (3.7)
мұнда А, В, С бір түзудің бойында жатпау керек.
Жазық параллель күштер жүйесі үшін тепе-теңдік шарттары келесідей
, (3.8)
(мұнда Ox өсі күштерге перпендикуляр болмау керек) немесе
, 
, (3.9)
мұнда А мен В нүктелерінен өтетін түзу күштерге параллель болмау керек.
