, (2.4.15) при разбиении времени t на малые отрезки D t, а также использовать дискретизацию времени t = k D t по целочисленным отсчетам k = 0, 1, 2, …, то уравнение (2.4.4) можно записать в рекурсивной форме
x (k +1) @ (I + D t A) x (k) + D t B u (k). (2.4.16)
Точность решения уравнения (2.4.16) повышается с уменьшением D t.
Метод дискретизации уравнения состояния оказывается чрезвычайно полезным при вычислении временных характеристик нелинейных систем. В этом случае уравнение состояния имеет общий вид
, (2.4.17)
где f есть функция вектора состояния x и вектора входа u.
Используя (2.4.15) легко получить
x (k +1) = x (k) + D t f [ x (k), u (k), k ]. (2.4.18)
2.5. Идентификация и устойчивость дискретных моделей
линейных систем.
Предположим, что наблюдается некоторый дискретный сигнал yn. Рассмотрим его дискретную модель
yn = a10 yn-1 + a20 yn-2 + a30 yn-3 + 
+ hn,
n = 0, 1, 2, …, N –1. (2.5.1)
В данной модели предполагается, что входной сигнал системы
xn , z =
имеет некоторую задержку z и описывается набором L импульсов dn с неизвестными амплитудами D xn, также подлежащими идентификации.
Будем считать, что помеха hn имеет нормальный гауссовый характер и некоррелирована (см. Модуль 1).
Будем искать параметры a10, a20, a30 и D xn дискретно-разностной динамической модели (2.51) методом наименьших квадратов, минимизируя энергию помехи
СКО = 
= 
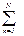[ yn – a1 yn-1 – a2 yn-2 – a3 yn-3 –
– 
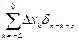]2Þ min. (2.5.2)
Тогда, из условия ¶ОШ/¶ aij = ¶ОШ/¶D xk = 0, получим следующую систему 3-х линейных уравнений для оценивания параметров динамической модели
Z 11 a 1 + Z 12 a 2 + Z 13 a 3= R 1, (2.5.3)
Z 21 a 1 + Z 22 a 2+ Z 23 a 3= R 2,
Z 31 a 1 + Z 32 a 2 + Z 33 a 3 = R 3, где
Z 11 = 
– 
= (2.5.4)
= (y0 y0 + y1 y1 +…+ yN-1 yN-1) – (yz-1 yz-1 + yz-2 yz-2 +…+ yz-L-1 yz-L-1),
Z12 = 
– 
=
= (y1 y0 + y2 y1 +…+ yN-1 yN-2)– (yz-1 yz-2 + yz-2 yz-3 +…+ yz-L-1 yz-L-2),
Z13 = 
– 
=
= (y2 y0 + y3 y1 +…+ yN-1 yN-3)– (yz-1 yz-3 + yz-2 yz-4 +…+ yz-L-1 yz-L-3),
Z21 = 
– 
= Z12,
Z22 = 
– 
=
= (y0 y0 + y1 y1 +…+ yN-2 yN-2) ‑ (yz-2 yz-2 + yz-3 yz-3 +…+ yz-L-2 yz-L-2),
Z23 = 
– 
=
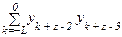= (y1 y0 + y2 y1 +…+ yN-2 yN-3) – (yz-2 yz-3 + yz-3 yz-4 +…+ yz-L-2 yz-L-3),
Z31 = 
– 
= Z13,
Z32 =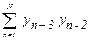 
– 
= Z23,
Z33 = 
– 
=
= (y0 y0 + y1 y1 +…+ yN-3 yN-3) – (yz-3 yz-32 + yz-4 yz-4 +…+ yz-L-3 yz-L-3).
Правые части системы уравнений (2.5.4) определяются как
R1 = 
– 
= (2.5.5)
= (y1 y0 + y2 y1 +…+ yN yN-1)–(yz yz-1 + yz-1 yz-2 + yz-2 yz-3 +…+ yz-L yz-L-1),
R2 = 
– 
=
= (y2 y0 + y3 y1 +…+ yN yN-2) –(yz yz-2 + yz-1 yz-3 + yz-2 yz-4 +…+ yz-L yz-L-2),
R3 = 
– 
=
= (y3 y0 + y4 y1 +…+ yN yN-3)–(yz yz-3 + yz-1 yz-4 + yz-2 yz-5 +…+ yz-L yz-L-3).
Из (2.5.3) следует, что Z21 = Z12, Z31 = Z13, Z32 = Z23. Поэтому детерминант системы и ее алгебраические дополнения соответственно равны
Detz = Z11 Z22 Z33 ‑ Z11 Z232 ‑ Z22 Z132 ‑ Z33 Z122 + 2 Z12 Z13 Z23 ,
Deta1 = R1 (Z22 Z33 ‑ Z232) + (2.5.6)
+ R2 (Z13 Z23 ‑ Z12 Z33) + R3 (Z12 Z23 ‑ Z13 Z22),
Deta2 = R1 (Z13 Z23 ‑ Z12 Z33) +
+ R2 (Z11 Z33 ‑ Z132) + R3 (Z12 Z13 ‑ Z11 Z23),
Deta3 = R1 (Z12 Z33 ‑ Z13 Z22) +
+ R2 (Z12 Z13 ‑ Z11 Z23) + R3 (Z11 Z22 ‑ Z122).
Параметры модели оцениваются как
a1 = Deta1 / Detz = (2.5.7)
= 
;
a2 = Deta2 / Detz =
= 
;
a3 = Deta3 / Detz =
= 
.
Коэффициенты D xn, вычисляются по оцененным параметрам модели как
D xn = yn – a10 yn-1 – a20 yn-2 – a30 yn-3, (2.5.8)
n = 0, 1, 2, …, N -1.
Спрашивается – как произвести оценку устойчивости полученной модели (2.5.1).
Возможно два подхода.
Теоретическая устойчивость дискретно-разностной модели (2.5.1) проверяется на основании известных в теории автоматического регулирования условий Рауса-Гурвица
a10 + a20 + a30 < 1,
a10 – a20 + a30 > –1, (2.5.9)
a302 + 3a102 + 3a20 (a30 – a10) – 4a30 a10 +
+ 9a30 + 8a20 – 9a10 > – 8
или более «мягких» условий
a10 + a20 + a30 < 1, (2.5.10)
a10 – a20 + a30 > –1,
3(a30 + 1) + a20 > a1,
3(a30 –1) < a10 + a20.
Практическая устойчивость дискретно-разностной модели (2.5.1) проверяется по условию
ОШмод / Энергия сигнала = 
[ yn – zn ] 2 / yn 2 < D , (2.5.11)
где D – некоторый порог устойчивости (D £ 1); а zn – модель, построенная в соответствии с (2.5.1) для оцененных параметров.
2.6. Экспертные корреляционно-экстремальные
системы управления для спектральной
компьютерной квалиметрии.
Корреляционное сравнение данных.
При контроле качества технологических процессовили самих изделий необходимо проводить сравнение наблюдаемых сигналов (данных) X = [ X 1, X 2, …, XN ] c некоторой конечной совокупностью { S m } = {[ X 1 m, X 2 m, …, XNm ]} опорных сигналов (m = = 1, 2, …, M). На основании результатов сравнения вырабатывается управляющее воздействие u (X, { S m }). В таких системах основная тяжесть задачи падает на синтез методов, алгоритмов и систем сравнения наблюдаемых и эталонных сигналов.
Для примера, на рис. 2.6.1 приведена система контроля качества жидких сред по оптическому светорассеянию. Луч лазера Л освещает кювету Кс исследуемой жидкостью. Рассеянный свет попадает на детектор Д, формирующий спектр X рассеяния (угловой, цветовой, частотный, оптический, инфракрасный, комбинационный – в зависимости от конкретной задачи и исследуемой жидкости). Данный спектр поступает в устройство сравнения УС (аналоговое, цифровое, цифроаналоговое), куда поступают эталонные спектры S m, хранящиеся в базе данных БД. Само УС и БД могут быть выполнены как на основе цифровой техники, так и аналоговой голографической техники, проводить сравнение последовательно или параллельно. УС вырабатывает сигналы сравнения mm = m (X,{ S m }), на основе которых блок управления БУ формирует управление u ({ mm }).
|
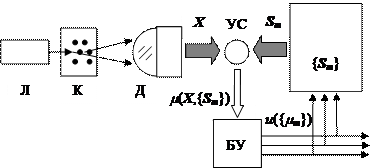
Рис. 2.6.1
Как видно из рисунка, управление, вырабатываемое в контуре обратной связи, осуществляет специализированный поиск в БД. Например, в простейшем случае ищется максимальное значение mm.
Предположим, что наблюдаемые спектральные данные X описываются аддитивной моделью в виде
X = S + H, (2.6.1)
где S – вектор-столбец опорного сигнала, а H – вектор-столбец аддитивных нормально распределенных нестационарных помех с некоррелированными компонентами, имеющими нулевые математические ожидания á H ñ = 0 и дисперсии sn2 = á Hn2 ñ.
Оказывается, в зависимости от конкретного вида модели (2.6.1) возможны различные методы оптимального сравнения неизвестных и опорных данных. При этом, оптимальность понимается в смысле экстремума критерия различительной способности при сравнении.
Рассмотрим следующие случаи применения оптимальных корреляторов – алгоритмов, реализующих сравнение данных.
Амплитуда сигнала и мощности помех á H2n ñ известны.
Тогда УС формирует корреляционную меру сходства
m (X, S ú F) = S T F T FX = å Nn (F) n 2(S) n (Х) n, (2.6.2) (7)
(F) n = 1/ sn = 1 / á H2n ñ1/2. (8)
Амплитуда сигнала известна, а мощности помех á H2n ñ
неизвестны.
Тогда УС формирует корреляционную меру сходства
m (X, S ú F) = S T F T FX / [(X – S) T F T F (X – S) + 1], (2.6.3)
(F) n = 1/ sn *, где sn *2 – оценки мощности помех.
Амплитуда сигнала и мощности помех неизвестны.
Тогда УС формирует корреляционную меру сходства
m (X, S ú F) = 1/ [1 – (S T F T FX)2 /(S T F T FS) (X T F T FX)], (2.6.4) (10)
(F) n = 1 / sn *, где sn *2 – оценки мощности помех.
Методы спектральной компьютерной квалиметрии.
Практически все стандарты по сертификации качества продукции различных отраслей пищевых производств включают мероприятия по оценке органолептических свойств (признаков или характеристик) пищевых сред – сырья и готовых продуктов, которые гораздо больше, чем физико-химические свойства и пищевая ценность, влияют на выбор потребителей и, в конечном счете, формируют их спрос. Органолептическими свойствами пищевых продуктов являются внешний вид, текстура, вкус и запах, аромат. К сожалению, осуществить грамотную оценку органолептических свойств пищевых продуктов, тем более оперативную и в условиях массового производства, могут далеко не все, даже подготовленные эксперты. Необходимы некоторые «эталонные» качества, основанные на опыте и природных способностях. В то же время, создать подобное количество датчиков различных органолептических свойств, какое имеется у органов осязания и обоняния человека практически невозможно. В этих условиях и была предложена информационная технология спектральной компьютерной квалиметрии (СКК).
Идея СКК основана на разработке специальных или же использовании уже известных инструментальных средств (методов, датчиков и приборов) оперативного контроля разнообразных физико-химических, оптических, реологических и биологических характеристик пищевых сред совместно с автоматизированными (компьютерными) экспертными системами для связывания «спектров» (совокупностей) получаемых инструментальных характеристик с соответствующими органолептическими признаками и другими (потребительскими) характеристиками, оцениваемыми или инструментально измеряемыми опытными экспертами. В дальнейшем, с накоплением данных и знаний, такие экспертные системы должны самостоятельно давать оперативные оценки органолептических и потребительских свойств исследуемых пищевых сред, как отклик на входные запросы в виде соответствующих инструментальных характеристик данных сред. Реализация же СКК требует привлечения современных «синтетических» знаний, а также разработки специальных методов и средств.
Идея СКК наглядно показана на рисунке 2.6.1.
 |
Рис. 2.6.1
СКК особенно эффективна в области управления качеством продукции, основанной на органических средах (растительные и минеральные масла, нефтепродукты), а также вин и ликероводочной продукции, что связано, в первую очередь, с возможностью практического осуществления оперативного спектрального анализа данных жидких сред в широком диапазоне электромагнитных волн.
Для оперативного контроля разнообразных сред представляют интерес следующие методы получения спектральных данных.
1. Метод теплового удара – мгновенное изменение локальной (поверхностной) температуры среды (например, излучением полупроводникового лазера) и измерение температурного отклика среды.
2. Метод акустического удара – мгновенное возбуждение в среде акустических (ультразвуковых) шумов и измерение их спектральных характеристик.
3. Метод электровозбуждения – возбуждение электротока в среде и измерение спектра мощности его флуктуаций.
4. Метод инфракрасной и СВЧ (субмиллиметровой, миллиметровой и сантиметровой) спектроскопии – измерение спектральных свойств среды в диапазонах длин волн от (0,75¸80) мкм до (0,30¸30,00) смсоответственно.
5. Метод оптической спектроскопии – измерение спектральных свойств среды в диапазонах длин волн от (0,20¸ 1000) мкм.
6. Методы жидкостной и газовой хроматографии – разделение вещества на фракции в соответствие их молекулярного состава.
В любом из перечисленных методов формируют спектр S (w) отклика исследуемых сред на внешнее воздействие (см. стр. 44 – 45). Данные спектры несут косвенную информацию о микро- и макроскопических, физико-химических и структурных свойствах сред. При этом количество M = W / D W потенциальных свойств определяется максимальной шириной W полосы отклика (0 £ w £ W) и разрешающей способностью D W метода.
В результате исследуемая среда с различными потребительскими свойствами 1 и 2 потенциально может откликаться близкими спектральными распределениями S 1(w) и S 2(w), носящими нечетко выраженные различия, как показано на рис. 2. 6.3. Приведенные спектральные распределения измерены с 10% точностью (± H). Поэтому необходимы специальные высокоразрешающие методы численной обработки для их различения.
Рис. 2.6.3
К сожалению, даже не сплошные, а линейчатые спектры пищевых сред носят нечеткий характер, что обусловлено их многокомпонентным составом. Так, на рис. 2.6.4 приведен спектр аминокислотного состава растительного масла, полученный хроматографическим методом, при котором последовательно во времени, путем диффузии, выделяются аминокислотные фракции в соответствии с их молекулярной массой – аминокислоты с легкими молекулярными массами выделяются первыми.
Из рисунка видно, что хроматографические спектры при наличии всех аминокислот могут различаются только своими огибающими.
 |
Причина нечеткости спектральных данных пищевых сред заключается в том, что относительно узкие резонансные линии их многочисленных компонентов накладываются друг на друга, что приводит к «смазыванию» спектральных распределений.
Рис. 2.6.4
Это легко пояснить, опираясь на теорию спектрального анализа, опирающегося на рассмотренную выше теорию частотных характеристик систем (см. стр. 44 – 45). Спектральное распределение функции отклика среды для «частиц» (атома, молекулы, молекулярных соединений) одного «к»-го сорта, соответствующее зависимости мощности поглощения от частоты w возбуждения, вблизи резонанса wк, описывается функцией Лоренца
Sк (w) @ S0 wк Dwк /[(wк – w)2 + Dwк 2], (2.6.5)
где Dwк – ширина поглощения частицы «к»-го сорта.
Отсюда следует, что спектральное распределение функции отклика среды, содержащей различные частицы (к = 1, 2, …, К) имеет вид
Så (w) = åк Sк (w) @ åк S0 wк Dwк / [(wк – w)2 + Dwк 2]. (2.6.6)
Простые вещества (газы, жидкости), состоящие из небольшого количества разнотипных невзаимодействующих «частиц», имеют лорентцевские спектры показанные на рисунке 2.6.5.
 |
Рис. 2.6.5
Пищевые среды, как и другие многокомпонентные вещества, находящиеся в конденсированном состоянии, состоят из огромного количества различных «частиц», лорентцевские спектры которых значительно уширены из-за связей, удерживающих данные частицы в едином комплексе.
В качестве наглядного примера на рис. 2.6.6. приведен спектр поглощения среды состоящей из частиц трех разных типов.
Видно, что из-за наложения лорентцевских спектральных линий и большой ширины каждой из них результирующий спектр приобретает «смазанный» или нечеткий характер. Вполне естественно, что спектральное разрешение уменьшается с уменьшением полосы частот используемых воздействий. С падением разрешения падает и способность различения близких спектральных распределений, особенно в нерезонансной области спектра поглощения.
 |
Рис. 2.6.6
Основная проблема спектральной компьютерной квалиметрии – уверенное различение «близких» спектральных распределений. Для решения этой проблемы возможно использовать рассмотренные выше корреляторы.
Другой проблемой является формирование базы данных «опорных» спектров { S m = [ S 1 m, S 2 m, …, SNm ]} (m = 1, 2, …, M) и «эталонных» векторов { Y m = [ Y 1 m, Y 2 m, …, YNm ]} описания свойств пищевых продуктов, а также – построение экспертных правил (знаний), на основании которых будет синтезироваться вектор отклика Y на неизвестный входной спектр X.
Построение экспертных правил возможно осуществить на основе моделей регрессионных зависимостей, минимизирующих СКО соответствующих выходов модели
Y k (X) = (å MmÁ [ X, S m ]) - 1å Mm Y km Á [ X, S m ], (2.6.6)
где Á [ X, S m ] – ядро преобразования, определяемое на основании мер сходства X и S m, а также – статистических предположений о распределении «эталонных» образов { S m, Y m }.
Вопросы для самопроверки к главе 2.
1. Каково назначение ЦАП и АЦП в цифровых системах
управления? Изобразите функциональную схему
одноконтурной цифровой системы управления.
2. Что такое квантователь или ключ? Какое
функциональное преобразование он осуществляет?
3. Как работает ЦАП? Изобразите функциональную схему
ключа и фиксатора (экстраполятора нулевого уровня).
Чему равна передаточная функция экстраполятора?
4. Как выражается z -преобразование сигнала?
5. Как построить z -преобразование передаточной функции
разомкнутой дискретной системы?
6. Как определить отклик дискретной системы на
единичный импульсный входной сигнал, на единичный
ступенчатый входной сигнал?
7. Как определить устойчивость линейной непрерывной
системы с обратной связью по ее непрерывной
передаточной функции П (s)?
8. Как определить устойчивость линейной непрерывной
системы с обратной связью по ее дискретной
передаточной функции П (z)?
9. В чем принципиальная разница по устойчивости между
дискретной и непрерывной системами второго порядка?
10. Как получить дискретную аппроксимацию цифрового
регулятора?
11. Как получить уравнение непрерывной динамической
системы в переменных ее состояния?
12. Как описывается в общем случае состояние линейной
динамической системы в переменных ее состояния?
Приведите векторное описание.
13. Приведите общий вид решения уравнения состояния.
14. Как определяется фундаментальная или переходная
матрица состояния?
15. Выпишите вид линейного и нелинейного уравнений
состояний в дискретно-разностной форме.
16. Объясните смысл и СКО метод идентификации
дискретных моделей линейных систем.
17. Как провести оценку устойчивости дискретно-
разностной модели линейной системы.
18. Приведите функциональную схему системы контроля
качества жидких сред по оптическому светорассеянию.
19. Приведите примеры корреляционных мер сходства.
Чем они отличаются?
20. В чем заключаются методы спектральной
компьютерной квалиметрии?
21. Какие методы получения спектральных данных Вы
знаете?
22. Что лежит в основе теории спектрального анализа?
23. Почему спектры многокомпонентных веществ,
находящихся в конденсированном состоянии носят
нечеткий размытый характер?
24. Какие две проблемы спектральной компьютерной
квалиметрии Вы знаете?
25. Объясните смысл построения экспертных правил в
компьютерной квалиметрии.
Тренировочные задания
1. По аналогии с рис. 1.1.6 нарисуйте блок-схему системы управления температурным режимом водяного котла, учитывая, что необходимо также управлять давлением пара.
2. Покажите, что передаточная функция усилительного звена, связывающего входную величину x и выходную величину y уравнением y = k x, где k – коэффициент усиления, равна
G (s) = k.
3. Покажите, что передаточная функция интегрирующего звена, у которого скорость изменения выходной величины пропорциональна входной величине, т.е. d y /d t = k x, где k – коэффициент усиления, равна
G (s) = k / s.
Изобразите график переходной функции интегрирующего звена, т.е. реакцию на единичную ступенчатую функцию Хевисайда q (t).
4. Воспользовавшись табл. 1.3.1, покажите, что передаточная функция апериодического звена, описываемого дифференциальным уравнением T d y /d t + y = k x, где T – постоянная времени апериодического звена (T > 0), а k – коэффициент его усиления, равна
G (s) = 1 / (Ts + 1).
Покажите, что переходная функция апериодического звена равна
y (t) = k [1– exp(– t / T)].
5. Воспользовавшись табл. 1.3.1, покажите, что передаточная функция колебательного звена, описываемого дифференциальным уравнением W d2 y /d2 t + T d y /d t + y = k x, где (W > 0, T > 0), равна
G (s) = k / (Ws 2 + Ts + 1).
Опираясь на выражение (1.6.10) примера 1.6.1 (стр. 43) изобразите графики всех возможных переходных функций колебательного звена.
6. Покажите, что передаточная функция реального дифференцирующее звено, описываемого дифференциальным уравнением T d y /d t + y = k d x /d t, где (T ³ 0), равна
G (s) = k s / (Ts + 1).
Опираясь на задание 4 покажите, что переходная функция реального дифференцирующего звена равна
y (t) = (k / T) exp(– t / T).
7. Опираясь на формулу Мейсона (1.4.4) и пример 1.4.2 (стр. 30) найдите передаточную функцию сложной системы, описываемой изображенным ниже сигнальным графом.
 |
8. Используя условие устойчивости Рауса-Гурвица
B C – A D > 0
для линейной системы третьего порядка
A y ''' (t) + B y '' (t) + C y '(t) + D y (t) = x (t)
покажите, что предельное значение коэффициента усиления k = = k 1 k 2 k 3 для системы, изображенной ниже на рисунке, имеет значение
k ПР = 2 + T 1/ T 2 + T 1/ T 3 + T 2/ T 1 + T 2/ T 3 + T 3/ T 1 + T 3/ T 2.
 |
8. Используя схему предыдущего задания, покажите, что установившаяся погрешность системы равна
E (s) = X (s) – Y (s) = X (s) / (1 + k) = X (s) STAT,
где STAT = 1/ (1 + k) – коэффициент статизма.
9. Рассчитайте чему равна установившаяся ошибка e ¥ (1.6.7, стр. 42), если N (s) = N 0/ s.
10. Используя правило деления дробей из примера 2.1.2 (см. стр. 52), найдите четыре первых отклика y (0), y (1), y (2) и y (3) выхода дискретной системы на входной импульсный сигнал, если z -образ передаточной функции системы имеет вид
G (z) = 
.
11. Используя пример 2.2.1 (см. стр. 54), выясните – устойчива ли замкнутая дискретная система с передаточной функцией G (z) предыдущего задания?
12. Найдите решение рекуррентного уравнения (2.4.16) для k = 0, 1, 2, 3, если
x (0) = 
, A = 
, B º 0.
13. Используя условия (2.5.9, стр. 63), проверьте устойчивость дискретно-разностной модели yn = a1 yn-1 + a2 yn-2 + a3 yn-3 при следующих значениях ее параметров
a1 = 1; a2 = 0,5; a3 = – 0,7.
14. Выпишите явный вид корреляционных мер сходства (2.6.2 ¸ 2.6.4, стр. 65), используя знак å. Чему равны корреляционных мер сходства при sn * = s = const?
15. Выпишите явный вид модели регрессионной зависимости (2.6.6, стр. 70) для Á [ X, S m ] = exp[ – (X – S m) T F T F (X – S m)].
Тесты по темам модуля
(выбрать правильный ответ/ответы из 3-х предлагаемых)
1. Системой регулирования называется:
1.1 система управления, регулирующая значение выхода;
1.2 система автоматического управления, поддерживающая желаемое значение выходного сигнала;
1.3 система управления, поддерживающая желаемое значение входного сигнала.
2. Принцип обратной связи заключается в том, что:
2.1. в замкнутой системе производится измерение выходной
переменной и его результат в виде сигнала обратной связи
сравнивается с эталонным входным сигналом, несущим
информацию о заданном значении выходной переменной;
2.2. в системе производится измерение выходной переменной и его результат сравнивается с эталонным входным сигналом;
2.3. в системе производится измерение выходной переменной и по результатам сравнивается вырабатывается сигнал обратной связи.
3. Замкнутая система регулирования стремится:
3.1. поддержать заданное соотношение между двумя переменными путем сравнения функций от этих переменных и использования их разности в качестве управляющего сигнала. Чаще всего разность между заданным значением выходной переменной и ее действительным значением усиливается и используется для воздействия на объект управления, в результате чего эта разность постоянно уменьшается;
3.2. поддержать разность между заданным значением выходной
переменной и ее действительным значением;
3.3. усилить разность между заданным значением выходной переменной и ее действительным значением и использовать для воздействия на объект управления, в результате чего уменьшить эту разность.
4. Проектирование систем управления состоит из:
4.1. пяти этапов;
4.2. семи этапов;
4.3. семи этапов и цикла обратной связи.
5. Принцип подобия заключается в:
5.1. применении дифференциальных уравнений к физическим
системам;
5.2. описании однотипными дифференциальными уравнениями
динамики многих непрерывных систем различной физической природы;
5.3. описании подобными дифференциальными уравнениями
систем различной физической природы.
6. Дискретными физическими системами называются системы:
6.1. описываемые дифференциальными уравнениями;
6.2. описываемые алгебраическими уравнениями;
6.3. конечно-разностными уравнениями.
7. Линейная система удовлетворяет свойствам:
7.1. масштабируемости;
7.2. суперпозиции;
7.3. суперпозиции и гомогенности.
8. Переменную s в преобразовании Лапласа можно
рассматривать как:
8.1. алгебраический оператор;
8.2. оператор дифференцирования;
8.3. оператор интегрирования.
9. Оператор 1/ s в преобразовании Лапласа соответствует:
9.1. оператору деления;
9.2. оператору дифференцирования;
9.3. оператору интегрирования.
10. Передаточная функция линейной системы – это:
10.1. отношение преобразования Лапласа выходной переменной к преобразованию Лапласа входной переменной при условии, что все начальные значения равны нулю;
10.2. отношение преобразования Лапласа выходной переменной к преобразованию Лапласа входной переменной;
10.3. преобразование Лапласа отношения выходной переменной к входной переменной при условии, что все начальные значения равны нулю.
11. Характеристическое уравнение замкнутой системы с передаточной функцией объекта G ( s ) и передаточной функцией обратной связи R ( s ) – это:
11.1. 1+ G (s) = 0;
11.2. 1+ G (s) R (s) = 0;
11.3. G (s) R (s) = 0.
12. Передаточная функция замкнутой системы с передаточной функцией объекта G ( s ) и передаточной функцией обратной связи R ( s ) определяется как:
12.1. 1/ R (s);
12.2. G (s) / [1 + G (s) R (s)];
12.3. 1 + G (s) R (s).
13. Сигнальный граф – это:
13.1. диаграмма, состоящая из узлов и отдельных направленных ветвей;
13.2. диаграмма, состоящая из узлов, соединенных между собой отдельными направленными ветвями;
13.3. диаграмма, состоящая из узлов, соединенных между собой ветвями.
13. Путь – это:
13.1. ветвь или последовательность ветвей, которые могут быть проведены от одного узла к другому;
13.2. последовательность ветвей, которые могут быть проведены от одного узла к другому;
13.3. ветвь, проведенная от одного узла к другому.
14. Контур – это:
14.1. замкнутый путь, который начинается и заканчивается в одном и том же узле;
14.2. замкнутый путь, начинающийся и заканчивающийся в
узле;
14.3. замкнутый путь, который начинается и заканчивается в одном и том же узле, причем, вдоль этого пути ни один другой узел не встречается дважды.
15. Система считается оптимальной системой управления,
если:
15.1. ее параметры выбраны таким образом, что оценка качества принимает экстремальное значение;
15.2. ее параметры выбраны таким образом, что оценка качества
принимает минимальное значение;
15.3. ее параметры выбраны таким образом, что принимают
экстремальное (обычно минимальное) значение.
16. ПИД-регуляторы особенно полезны для:
16.1. уменьшений установившейся ошибки и улучшения вида переходной характеристики, когда объект управления
может быть аппроксимирован моделью второго порядка;
16.2. уменьшений установившейся ошибки и улучшения вида переходной характеристики;
16.3. уменьшений установившейся ошибки, когда объект
управления может быть аппроксимирован моделью
второго порядка.
17. Линейная непрерывная система с обратной связью
устойчива, если:
17.1. все полюсы ее передаточной функции П (s) расположены в правой половине s -плоскости;
17.2. все полюсы ее передаточной функции П (s) расположены в левой половине s -плоскости;
17.3. все полюсы ее передаточной функции П (s) расположены в верхней половине s -плоскости.
18. Замкнутая дискретная система устойчива, если:
18.1. все полюсы ее передаточной функции П(z) расположены на z -плоскости вне единичной окружности;
18.2. все полюсы ее передаточной функции П(z) расположены на z -плоскости на единичной окружности;;
18.3. все полюсы ее передаточной функции П(z) расположены на z -плоскости внутри единичной окружности.
19. Элемент jmk ( t ) фундаментальной или переходной матрицы состояний представляет собой:
19.1. реакцию m -ой переменной состояния на начальное значение k -ой переменной состояния;
19.2. реакцию переменной состояния на начальное значение переменной состояния;
19.3. реакцию m -ой переменной состояния на начальное значение k -ой переменной состояния при условии, что начальные значения всех остальных переменных состояния равны нулю.
19. Спектральная компьютерная квалиметрия основана на:
19.1. использовании инструментальных средств оперативного контроля разнообразных физико-химических, оптических, реологических и биологических характеристик пищевых сред совместно с компьютерными экспертными системами;
19.2. связывании с помощью компьютерных экспертных систем спектров (совокупностей) получаемых инструментальных характеристик исследуемых веществ с их соответствующими органолептическими признаками и другими характеристиками, оцениваемыми или инструментально измеряемыми опытными экспертами;
19.3. оценивание или инструментальное измерение разнообразных физико-химических, оптических, реологических и биологических характеристик пищевых сред.
