f (t) = 
, (1.3.2)
где j – мнимая единица (j 2 = – 1), а интегрирование в (1.3.2) проводится по бесконечно удаленному контуру комплексной плоскости для действительного значения переменной s.
Для практического применения используют таблицы преобразований Лапласа (Web-сайт MCS), полученные на основании выражений (1.3.1) и (1.3.2). Пример показан в таблице 1.3.1.
Переменную s в преобразовании Лапласа можно рассматривать как оператор дифференцирования
s º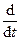 
. (1.3.3)
Аналогично можно ввести оператор интегрирования
. (1.3.4)
Продемонстрируем использование преобразования Лапласа для решения дифференциальных уравнений (типа 2.1.3) с постоянными коэффициентами. Преобразование Лапласа уравнения (2.1.3) дает в соответствии с таблицей 1.3.1
B [ s 2 Y (s)– sy (0)–d y (0)/d t ]+ C [ sY (s)–y(0)] + DY (s) = X (s). (1.3.5)
Если x (t) = 0 (входной сигнал отсутствует), y (0) = y 0 и d y (0)/d t = 0, то
Bs 2 Y (s) – Bs y 0 + CsY (s) – Cy 0 + DY (s) = 0. (1.3.6)
Таблица 1.3.1
| f (t) | F (s) |
| Ступенчатая функция Хевисайда, q (t) | 1/ s |
| Импульсная функция Дирака d (t) | |
tn 
| n!/ sn +1 |
| sin(w t) | w /(s 2 + w 2) |
| cos(w t) | s /(s 2 + w 2) |
| exp(- at) | 1/(s + a) |
| f (k) (t) = d k f (t)/d tk | skF (s)- sk -1 f (0)- sk -2 f’ (0)-…- - sf (k -1)(0) |
| F (s)/ s + (1/ s) 
|
| exp(- at) sin(w t) | w /[(s 2 + a 2) + w 2] |
| exp(- at) cos(w t) | (s + a)/[(s 2 + a 2) + w 2] |
Выражая отсюда Y (s), получим образ выходного сигнала
Y (s) = 
. (1.3.7)
Если полином q (s) = Bs 2 + Cs + D, стоящий в знаменателе (1.3.7), приравнять нулю, то получим характеристическое уравнение, названное так потому, что его корни (или полюса) определяют характер движения системы. Корни полинома p (s) = (Bs + + C) y 0, стоящего в числителе (1.3.7), называют нулями системы. В полюсах функция Y (s) обращается в бесконечность, а в нулях она становится равной нулю. Расположение полюсов и нулей на комплексной s -плоскости определяет характер собственного (свободного) движения системы.
Полином q (s) можно записать в виде
q (s) = (s – s 1) (s – s 2), (1.3.8)
где s 1 и s 2 – корни полинома.
Тогда
Y (s) = 
. (1.3.9)
Пример 1.3.1. Рассмотрим частный случай, когда D / B = 2, а С / B = 3. Тогда выражение (1.3.9) примет вид
Y (s) = 
. (1.3.10)
Положение полюсов и нуля этой функции на s -плоскости показано на рис. 1.3.1, где s = s + jw
 |
Рис. 1.3.1
В общем случае, разложив (1.3.9) на элементарные дроби, получим
Y (s) = 
, (1.3.11)
где k 1 и k 2 – коэффициенты разложения, называемые вычетами.
Теперь применим к (1.3.11) обратное преобразование Лапласа
y (t) = L-1{ }= L-1{ 
}+L-1{ 
}.
(1.3.12)
С помощью таблицы 1.3.1 находим решение
y (t) = k 1exp(s 1 t) + k 2 k 1exp(s 2 t) (1.3.13)
уравнения (2.1.3) в отсутствии входного воздействия, т.е., так называемое, свободное движение системы.
Часто бывает необходимо определить установившееся, или конечное, значение y (t). Теорема о конечном значении гласит, что:
(1.3.14)
где допускается наличие простого полюса Y (s) в начале координат s -плоскости (см. рис. 1.3.1), но не допускается наличие полюсов на мнимой оси и в правой полуплоскости, а также – кратных полюсов в начале координат.
Для примера 1.3.1 
=0. Тем самым, свободное движение стремится к конечному значению y (t) = 0.
Передаточные функции линейных систем.
Передаточная функция линейной системы определяется как отношение преобразования Лапласа выходной переменной к преобразованию Лапласа входной переменной при условии, что все начальные значения равны нулю.
Передаточная функция существует только для линейных стационарных (с постоянными параметрами) систем и однозначно описывает динамическую связь между выходными и входными переменными.
Передаточная функция системы (2.1.3) получается, если в исходном уравнении (1.3.5) все начальные значения положить равными нулю
Bs 2 Y (s) + CsY (s) + DY (s) = X (s). (1.3.15)
Отсюда находим передаточную функцию
(1.3.16)
Пример 1.3.2. Передаточная функция RC цепи, изображенной на рис. 1.3.2, получается путем записи в операторной форме уравнений Кирхгофа для напряжений
U 1(s) = [ R +1/ Cs ] I (s), (1.3.17)
U 2(s) = I (s) / Cs.
 |
Рис. 1.3.2
Тогда из (1.3.17) следует, что
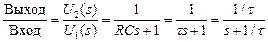, (1.3.18)
где t = RC есть постоянная времени цепи.
Пример 1.3.3. Пусть на вход цепи, изображенной на рис. 1.3.1, подано ступенчатое напряжение c амплитудой U 0 q (t), где q (t) – функция Хевисайда. Как будет изменяться напряжение на выходе цепи?
Так как U 1(s) = U 0/ s (см. таблицу 1.3.1), то согласно (1.3.18)
U 2(s) = U 1(s)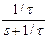 
= U 0 
= U 0[ 
].
В результате обратного преобразования Лапласа получим
u 2(t) = U 0 [1– exp(– t / t)]. (1.3.19)
Рассмотрим теперь поведение системы высокого порядка и найдем ее реакцию на входной сигнал после затухания собственного (свободного) движения.
Пример 1.3.4. Пусть дифференциальное уравнение движения системы имеет вид
y (n) + q n-1 y (n-1) +…+ q 0 y = p n-1 x (n-1) + p n-2 x (n-2) +…+ p 0 x, (1.3.20)
где y (t) есть реакция системы, а x (t) – возмущающая функция.
Если все начальные значения равны нулю, то вместо дифференциального уравнения (1.3.20) системы запишем его образ по Лапласу
s n Y (s) + q n-1 s n-1 Y (s) +…+ q 0 = (1.3.21)
= p n-1 s n-1 X (s) + p n-2 s n-2 X (s) +…+ p 0 X (s).
Тогда реакция системы состоит из свободного движения, определяемого начальными условиями, и вынужденного движения, обусловленного входным возмущением
Y (s) = 
, (1.3.22)
