
Ряд сходится при 

(-1;1)- интервал сходимости ряда
Исследуем ряд на сходимость на концах интервала
При х=-1 получаем следующий ряд:

Знакочередующийся ряд
Проверим на сходимость по признаку Лейбница.
1)




……….

Ряд сходится по признаку Лейбница
При х=1 получаем следующий ряд:

Числовой ряд проверим на сходимость по второму признаку сравнения рядов.
Будем сравнивать с гармоническим рядом.

гармонический ряд является расходящимся рядом.
 =
= 
 =
=  =
=  =
= 
=  конечное число.
конечное число.
Оба ряда одновременно расходятся.
 область сходимости степенного ряда
область сходимости степенного ряда
Пример 6.7.Найдите область сходимости степенного ряда

Степенной ряд



=  =
=  =
=
=  =
=  =
=
=  =
=  =
=  =
= 
Ряд сходится при 



(-5;-3)- интервал сходимости ряда
Исследуем ряд на сходимость на концах интервала
При х=-5 получаем следующий ряд:
 =
= 
Знакочередующийся ряд
Проверим на сходимость по признаку Лейбница.
1)




……….

Ряд сходится по признаку Лейбница
При х=-3 получаем следующий ряд:
 =
= 

Числовой ряд проверим на сходимость по второму признаку сравнения рядов.
Будем сравнивать с гармоническим рядом.

гармонический ряд является расходящимся рядом.
 =
= 
 =
=  =
=  =
=
=  =
=  =1 конечное число.
=1 конечное число.
Оба ряда одновременно расходятся.
 область сходимости степенного ряда
область сходимости степенного ряда
Пример 6.8. Вычислить интеграл с точностью до 0,001:






Пример 6.9.Разложите данную функцию f(x) в ряд Тейлора в окрестности точки x0 (выпишете первых три ненулевых члена ряда):
 .
.
Решение. Ряд Тейлора имеет следующий вид

Далее находим

| 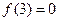
| |||

| 
| |||
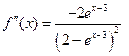
| 
| |||

| 
| |||
Таким образом, первых три ненулевых члена ряда Тейлора исходной функции будут иметь следующий вид
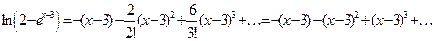
Пример 6.10. Разложите данные функции в ряд Маклорена, используя разложения для функций cosx, sinx, ex, ln(1+x), (1+x)m, arctgx:
а)  , ,
| б)  . .
|
Решение. а) В данном случае воспользуемся разложением

Тогда

и
 .
.
Окончательно получаем
 .
.
б) В данном случае воспользуемся биномиальным разложением

В данном случае

Тогда

Таким образом, искомое разложение будет иметь вид

Итоговая контрольная работа №1 по темам 1,2,3
Вариант 1
1. Вычислить пределы:
а) 
| г) 
|
б)  в)
в) 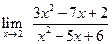 , ,
| д)  е)
е) 
|
2. Построить график и определить характер точек разрыва:
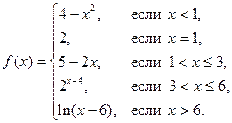
3. Найти производные dy/dx данных функций:
а) 
| б) 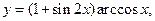
|
г) 
| д)  , ,
|
в)  , ,
| |
е)  . .
|
4. Найти наибольшее и наименьшее значения функции
y = x–2 
на отрезке [0;4].
5. Вычислить пределы, используя правило Лопиталя:
а) 
| б)  . .
|
6. Исследовать функцию методами дифференциального исчисления и, используя результаты исследования, построить ее график:
 .
.
7. Найти все частные производные 1-го порядка:
а) 
| б) 
|
в)  .
.
8. Дана функция  . Показать, что
. Показать, что  .
.
9. Найти наименьшее и наибольшее значения функции  в замкнутой области D:
в замкнутой области D:  .
.
10. Дана функция  , точка A(1;3) и вектор
, точка A(1;3) и вектор  . Найти: a)
. Найти: a)  в точке A; б) производную в точке A по направлению вектора a.
в точке A; б) производную в точке A по направлению вектора a.
Вариант 2
1. Вычислить пределы:
а) 
| б) 
| |
г) 
| д) 
| |
в) 
| ||
е) 
| ||
2. Построить график и определить характер точек разрыва:

3. Найти производные dy/dx данных функций:
а) 
| б) 
|
г) 
| д)  , ,
|
в) 
| |
е)  . .
|
4. Найти наибольшее и наименьшее значения функции 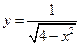 на отрезке [–1;1].
на отрезке [–1;1].
5. Вычислить пределы, используя правило Лопиталя:
а) 
| б)  . .
|
6. Исследовать функцию методами дифференциального исчисления и, используя результаты исследования, построить ее график:
 .
.
7. Найти все частные производные 1-го порядка:
а) 
| б) 
|
в)  .
.
8. Дана функция  . Показать, что
. Показать, что  .
.
9. Найти наименьшее и наибольшее значения функции  в замкнутой области D:
в замкнутой области D:  .
.
10. Дана функция  , точка A(–1;2) и вектор
, точка A(–1;2) и вектор  . Найти: a)
. Найти: a)  в точке A; б) производную в точке A по направлению вектора a.
в точке A; б) производную в точке A по направлению вектора a.
Итоговая контрольная работа №2 по теме4
Вариант 1
1. Найти общий или частный интеграл (решение) дифференциального уравнения первого порядка:
а)  , ,
|
б) 
|
в)  , ,
|
г)  , ,
|
д) 
|
е) 
|
2. Найти общий или частный интеграл (решение) дифференциального уравнения, допускающего понижения порядка:
а) 
б)  .
.
3. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка:
а) 
|
б)  в)
в) 
|
Вариант 2
1. Найти общий или частный интеграл (решение) дифференциального уравнения первого порядка:
а)  , ,
|
б) 
|
в)  , ,
|
г)  , ,
|
д) 
|
е) 
|
2. Найти общий или частный интеграл (решение) дифференциального уравнения, допускающего понижения порядка:
а) 
б) 
3. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка:
а) 
|
б) 
|
в) 
|






