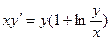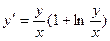У=кх+в
К= 
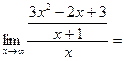
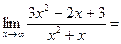
в=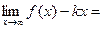 
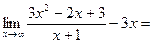
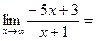
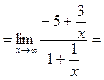
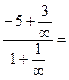
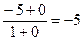
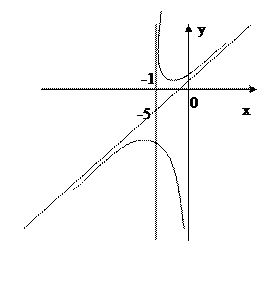
У=3х-5–наклонная асимптота
Вертикальные асимптоты
Х=1 точка разрыва
= 
= 
= 
= 
= 
= 
= 
= 
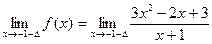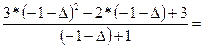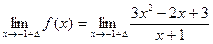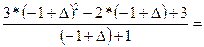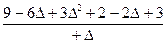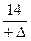Пример 2.11.
Вычислить предельную выручку, если известны уравнения спроса10q+p-100=0 и значения цены р=80 на продукцию (- количество продукции. р-цена продукции) Что она показывает?
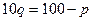
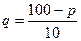
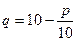
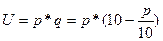
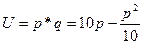
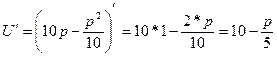
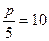
оптимальная цена, при которой получаем максимальную выручку и при которой спрос равен передложению
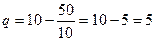Количество товара, которое можно продать с учетом спроса при оптимальной цене.
Пример 2.12.
Функции спроса и предложения имеют вид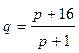 
- спроса, 
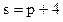- предложения.
Найти: 1) равновесную цену 
;
2) эластичность спроса и предложения для этой цены .
1) равновесная цена находится в случае, если спрос равен предложению
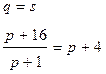
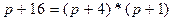
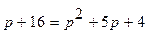
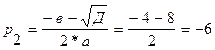
оптимальная цена, при которой получаем максимальную выручку и при которой спрос равен передложению
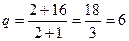Количество товара, которое можно продать с учетом спроса при оптимальной цене.
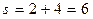Спрос на товар по оптимальной цене
2) эластичность спроса и предложения для этой цены .
Эластичностью функции f(x) в точке x0 называют предел
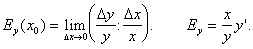
Спрос – это количество товара, востребованное покупателем. Ценовая эластичность спроса ED – это величина, характеризующая то, как спрос реагирует на изменение цены. Если |ED| > 1, то спрос называется эластичным, если |ED| < 1, то неэластичным. В случае ED = 0 спрос называется совершенно неэластичным, т. е. изменение цены не приводит ни к какому изменению спроса. Напротив, если самое малое снижение цены побуждает покупателя увеличить покупки от 0 до предела своих возможностей, говорят, что спрос является совершенно эластичным. В зависимости от текущей эластичности спроса, предприниматель принимает решения о снижении или повышении цен на продукцию.
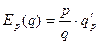
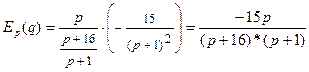
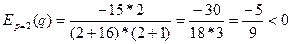
Тема 3: «Дифференциальное исчисление функции нескольких переменных»
Пример 3.1.
Найти все частные производные 1-го порядка: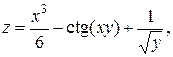 
Пример 3.2.
Найти все частные производные 1-го порядка
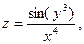
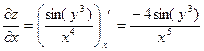
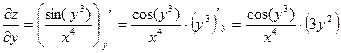
Пример 3.3.
Найти все частные производные 1-го порядка
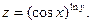
Пример 3.4.
Найти все частные производные 2-го порядка
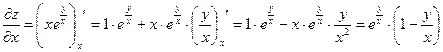
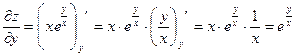
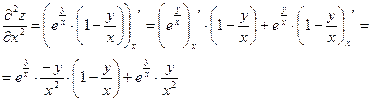
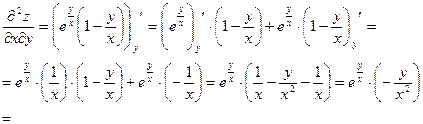
Пример 3.5.
Дана функция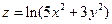 
, точка A(1; 1) и вектор 
.
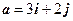Найти: a) 
в точке A; б) производную в точке A по направлению вектора a.
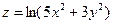
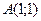
Найдем частные производные данной функции
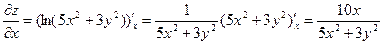
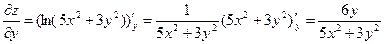
Подставим координаты точки А в данные частные производные.
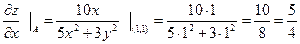
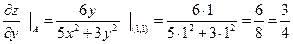
в точке A
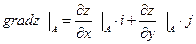
Определим направляющие косинусы для вектора а
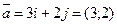
Для этого найдем длину вектора
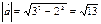
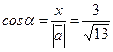
Найдем производную по направлению
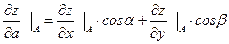
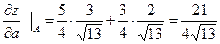
Пример 3.6.
Докажите, что функция 
удовлетворяет уравнению 
.
Решение:
Найдем частные производные данной функции
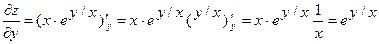
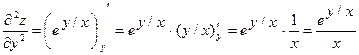
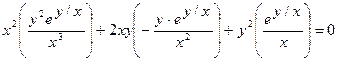
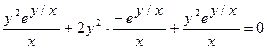
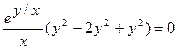
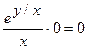
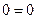
Пример 3.7.
Производственная деятельность фирмы описывается функцией Кобба-Дугласа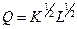 
, где 
- величина выпуска продукции,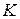 
- число единиц оборудования (капитал) и 
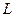- численность работающих (труд).
1) Составьте функцию издержек фирмы, если стоимость ед. фактора 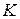равна 4 ден.ед., а стоимость ед. фактора 
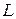равна 1 ден.ед.
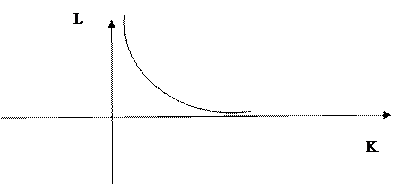
2) Решите задачу определения максимального выпуска продукции, который может обеспечить фирма, полностью истратив все средства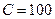 
ден.ед.
Решение:
Функция издержек фирмы
ден. ед.
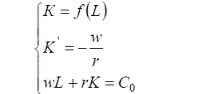
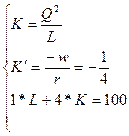
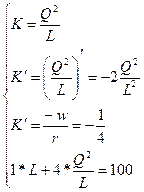
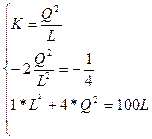
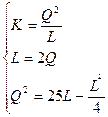
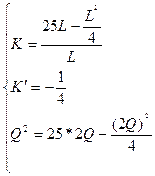
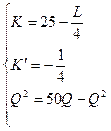
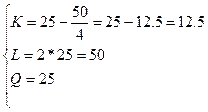
Изокванта для выпуска продукции объемом Q (4, 1)=2
 |
К= 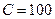ден.ед.
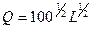
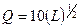
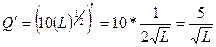
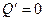
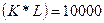
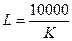
| K | ||||
| L |
Пример 3.8.
Фирма реализует произведенную продукцию по цене p, а зависимость издержек C имеет вид 
.
a=15; b=0,009; c=100; p=85.
1) выполнить полное исследование функции зависимости прибыли фирмы П от объема производства q построить ее график;
2) найти оптимальный для фирмы объем выпуска продукции и соответствующую ему прибыль.
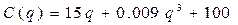
Прибыль= доход- издержки
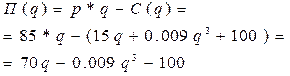
Общая схема исследования:
1. Область определения
2. Точки пересечения с осями координат
3. Четность-нечетность, периодичность.
4. Точки экстремума, промежутки возрастания, убывания функции.
5. Точки перегиба, промежутки выпуклости, вогнутости.
6. Асимптоты вертикальные и наклонные.
7. График.
1) Область определения
Д(q)=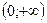 
2) Точки пересечения с осями координат
С ось ох =>у=0
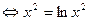нет корней
Нет точек пересечения с осями координат
3)Четность-нечетность, периодичность
Д(q)=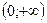
Так как график несимметричен относительно оси оу и начала координат, нечетная и не нечетная
Функция не содержит тригонометрических выражений - не является периодической.
4)Точки экстремума, промежутки возрастания, убывания.
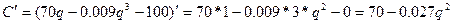
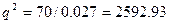
q=50.92- точка экстремума
убыток
| q | (0;50,92) | 50,92 | (50,92;  )
| |
| + | - | ||
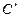
| C | -100 | возрастает | 2275,3 | убывает |
5)Точки перегиба, промежутки выпуклости, вогнутости
| q |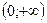
| |
|
| - | |
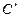
| C | -100 | выпукла |
6) Асимптоты
У=кх+в
|
|
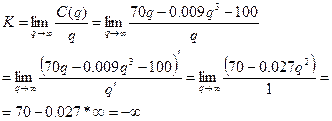
П=2275,3 прибыль
Тема 4: «Интегральное исчисление»
Пример 4.1. Вычислить интеграл непосредственным интегрированием:
Пример 4.2 Вычислить интеграл методом замены: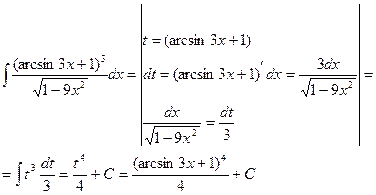 
;
Пример 4.3 Вычислить интеграл методом интегрирования по частям: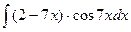 
.
При вычислении данного интеграла воспользуемся формулой интегрирования по частям
.
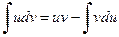Тогда получим
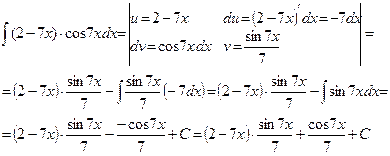
Пример 4.4. Найти неопределённый интеграл с помощью замены переменной:
= 
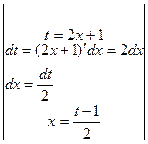
Пример 4.5. Найти неопределённый интеграл с помощью замены переменной:
.= 
= 
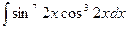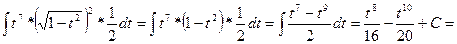
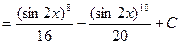
Пример 4.6. 
Разложим подынтегральную функцию, т.е. правильную рациональную дробь, на сумму простейших дробей:
.
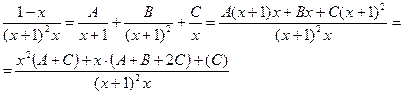Приведем правую часть равенства к общему знаменателю и приравняем числители левой и правой частей:
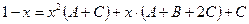
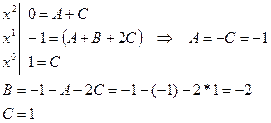
Таким образом,
.
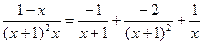Далее, вычисляем исходный интеграл
Пример 4.7.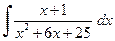 
,
Пример 4.8. Найти площадь фигуры, ограниченной линиями:
Найдем точки пересечения
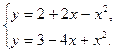
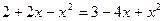
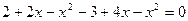
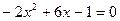
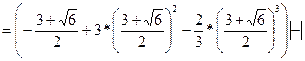
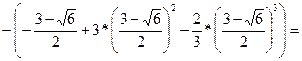
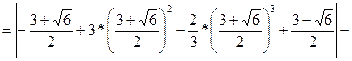
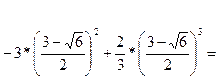
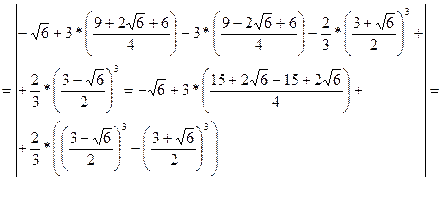
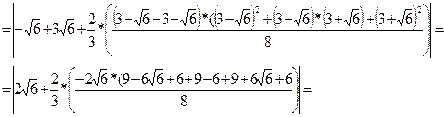
кв.ед.
Ответ: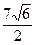 
кв.ед.
Пример 4.7. 
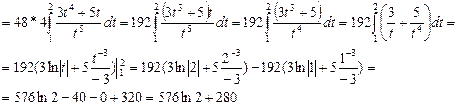
Пример 4.8.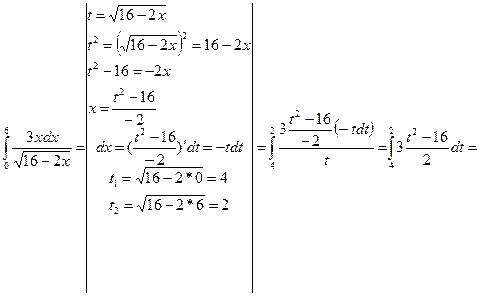 
= 
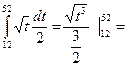
Пример 4.9.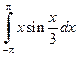 
.
= 
= 
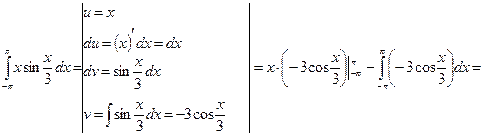
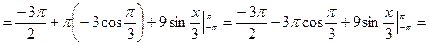
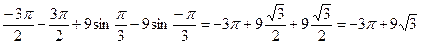
Пример 4.10. Вычислить несобственный интеграл или установить его расходимость:
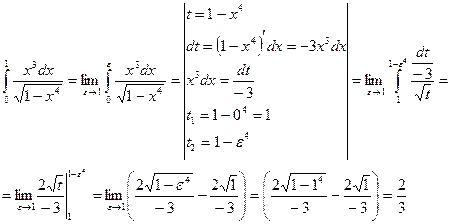
Пример 4.11.
Найти среднее время, затраченное на освоение одного изделия в период освоения от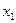 
до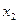 
изделий, если известна функция 
,описывающая изменение затрат времени t на изготовление изделия в зависимости от степени освоения производства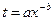 
|
|
| 
| 
|
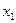
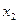
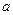
| 0,5 |
Найти среднее время, затраченное на освоение одного изделия в период освоения от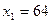 
до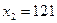 
изделий, используя формулу
,
полагая в формуле 
, где 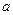– затраты времени на первое изделие, – показатель производственного процесса,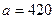 
(мин.), 
.
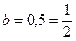Решение:
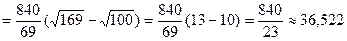(мин.).
Тема 5: «Дифференциальные уравнения»
Пример 5.1. Найти общее решение или общий интеграл дифференциального уравнения:
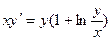
Данное уравнение является однородным уравнением 
