Пусть СМО содержит один канал. Поток заявок является простейшим с интенсивностью l. Время обслуживания Тобсл распределено по произвольному закону с математическим ожиданием 
= M[Тобсл] и средним квадратическим отклонением sобсл = 
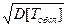Такая система не является марковской, так как поток обслуживания не является простейшим.
Можно доказать, что среднее число заявок, находящихся в очереди, и среднее время ожидания обслуживания вычисляются по формулам Полячека—Хинчина:
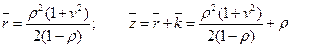(29)
где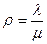 
коэффициент загрузки системы; v = sобсл ×m- коэффициент вариации времени обслуживания.
Из (29) по формулам Литтла получим:
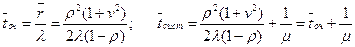(30)
Задача 7. На контейнерную площадку с одним краном прибывает простейший поток автомашин со средним интервалом между ними, равным 10 мин. Время погрузки-выгрузки в среднем составляет 6 мин. Время погрузки-выгрузки распределено по произвольному закону, среднее квадратическое отклонение времени погрузки-выгрузки равно 1 мин. Определить:
1) среднее число автомашин, ожидающих погрузки-выгрузки;
2) средний простой машин в ожидании погрузки-выгрузки;
3) среднее число автомашин на контейнерной площадке;
4) среднее время нахождения машины на контейнерной площадке.
Решение. Контейнерную площадку с одним краном можно рассматривать как одноканальную СМО с неограниченной очередью, простейшим входящим потоком и произвольным распределением времени обслуживания. Найдем параметры СМО: l = 1/M[T} = 1/10 = 0,1 (машин в мин), m = 1/ M[Тобсл] = 1/6 = 0,167 (машин в мин);
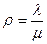» 0,1/0,167» 0,599; v = v = sобсл ×m = 1 × 0,167.
По формулам (29) и (30) вычислим показатели работы СМО:
1) среднее число автомашин, ожидающих погрузки-выгрузки:
0,459 маш;
2)средний простой машин в ожидании погрузки-выгрузки:
0,459 / 0,1 = 4,59» 4,6 мин;
3)среднее число автомашин на контейнерной площадке:
» 0,459 + 0,599 =1,058 маш.;
4)среднее время нахождения машины на контейнерной площадке:
4,59 + 6» 10,6 мин.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Гмурман В. Е. Теория вероятностей и математическая статистика. М.; Высшая школа, 1999.
2. В е н ц е л ь Е.С. Исследование операций: задачи, принципы методология. М.: Наука, 1998.
3. Чистяков В. П, Курс теории вероятностей. М.: Наука, 1972.
4. Д а н к о П.Е., П о п о в А.Г., К о ж е в н и к о в а Т.Я. Высшая математика в упражнениях и задачах. Ч. 2. М.: Высшая школа, 1986.
5. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 1999.
6. С и н д а л о в с к и й Г.Х. Высшая математика. Основные понятия теории вероятностей. Учебное пособие. М.: РГОТУПС, 1997.
7. М а л ы ш е в а И. А. Теория вероятностей и массового обслуживания: Рабочая программа, методические указания и контрольные задания для студентов-заочников 2 курса специальности УПП. М.: ВЗИИТ, 1991.
8. Г у ш е л ь Н.П. Начальные понятия комбинаторики: Учебное пособие. М.: ВЗИИТ, 19 92.
9. Г у ш е л ь Н.П. Математика. Рабочая программа и задания на контрольные работы N 6 – 9 для студентов 2 курса всех инженерно – технических специальностей.
М.: РГОТУПС, 2000.
Содержание:
Теория массового обслуживания.
Случайные процессы.
Поток событий.
Нестационарный пуассоновский поток.
Поток Пальма.
Потоки Эрланга.
Цепи Маркова.
Матрица переходов и граф состояний.
Предельные вероятности.
Марковские цепи с конечным числом состоянии и непрерывным временем
Процесс гибели и размножения
Системы массового обслуживания и их классификация.
Марковские системы массового обслуживания
Показатели эффективности систем массового обслуживания
Замкнутые системы массового обслуживния
Открытые системы массового обслуживания
Таблица основных формул для открытых СМО
Одноканальная система с произвольным распределением времени обслуживания
Литература
