Здесь рассматриваются СМО, у которых, входящий поток пуассоновский, а время обслуживания — показательное.
Многоканальная система массового обслуживания с ограниченной очередью





 l l … l l l … l l
l l … l l l … l l











 А0 А1 Аk Аk+1 Аk+m-1 Аk+m
А0 А1 Аk Аk+1 Аk+m-1 Аk+m

 m 2m … km km km … km km
m 2m … km km km … km km
Рис. 6
Пусть СМО содержит k каналов, число мест в очереди – m (длина очереди), входящий поток заявок имеет интенсивность l, поток обслуживания заявки одним каналом имеет интенсивность m. Будем нумеровать состояния СМО по числу занятых каналов:
А0— все каналы свободны; А1 — один канал занят;......; Ai - i каналов занято, (k—i) каналов свободны;......; Ak— все каналы заняты; Ak+1— все каналы заняты, одна заявка в очереди; …; Ak+m— все каналы заняты, m заявок в очереди.
Размеченный граф состояний имеет вид, представленный на рис.6. Сравнивая рисунки 6 и 3, приходим к выводу, что граф на рис. 6 является графом процесса гибели и размножения, для которого:
li = l, mi = m. (18)
Тогда предельное распределение вероятностей состояний можно вычислить по формулам (11). Обозначая через 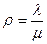 (коэффициент загрузки системы), с учетом соотношений (18) из (11) получим:
(коэффициент загрузки системы), с учетом соотношений (18) из (11) получим:
p0 =  ;
;
p1 =  p0; p2 =
p0; p2 = 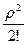 p0; …; pk =
p0; …; pk =  p0; pk+1 =
p0; pk+1 =  p0; …; pk+m =
p0; …; pk+m =  p0. (19)
p0. (19)
Обозначим  . Применяя формулу суммы ряда геометрической прогрессии, получим:
. Применяя формулу суммы ряда геометрической прогрессии, получим:
p0 = 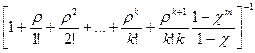 (20)
(20)
С помощью формул (19), (20) вычисляются показатели эффективности СМО:
А = ( )m =
)m =  = l(1 – pk+m); Q =
= l(1 – pk+m); Q =  = 1 – pk+m; Pотк = 1 – Q = pk+m;
= 1 – pk+m; Pотк = 1 – Q = pk+m;  (1 – pk+m);
(1 – pk+m);  ;
; 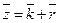 (21)
(21)
Для открытых СМО справедливы соотношения:
 =
=  ,
, 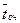 =
=  и
и 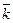 =
=  . (17)
. (17)
где l — интенсивность потока заявок, m — интенсивность потока обслуживания. Формулы (17) справедливы только в том случае, когда входящий поток заявок и поток обслуживания стационарны.
(Первая и вторая формулы называются формулами Литтла.)
Рассмотрим частные случаи:
1. Многоканальная система массового обслуживания с отказами (задача Эрланга).
Пусть m = 0, т.е. очередь не допускается, если все каналы обслуживания заняты, то заявка покидает СМО. Из формул (20), (21) получим:
p0 =  ;
;
p1 =  p0; p2 =
p0; p2 = 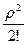 p0; …; pk =
p0; …; pk =  p0. (22)
p0. (22)
Формулы (22) называются формулами Эрланга.
А = l(1 – pk); Q = 1 – pk; Pотк = pk;  (1 – pk); (23)
(1 – pk); (23)
Задача 4. Диспетчерская служба имеет 5 линий связи. Поток вызовов простейший с интенсивностью l=0,8 вызовов в минуту. Среднее время переговоров с диспетчером составляет t = 3 мин. Время переговоров распределено по показательному закону. Найти 1) абсолютную и относительную пропускные способности диспетчерской службы; 2) вероятность отказа; 3) среднее число занятых каналов. Определить, сколько линий связи должна иметь диспетчерская служба, чтобы вероятность отказа не превышала a = 0,01?
Решение. Находим интенсивность потока обслуживания m = 1/ M[Tобсл] = 1/3 разговора в минуту. Коэффициент загрузки СМО составляет r =  =
=  = 2,4. Из формул (22) при k = 5 имеем:
= 2,4. Из формул (22) при k = 5 имеем:
p0=  =
= 
 [10,629]-1
[10,629]-1  0,094;
0,094;
p5 = 

= 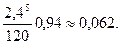
Находим по формулам (23):
а) абсолютная пропускная способность:
А = l(1—р5)  0,8 (1—0,062)
0,8 (1—0,062)  0,8.0,938
0,8.0,938  0,750.
0,750.
(следовательно, СМО обслуживает в среднем 0,75 заявки в минуту);
б) относительная пропускная способность:
Q = 1 – p5 = 1 - 062  0,938
0,938
(следовательно, вероятность обслуживания вновь поступившей заявки равна 0,938);
в) вероятность отказа: Pотк = p5 = 0,062;
г) среднее число занятых каналов:
 = 2,4.0,938
= 2,4.0,938  2,251
2,251
(следовательно, диспетчерская служба в среднем имеет половину линии связи постоянно занятыми).
Поскольку вероятность отказа данной диспетчерской службы pотк - 0,062 превышает 0,01, то число линий связи следует увеличить. Допустим, что линий связи стало 6. Тогда из формул (22) при k=6
P0 = [10,629 + 0.265]-1  0,092;
0,092;
p6 =  092 = 0,265.0,092
092 = 0,265.0,092  0,024 >0,01.
0,024 >0,01.
Следовательно, при k=6 вероятность отказов Ротк = Р6 = 0,024 превышает 0,01. Значит, число каналов надо увеличить. При k=7 получим: p0 = 0,091; p7 = 0,008. Следовательно, при k =7 вероятность отказов Ротк =p7 = 0,008 не превышает 0,01. Таким образом, для обеспечения требуемой вероятности отказов следует увеличить количество линий связи диспетчерской службы до 7.
Многоканальная система массового обслуживания с неограниченной очередью
Пусть СМО имеет k каналов обслуживания. Все потоки простейшие. Интенсивность потока заявок —l, потока обслуживания одной заявки — m. Коэффициент загрузки СМОr=  . Обозначим отношение коэффициента загрузки к числу каналов в системе черезc =
. Обозначим отношение коэффициента загрузки к числу каналов в системе черезc =  . Предельноераспределение вероятностей состояний в описываемой СМО существует только при c<1. Этот факт можно объяснить, если рассматривать данную СМО как предельный случаи многоканальной СМО с ограниченной очередью при стремлении длины очереди к бесконечности. Тогда предельное распределение вероятностей состояний можно вычислить как предел при т—>¥ предельных вероятностей (19)- (20). При этом возникает бесконечный числовой ряд, состоящий из членов геометрической прогрессии, который сходится, если знаменатель прогрессии меньше 1, т. е. c<1, и имеет сумму
. Предельноераспределение вероятностей состояний в описываемой СМО существует только при c<1. Этот факт можно объяснить, если рассматривать данную СМО как предельный случаи многоканальной СМО с ограниченной очередью при стремлении длины очереди к бесконечности. Тогда предельное распределение вероятностей состояний можно вычислить как предел при т—>¥ предельных вероятностей (19)- (20). При этом возникает бесконечный числовой ряд, состоящий из членов геометрической прогрессии, который сходится, если знаменатель прогрессии меньше 1, т. е. c<1, и имеет сумму  .
.
Обозначим через pi предельную вероятность того, что в системе занято i каналов (0< i < k+1), а через pk+r — предельную вероятность того, что в системе заняты все k каналов и r заявок стоят в очереди. При c<1 предельное распределение вероятностей состояний имеет вид:
p0 =  ;
;
pi = 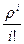 p0; (0< i < k+1); pk+r =
p0; (0< i < k+1); pk+r =  p0; (r > 0). (23)
p0; (r > 0). (23)
Так как очередь в СМО не ограничена, то каждая заявка рано или поздно будет обслужена, следовательно, справедливы соотношения
Pотк = 0, Q = 1 – Pотк = 1, A = Q l = l. (24).
Остальные показатели эффективности СМО вычисляются по формулам:
 ;
;  ;
;  ;
;
 =
=  ;
; 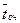 =
=  . (25)
. (25)
Таблица основных формул для открытых СМО
| № | Общий случай (m – число мест в очереди) | Задача Эрланга (m = 0) | Неограниченное число мест в очереди (m = ¥),  <1 <1
|
p0 =  pi = pi = 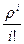 p0;(0< i £k);pk+r= p0;(0< i £k);pk+r=  p0;(1£r £m). p0;(1£r £m).
| p0 =  pi = pi = 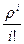 p0;(0< i £ k). p0;(0< i £ k).
| p0 =  pi =
pi = 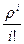 p0; (0< i £ k); pk+r = p0; (0< i £ k); pk+r =  p0; (r > 0). p0; (r > 0).
| |
А = ( )m = )m =  = l(1 – pk+m) — среднее число заявок, обслуживаемое СМО в единицу времени. Эту характеристику называютабсолютной пропускной способностью СМО. = l(1 – pk+m) — среднее число заявок, обслуживаемое СМО в единицу времени. Эту характеристику называютабсолютной пропускной способностью СМО.
| А =l(1 – pk) | А =l | |
Q =  = 1 – pk+m
- вероятность обслуживания поступившей заявки или относительная пропускная способность СМО. = 1 – pk+m
- вероятность обслуживания поступившей заявки или относительная пропускная способность СМО.
| Q = 1 – pk | Q = 1 | |
| Pотк = 1 – Q = pk+m — вероятность отказа, т. е. вероятность того, что поступившая заявка не будет обслужена | Pотк = pk | Pотк = 0 | |
 (1 – pk+m)
— среднее число занятых каналов. (1 – pk+m)
— среднее число занятых каналов.
|  (1 – pk) (1 – pk)
| 
| |
 — среднее число заявок в очереди.
— среднее число заявок в очереди.
| 
| ||
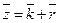 - среднее число заявок в СМО (имеются в виду все заявки, как обслуживаемые, так и ожидающие очереди, если они есть).
- среднее число заявок в СМО (имеются в виду все заявки, как обслуживаемые, так и ожидающие очереди, если они есть).
|  r(1 – pk) r(1 – pk)
| 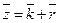 = r + = r + 
| |
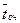 = =  среднее время пребывания заявки в очереди.
среднее время пребывания заявки в очереди.
| 
| ||
 = =  - среднее время пребывания заявки в СМО, как в очереди, если она есть, так и под обслуживанием.
- среднее время пребывания заявки в СМО, как в очереди, если она есть, так и под обслуживанием.
|  = =  (1 – pk) (1 – pk)
|  = = 
|
Пример. Дисплейный зал имеет k дисплеев. Поток пользователей простейший. Среднее число пользователей, посещающих дисплейный зал за сутки, равно п. Время обработки информации одним пользователем на одном дисплее распределено по показательному закону и составляет в среднем t мин. Определить, существует ли стационарный режим работы зала; вероятность того, что пользователь застанет все дисплеи занятыми; среднее число пользователей в очереди; среднее время ожидания свободного дисплея; среднее время пребывания пользователя в дисплейном зале.
Дано: k=2, n=40, t=34
Решение: Рассматриваемая в задаче СМО относится к классу многоканальных систем с неограниченной очередью. Число каналов k=2. Найдем  - интенсивность потока заявок:
- интенсивность потока заявок:  , где
, где  - среднее время между двумя последовательными заявками входящего потока пользователей. Тогда
- среднее время между двумя последовательными заявками входящего потока пользователей. Тогда  . Найдем
. Найдем  - интенсивность потока обслуживания:
- интенсивность потока обслуживания:  , где
, где  - среднее время обслуживания одного пользователя одним дисплеем, тогда
- среднее время обслуживания одного пользователя одним дисплеем, тогда  . Таким образом, классификатор данной системы имеет вид СМО
. Таким образом, классификатор данной системы имеет вид СМО 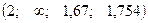 .
.
Вычислим коэффициент загрузки СМО  . Известно, что для СМО такого класса стационарный режим существует, если отношение коэффициента загрузки системы к числу каналов меньше единицы.
. Известно, что для СМО такого класса стационарный режим существует, если отношение коэффициента загрузки системы к числу каналов меньше единицы.
Находим это отношение  .
.
Следовательно, стационарный режим существует. Предельное распределение вероятностей состояний вычисляется по формулам:

Поскольку k=2, имеем:

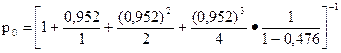

Вычислим  - вероятность того, что пользователь застанет все дисплеи занятыми. Очевидно, она равна сумме вероятностей таких событий: все дисплеи заняты, очереди нет (p2); все дисплеи заняты, один пользователь в очереди (p3); и так далее. Поскольку для полной группы событий сумма вероятностей этих событий равна единицы, то справедливо равенство
- вероятность того, что пользователь застанет все дисплеи занятыми. Очевидно, она равна сумме вероятностей таких событий: все дисплеи заняты, очереди нет (p2); все дисплеи заняты, один пользователь в очереди (p3); и так далее. Поскольку для полной группы событий сумма вероятностей этих событий равна единицы, то справедливо равенство  .
.
Найдем эти вероятности: 

Используя формулы для вычисления показателей эффективности, найдем:
1) среднее число пользователей в очереди
 ;
;
2) среднее число пользователей в дисплейном зале
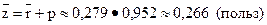 ;
;
3) среднее время ожидания свободного дисплея
 ;
;
4) среднее время пребывания пользователя в дисплейном зале

Ответ: стационарный режим работы дисплейного зала существует и характеризуется следующими показателями  ;
;  пользователя;
пользователя;  пользователя;
пользователя;  мин;
мин;  мин.
мин.






