Антенним фідером називається пристрій для передачі високочастотної енергії від передавача до антени, або від антени до приймача. Вимоги, що висуваються до фідера:
1) Мінімальні втрати енергії високочастотних коливань на нагрів провідників й діелектриків, а також на випромінювання.
2) Відсутність антенного ефекту, тобто сам фідер не має випромінювати та приймати електромагнітні хвилі.
3) Відсутність впливу на частоту настройки вихідного контура передавача, або вхідного контура приймача.
4) Можливість передачі заданої потужності високочастотних коливань.
5) Стабільність електричних параметрів і механічна надійність.
Найпростішим за конструкцією фідером можна вважати повітряну однопровідну лінію, в якій оберненим проводом служить земля (рис. 10.1). За визначенням хвильовий опір довільної лінії 
, де L i C - погонні індуктивність і ємність провідників лінії.
Рис. 10.1
Застосування цього визначення до однопровідної лінії дозволяє знайти наступний вираз для розрахунку її хвильового опору через геометричні розміри:
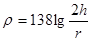. (10.1)
На практиці однопровідний фідер використовується рідко через властивий йому недолік - значний антенний ефект.
Меншим антенним ефектом володіють двопровідні лінії (рис. 10.2). Мідні або біметалеві провідники двопровідної лінії діапазону декаметрових хвиль вибираються діаметром 3-6 мм і
розташовуються на відстані 20-40 см. Хвильовий опір двопровідного фідера становить:
. (10.2)
Чотирипровідна лінія пониженого хвильового опору, поперечний переріз якої показано на рис. 10.3, складається зі з’єднаних попарно чотирьох провідників. Її хвильовий опір можна обчислити за формулою:
. (10.3)
Незначним антенним ефектом володіє чотирипровідна лінія з діагонально з’єднаними провідниками (рис. 10.4). При розташуванні провідників лінії у вершинах квадрата її хвильовий опір становить:
. (10.4)
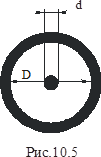
Екранований фідер у вигляді лінії концентричного типу (коаксіальний кабель) практично вільний від антенного ефекту, захищений від атмосферних впливів і зручний для монтажу. Поперечний переріз коаксіальної лінії показано на рис. 10.5, а її хвильовий опір розраховується за формулою (10.5):
. (10.5)
В останньому виразі k - коефіцієнт вкорочення хвилі. За визначенням k=l0/l, де l0 - довжина хвилі у вакуумі, l - довжина хвилі у фідері. Коефіцієнт вкорочення хвилі для коаксіального фідера залежить від відносної діелектричної проникності e ізоляції і коефіцієнта заповнення ізоляцією простору між провідниками фідера А:
. (10.6)
Для кабеля із суцільною ізоляцією А=1 і тому 
. Вкорочення довжини хвилі є наслідком її меншої швидкості розповсюдження в кабелі у порівнянні з вільним простором: v=c/k.
Для практики корисно нагадати наступні співвідношення:
, 
, 
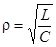. (10.7)
Втрати енергії у фідері залежать не тільки від його конструкціїї, але й від електричного режиму роботи. Нехай фідер довжиною l працює в режимі біжучої хвилі. Режим біжучої хвилі реалізується за умови, що хвильовий опір лінії рівний активному вхідному опору антени (r = RА), а реактивний опір антени дорівнює нулю (XА = 0). При цьому в ідеальній лінії без втрат енергії амплітудне значення високочастотної напруги між провідниками лінії залишається незмінним по всій її довжині (рис. 10.6, крива 1).
В реальній лінії з втратами амплітуди високочастотної напруги та струму дещо зменшуються при поширенні біжучої хвилі від генератора до навантаження (рис. 10.6, крива 2). Амплітуди струмів та напруг на початку і в кінці лінії зв’язані залежностями:
, 
. (10.8)
У даному виразі a - коефіцієнт згасання (затухання) хвилі у фідері, який виражається в неперах на одиницю довжини фідера (1 Нп = 8,7 дБ). Потужності радіосигналу на вході і виході лінії можна представити:
, 
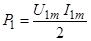. (10.9)
Звідcи коефіцієнт корисної дії фідера, що працює в режимі біжучої хвилі, становить:
. (10.10)
Теоретично наближене значення коефіцієнта згасання можна знайти за формулою:
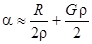. (10.11)
Тут R - питомий опір провідників лінії, а G - питома провідність ізоляції між провідниками лінії.
Для двопровідної повітряної лінії другий доданок у виразі (10.11) можна вважати таким, що дорівнює нулю. Питомий опір провідників лінії, з врахуванням скін-ефекту, визначається:
. (10.12)
Тут r - радіус провідників (мм), m - відносна магнітна проникність провідників лінії, s - електропровідність матеріалу провідників (См/м), l - довжина електромагнітної хвилі (м).
Точний розрахунок коефіцієнта згасання a для різних ліній досить складний. Цей параметр, як один з найважливіших, надається виробниками фідерів. Параметри деяких коаксіальних фідерів для режиму біжучої хвилі наведені в таблиці 10.1.
Таблиця 10.1
| Марка | r, Ом | k | a, дБ/м на f=50 МГц | U роб., кВ |
| РК – 75 – 4 – 15 | 1.5 | 0.08 | 2.5 | |
| РК – 50 – 9 – 12 | 1.5 | 0.05 | 5.0 | |
| RG – 58 / U | 1.5 | 0.1 | - | |
| RG – 213 / U | 1.5 | 0.05 | - |
Якщо антена не узгоджена з фідером за опором (r ¹ RА, XА ¹ 0), то останній працює в режимі змішаних хвиль. Режим змішаних хвиль характеризується коефіцієнтом стоячої хвилі (КСХ). Стояча хвиля (рис. 10.6, крива 3) утворюється при взаємодії падаючої та відбитої від навантаження (антени) хвиль. Максимуми напруги стоячої хвилі (Umax = Uпад + Uвід) утворюються в тих перетинах лінії, де фази падаючої і відбитої хвилі збігаються, в той час як мінімуми (Umin = Uпад - Uвід) - в тих перетинах, де фази протилежні. Важливо пам’ятати, що довжина стоячої хвилі в лінії вдвічі менша від довжини падаючої та відбитої хвиль.
Величина КСХ, за визначенням, дорівнює відношенню максимального та мінімального значень напруги стоячої хвилі у відповідних перетинах лінії:
. (10.13)
Часом використовується інша характеристика режиму змішаних хвиль - коефіцієнт біжучої хвилі (КБХ). Це величина, обернена до КСХ:
. (10.14)
Якщо антена резонує на робочій частоті (XА = 0), а хвильовий опір фідера не збігається з активним опором антени, то:
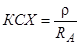при 
; 
при 
. (10.15)
За умови ідеального узгодженні фідера з антеною КСХ=КБХ=1. При сильному неузгодженні КСХ прямує до ¥, а КБХ – до 0.
На практиці для визначення КСХ не обов’язково будувати графік стоячої хвилі в лінії (профіль лінії), якщо є технічна можливість виміряти окремо амплітуди падаючої та відбитої хвиль:
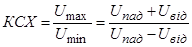. (10.16)
На такому принципі грунтується робота більшості приладів для вимірювання коефіцієнта стоячої хвилі у фідерах - КСХ-метрів.
Якщо чисельник і знаменник правої частини останнього виразу розділити на Uпад і врахувати, що Uвід / Uпад = p, де p-коефіцієнт відбивання хвилі від навантаження, то:
. (10.17)
У режимі змішаних хвиль коефіцієнт корисної дії фідера знижується в порівнянні зі значенням, яке дається формулою (10.10) для режиму біжучої хвилі. Це пояснюється додатковими втратами енергії на нагрівання провідників у пучностях струму та діелектричними втратами в ізоляторах у пучностях напруги. В радіотехнічній літературі наводиться наступна залежність:
. (10.18)
Формула справедлива і для режиму біжучої хвилі, якщо вважати КСХ=1:
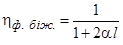. (10.19)
Для малих значень коефіцієнта згасання a:
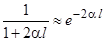. (10.20)
У такому випадку вирази (10.19) та (10.10) дають близькі значення коефіцієнта корисної дії фідера.
За формулою (10.18) можна побудувати сімейство графіків hф=f(КСХ) для різних значень початкових коефіцієнтів корисної дії фідера, коли КСХ=1 (рис. 10.7).
Аналіз графіків дозволяє зробити такі висновки: при малих початкових втратах (малий коефіцієнт згасання a та мала довжина фідера l) припустимою є робота фідера з КСХ величиною до 3-5 одиниць; при значних початкових втратах,
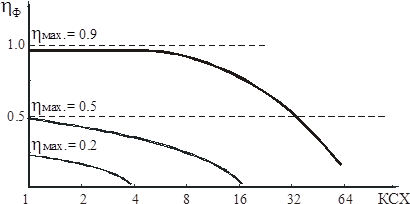
Рис. 10.7
внаслідок низької якості фідера (великі значення a чи l), додаткові втрати від стоячих хвиль теж зростають, і припустимим слід вважати КСХ £ 2.
