Электр тогы, ток күші. Егер өткізгіште электр өрісін тудыратын болсақ, онда оның еркін зарядтары реттелген қозғалыста болады. Өрістің кернеулігінің бағытымен оның оң зарядтары, кернеуліктің бағытына қарама - қарсы бағытта теріс зарядтары қозғалады. Сөйтіп өткізгіштің бойында ток жүреді (2.1-сурет).
2.1-сурет
Олай болса, ток деп зарядталған бөлшектердің бағытталған қозғалысын айтамыз. Өткізгіштегі токтың бағытына оң зарядтың бағытын аламыз. Ток өткізгіштің ұштарындағы потенциалдар айырымы теңескенше жүреді.
Электр тогын мөлшері жағынан сипаттау үшін ток күші уақыт бірлігі ішінде өткізгіштің бір өлшем көлденең қимасынан өтетін зарядтың шамасына тең.
(2.1)
Егер токтың күші мен бағыты уақыт аралығында өзгермейтін болса, онда ондай токты тұрақты ток дейміз.
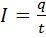(2.2)
мұнда q - өткізгіштің көлденең қимасынан t уақыт ішінде өтетін зарядтың шамасы.
Ток күшінің өлшем бірлігі: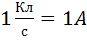 
(Ампер)
Токты ток күшімен қатар, токтың тығыздығы деген шамамен сипаттаймыз. Ток тығыздығы векторлық шама:
(2.3)
Өлшем бірлігі: 
Егер өткізгіштегі заряд тасушылар саны n және оның әрқайсысының заряды е болса, онда бірлік dt уақыт ішінде өткізгіштің S қимасынан өтетін зарядтар шамасы:
Ток күші:
(2.4)
Ток тығыздығы:
(2.5)
Егер ток кез келген тұйық контур арқылы өтсе, онда векторлық ағын ретінде қарастырамыз:
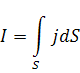
Электр қозғаушы күш. Өткізгіште ток тұрақты болу үшін өткізгіштің ұштарындағы потенциалдар айырымы (кернеуі) тұрақты болуы керек. Өткізгіштің ұштарында тұрақты кернеу болу үшін белгілі бір энергия қоры болуы керек. Ондай энергия көзі ток көздері болады. (батарея, динамомашин т.б). Ток көздерінде энергияның басқа түрі электр энергиясына айналады. Мысалы, динамомашинада механикалық энергия, Гальвани элементі мен аккумуляторда химиялық реакция кезінде бөлінетін энергия электр энергиясына айналады. Сондықтан ток көзінің күшін бөгде күштер деп атайды. Сөйтіп, осындай бөгде күштер арқылы тізбекте токты тұрақты ұстап тұрады. Зарядтарды тасымалдау жұмысын жасайтын бөгде күштерді әдетте электр қозғаушы күштер дейді:
(2.6)
Өлшем бірлігі: 
.
Енді ұзындығы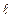 
өткізгішті ток көзіне қоссақ, оның бойынан ток жүреді де де, ұштарында потенциалдар айырымы (кернеу) пайда болады. Ток потенциалдың кему жағына бағытталған. Өткізгіштің 
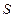–көлденең қимасынан заряд өтіп орын ауыстырғанда істелетін жұмыс:
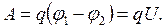
(2.7)
Сөйтіп өткізгіштің ұштарындағы потенциалдар айырымы:
q зарядына әсер ететін бөгде күш:
,
мұндағы 
- бөгде күштің өріс кернеулігі. Тұйық тізбек бойындағы зарядқа әсер етуші бөгде күштердің жұмысы:
(2.8)
.
Зарядқа бөгде күштерден басқа электростатикалық өріс күші 
әсер етеді. Сонда
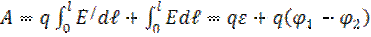(2.9)
Тұйық тізбек үшін электростатикалық күштің шамасы нольге тең, бұл жағдайда жұмыс:
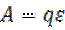(2.10)
Ом заңдары. Өткізгіштің кедергісі. Неміс физигі Г. Ом тәжрибелер жасау арқылы мынадай қортындыға келген: тұрақты температурада өткізгіштегі ток күші оның ұштарындағы кернеуге тура пропорционал да, кедергісіне кері пропорционал болады.
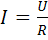(2.11)
Мұнда I=1A, U=1B, R=1Ом, 
, G - электр өткізгіштік. Кедергінің кері шамасы, яғни электрөткізгіштік сименспен (См) өлшенеді. Өткізгіштердің кедергісі оның ұзындығына тура пропорционал да, көлденең қимасына кері пропорционал:
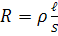(2.12)
- өткізгіштің ұзындығы, S – көлденең қимасының ауданы,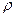 
- өткізгіштің меншікті кедергісі.
Меншікті кедергінің кері шамасы меншікті өткізгіштік деп аталады:
γ = 
(2.12/)
мұның өлшем бірлігі: См/м.
Ом заңының дифференциал түрін жазайық:
(2.13)
(2.13) формула Ом заңының дифференциал түрі.
Өткізгіштің кедергісі температурасына байланысты, температурасы артса кедергісі артады, температурасы төмендесе кедергісі азаяды.
R0 - 00C температурасындағы кедергі, Rt - t температурадағы кедергі.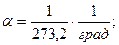 
Кейбір заттардың төменгі температурада кедергісі күрт төмендеп, нольге жуықтайды. Осы құбылыс асқан өткізгіштік деп аталады.
Тұйық тізбекке арналған Ом заңы: тұйық тізбектегі ток күші ЭҚК шамасына тура пропорционал да, тізбектің сыртқы және ішкі кедергілерінің қосындысына кері пропорционал болады:
(2.14)
мұндағы r – ішкі кедергі.
Өткізгіштерді тізбекке қосудың екі түрі бар: егер өткізгіштерді тізбектей қоссақ (2.2,а-сурет), онда олардың толық кедергісі:
(2.15)
Тізбектей жалғанған бірнеше өткізгіштен тұратын тізбектің кедергісі жеке өткізгіштер кедергілерінің қосындысына тең.
Өткізгіштерді тізбектей жалғағанда ток күштері тең, ал тізбектегі жалпы кернеу оның бөліктеріндегі кернеулердің қосындысына тең болады, ал жалпы кедергі әрбір өткізгіштің кедергілерінің қосындысынан тұрады:
Өткізгіштерді параллель қоссақ (2.2,б-сурет), онда олардың толық кедергісі:
(2.16)
Параллель жалғанған бірнеше өткізгіштен тұратын тізбектің кедергісінің кері шамасы жеке өткізгіштер кедергілерінің кері шамаларының қосындысына тең.
Өткізгіштерді параллель жалғағанда, тізбектің барлық бөліктерінде кернеу бірдей, ал жалпы ток күші әрбір өткізгіштегі ток күштерінің қосындысына тең, жалпы кедергі әрбір өткізгіштің кедергісінен кем болады.
а) б)
(2.2-сурет),
Тұрақты токтың қуаты және жұмысы. Джоуль-Ленц заңдары. Кернеуі U болатын өткізгіш арқылы ток жүргенде өткізгіш қызып, жылу бөлініп шығады. Осы жылудың бөлініп шығуы, зарядтарды тасымалдаушы электр күштерінің жұмысына байланысты:
Өткізгіштің көлденең қимасынан dt уақыт ішінде q заряд ағын өтеді десек, сонда электр тоғының істейтін жұмысы:
Энергияның сақталу заңы бойынша бұл жұмыс өткізгіште бөлініп шығатын жылуға тең болады:
; 
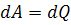(2.17)
(2.17) өрнекті Джоуль -Ленц заңы дейді.
Көлемі 
болатын цилиндр формалы өткізгіш алсақ, Джоуль-Ленц заңы бойынша онда бөлінетін жылу мөлшері:
мұндағы, 
Уақыт бірлігі ішінде көлем бірлігінде бөлінетін жылуды
жылудың меншікті қуаты дейді. Ол
;
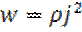(2.18)
(2.18) формула Джоуль – Ленц заңының дифференциалдық формасы.
Токтың қуаты:
(2.19)
Өлшем бірлігі: 
Кирхгофф ережелері. Тармақталған электрлік тізбектерді есептегенде түйін, тармақ, контур деген түсініктер еңгізіледі.
Электр тізбегінің тармағы, тізбектеп қосылған ЭҚК энергия көздерінен және қабылдағыштардан (кедергілерден) тұратын бөлігі.
Тізбектің түйіні – үш немесе одан да көп тармақтардың қосылу жері.
Тізбектің контуры – бірнеше тармақтардан құрылған тізбектің тұйық бөлігі.
Тізбекте үштен кем емес өткізгіштер түйісетін нүктені түйіндер (2.3-сурет) дейді.
Кирхгоффтың бірінші ережесі: Түйінде тоғысатын токтардың алгебралық қосындысы нольге тең болады.
2.3сурет
Жалпы түрде:
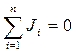(2.20)
Бұл ережені былайша түсіну керек. Егер түйіндегі токтардың алгебралық қосындысы нольден өзгеше болса, түйінде зарядтар көбейіп, не азайып кетер еді де, бұл тізбектегі токтың өзгеруіне әкеліп соғады. Кирхгофтың бірінші заңы электрлік сызбаның тармақтарына қолданылады. (2.12) теңдеуіндегі токтардың бірдей таңбалары, қарастырылып жатқан түйін бойынша бірдей оң бағытқа ие токтарға алынады. Есептеу кезінде токтардың оң бағыттары ерікті алынады
2. Кирхгоффтың екінші ережесі Ом заңын тізбектердің бөліктері үшін жазудан шығады. Кирхгофтың 2-ші заңы тізбектің контурларына қолданылады, 2.4-сурет.
|
2.4-сурет
Контурды айналуды өз қалауымызша аламыз. Контурды айналу бағытымен токтың бағыты бірдей болса, ток оң таңба мен ал қарсы болса, теріс таңбамен алынады. Контурды айналу бағытында ток көзінің оң полюсінен теріс полюсінен ауысқанда 
теріс таңбамен, ал оң полюсіне өтсе оң таңбамен алынады.
Жалпы түрде:
(2.21)
Сонымен, Кирхгофтың екінші ережесі: кез келген тұйық контур үшін э.қ.к-нің алгебралық қосындысы ток күшінің кедергіге көбейтіндісінің алгебралық қосындысына тең.
Магнит өрісі
Магнит өріісі және оның сипаттамалары.
Электр зарядын қоршаған ортада электростатикалық өріс болатыны сияқты, токтарды қоршаған ортада магнит өрісі болады. Магнит өрісі осы өріске әкелінген тогы бар өткізгішке әсер ететін күш арқылы білінеді. Ток айналасында магнит өрісі болатынын бірінші рет 1820 жылы дат физигі Эрстед тәжірибе жүзінде ашқан. Ол тогы бар өткізгіш маңында магнит стрелкасын қойсақ (3.1-сурет), стрелканың ток бағытына қарай бұрылатынын байқаған. Магнит өрісін зерттеу үшін тогы бар жазық тұйықталған контур (3.2-сурет)қолданылады.
Рамка арқылы ток жүргенде, ол белгілі бір бұрышқа бұрылады. Рамканың айналу бағыты арқылы магнит өрісінің бағыты анықталады. Магнит өрісінің рамканы айналдырушы моменті
(3.1)
мұндағы 
тогы бар рамканың магнит моменті векторы. 
магнит индукция векторы, 
контурғы нормалы бірлік вектор, 
магнит өрісінің токқа әсер ететін күшін сипаттайды.
3.1-сурет 3.2-сурет
Олай болса, магнит индукциясы айналу моментіне пропорционал шама:
(3.2)
Магнит өрісі магнит индукциясының күш сызықтарымен кескінделеді. Ол сызықтар тұйық болады және кез келген нүктесі арқылы жүргізілген жанама индукция векторымен бағыттас болады. Магнит индукция векторының бағытын бұранда ережесі бойынша да анықтауға болады. Өлшем бірлігі тесла (Тл).
Ампердің болжамына қарағанда кез келген денелердің атомдары мен молекулаларының қозғалысынан пайда болатын микротоктар болады. Микротоктар денелер ішінде өзінің магнит өрісін тудырып макротоктардың бағытын өзгертуі мүмкін. Макроток деп өткізгіш бойымен өтіп жататын токты айтады. Сондықтан индукция векторы 
микротоктар мен макротоктардың біріккен өрісін сипаттайтын векторлық шама. Макротоктар туғызатын магнит өрісі кернеулік векторы деп аталатын 
шамамен сипатталады. Біртекті ортада
(3.3)
Мұнда 
- магнит тұрақтысы, 
ортаның магниттік өтімділігі, яғни сыртқы макротоктардың магнит өрісінің ортаның микротоктарының өрісінің әсерінен қанша есе өсетіндігін көрсетеді.
Француз физиктері Био және Савар тәжірибелер арқылы әртүрлі пішінді тұрақты токтың айналасындағы магнит өрістерін зерттеген. Лаплас сол зерттеулердің нәтижелерін жинақтап кез келген пішіндегі контурдың бөліктеріне жарамды магнит өрісінің қорытқы индукциясын анықтауға болатын заңдылықты ашты. Ол заңдылық бойынша I тогы бар өткізгіштің 
элементінің өрістің бір А нүктесіндегі магнит индукциясы:
,
модулы 
(3.4)
Осы өрнек, электромагниттік құбылыстар үшін Био-Савар- Лаплас заңы деп аталады.
3.3-сурет
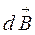векторы және 
құрайтын жазықтыққа перпендикуляр болып, индукция сызықтарына жанама болады (3.3-сурет), бағыты бұранда ережесі бойынша анықталады.
Суперпозиция принципін қолданып, барлық ток элементтерінің магнит индукциясы векторларының қосындыларын интегралдау арқылы анықтауға болады
. (3.5) Био-Савар-Лаплас заңының (3.4 өрнектің) кейбір симметриялы токтардың магнит өрісін есептеу үшін қолданылуы:
1. Шексіз түзу өткізгіштің бойымен өткен токтың магнит өрісін анықтау. Өрістің 
нүктесіндегі магнит индукциясын есептейік. Өрістің нүктесіндегі элементінің 
индукцияларының бағыттары бірдей (чертеж жазықтығына перпендикуляр) болады. 3.4-суреттен мына қатынастарды жазуға болады:
,
Био-Савар-Лаплас заңы бойынша:
 |
3.4-сурет
Бұрыш 
шексіз тұзу өткізгіштің барлық элементтері үшін 00-ден 1800 дейін өзгереді деп интегралды есептейік:
(3.6)
2. Дөңгелек токтың центріндегі магнит өрісін анықтау. Мұндай өткізгіштің барлық элементтері О центрінен бірдей R қашықтықта болады, (3.5-сурет). Магнит индукциясының бағыты центр арқылы контурға перпендикуляр бағытталады. Сондықтан (3.4) өрнекке сәйкес
3.5-сурет
,
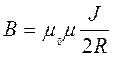(3.7)
3.Ұзын соленоид немесе катушка ішіндегі магнит индукциясы тең:
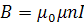(3.8)
мұндағы n -соленоидтың 1м ұзындығына келетін орам саны.
соленоид ішіндегі өріс:
(3.8/)
Соленоид - 3.6, а -суретте көрсетілгендей, жалпы өзекшеге біртекті оратылған саны өте көп орамнан тұратын цилиндр катушка.
Тороид – тора (тәурат) пішінді өзекшеге (3.6, б -сурет) оратылған орамдардан тұратын дөңгелек катушка. Магнит өрісі:
(3.9)
a) б)
3.6 -сурет
Тогы бар өткізгішке магнит өрісінің әсер күшін Ампер зерттеп анықтады. Ампер заңы: магнит өрісіндегі тогы бар өткізгішке, магнит өрісі тарапынан әсер ететін күш өткізгіштегі ток күшіне, өткізгіштің ұзындығына және магнит индукциясының көбейтіндісіне тура пропорционал:
Ампер күшінің модулі:
(3.10)
Мұндағы ток бағытымен индукция векторының арасындағы бұрыш.
а) б)
3.7-сурет
Ампер күшінің бағыты сол қол ережесі бойынша анықталады (3.7, а -сурет). Ампер күшінің бағытын сол қол ережесі бойынша анықтауға болады, яғни саусақтар ток бағытын көрсетіп, магнит индукциясының векторы алақанды тесіп өтетеін болса, онда бас бармақ Ампер күшінің бағытын көрсетеді. Магнит индукциясының бағыты бұранда ережесі бойынша анықталады (3.7, б -сурет), яғни ток бағыты бұранданың оң бағытталған ілгерілемелі қозғалысын көрсетсе, онда оның айналмалы сабының бағыты индукция сызығының бағытын көрсетеді.
Параллель токтардың өзара әсерлесуі.
Өзара әсерлесу күштерін анықтау үшін бір - бірінен R ара қашықтықта орналасқан шексіз ұзын, түзу параллель
а) б)
3.8-сурет
өткізгіштерде I1 және I2 токтары болсын. Бұлардың әрқайсысы өз маңында магнит өрісін тудырады да, 3.8-суреттегідей, олар Ампер заңы бойынша бір бірімен әсер етеді. I1 тогы бар өткізгіштің магнит өрісіне I2 тогы бар өткізгішті орналастырсақ, онда I1 токтың магнит өрісінің күштері I2 токтың d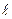 
элементіне әсер етеді. Ампер заңына сәйкес I1 ток тарапынан dF12, ал I2 ток тарапынан dF21 күштері бір-біріне әсер етеді.
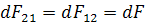
Олай болса, екі токтың арасындағы өзара әсер күші:
(3.11)
Бағыттас параллель токтар (3.8, а -сурет) бір-біріне тартылады, қарама-қарсы токтар (3.8, б –сурет) бір-бірінен тебіледі. Ток күшінің өлшем бірлігі ампер (А) деп вакуумда бір-бірінен 1м қашықтықта орналасқан шексіз ұзын параллель екі өткізгіштен ток өткенде олардың арасында әрбір метр ұзындыққа 2·10-7 Н -ға тең күш әсерін туғызатын ток күшін айтады. Осыдан тұрақты 
дің мәні табылады:
.
Лоренц күші. Магнит өрісінің қозғалыстағы зарядқа тигізетін әсері.
Магнит өрісі тек тогы бар өткізгішке ғана емес, кез келген қозғалыстағы зарядтарға да әсер ететіндігін көптеген эксперименттердің нәтижелері дәлелдейді. Магнит өрісіндегі әр зарядқа әсер ететін күшті Лоренц күші (Fл) деп атайды. Ол мынаған тең
(3.12)
- жылдамдығы, - сол өрістің индукция векторы. Лоренц күшінің бағытын сол қол ережесі бойынша анықтайды, яғни 3.9-суреттегідей магнит индукциясы алақанды тесіп өтсе, саусақтар электрондар жылдамдығының бағытын көрсетсе, онда бас бармақ Лоренц күшінің бағытын анықтайды.
Лоренц күшінің модулі
(3.13)
- 
жылдамдық пен 
индукция векторы арасындағы бұрыш. Лоренц күші әрқашанда зарядталған бөлшектің қозғалыс жылдамдығына перпендикуляр болады, сондықтан ол қозғалыстың бағытын ғана өзгертіп, жылдамдық модулін өзгертпейді.
3.9-сурет
Олай болса Лоренц күші жұмыс жасамайды, зарядталған бөлшектердің кинетикалық энергиясы өзгермейді. Егер қозғалыстағы зарядқа магнит өрісімен қатар электр өрісі де әсер ететін болса, онда қорытқы күш
(3.14)
Бұл өрнек Лоренц формуласы деп аталады.
3.10-суретте 
, 
(суретте нүктелермен белгіленген өріс бізге қарай бағытталған), және 
векторларыының оң заряд үшін өзара бағытталулары көрсетілген. Осы магнит өрісінде, сол бағытта қозғалып бара жатқан теріс зарядқа Лоренц күші қарама қарсы бағытта әсер етеді.
Зарядталған бөлшектердің біртекті магнит өрісіндегі қозғалысын қарастырайық:
1. Зарядталған бөлшектің қозғалыс жылдамдығы магнит индукциясының күш сызықтарының бойымен бағытталса, онда 
немесе 
, (3.13) формула бойынша Лоренц күші нолге тең болады да, магнит өрісі бөлшекке әсер етпейді, ол бірқалыпты түзу сызықты қозғалады.
2.Зарядталған бөлшектің қозғалыс жылдамдығы , өріс индукция векторына перпендикуляр бағытталса, Лоренц күші модулі тұрақты болып, бөлшек траекториясына нормаль бағытталады және жылдамдық бағытын өзгертеді. Бөлшек шеңбер бойымен қозғалады, оның радиусы мына қатынастан табылады:
осыдан
(3.15)
3.10-сурет
Бөлшектің айналыс периоды:
Осы өрнекке (3.15) формуласын қойсақ, период:
(3.16)
3.Зарядталған бөлшектің қозғалыс жылдамдығы , индукция векторымен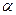 
бұрыш жасай бағытталса, онда бөлшектің қозғалу траекториясы спираль тәрізді (3.11-сурет) болады. Оны екі қозғалыстың нәтижесі деп қарастырсақ:
1) 
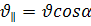жылдамдықпен өріс бойымен түзу сызықты бірқалыпты қозғалады
2) 
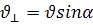жылдамдықпен өріске перпендикуляр жазықтықта бір қалыпты шеңбер бойымен қозғалады. Шеңбердің радиусы (3.13) өрнекпен анықталады. Екі қозғалысты қосудың нәтижесінде осі магнит өрісіне параллель спираль бойымен қозғалыс пайда болады. Бұранда сызықтың қадамы:
Осы өрнекке (3.14) формуланы қоямыз:
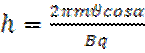(3.17)
өлшем бірлігі: м(метр).
3.11-сурет
Зарядталған бөлшектердің үдеткіштері деп электр және магнит өрістерінің әсерімен жоғары энергиялы зарядталған бөлшектер (электрон, протон, мезон және т.б.) шоғы алынатын және олардың қозғалысы басқарылатын қондырғыларды айтады. Олардың қатарына: сызықты үдеткіш, сызықты резонансты үдеткіш, циклотрон, фазотрон, синхротрон, синхрофазотрон, бетатрон жатады.
Магниттік индукция векторының ағыны. Остроградский-Гаусс теоремасы.
Магнит өрісінде индукция векторы 
шамасы жағынан барлық жерде бірдей және бағыттас болса, мұндай өрісті біртекті магнит өрісі деп атайды. Біртекті өрістің индукция векторының күш сызықтары параллель болады. Осындай біртекті өрісте ауданы S бет перпендикуляр болып орналассын. Сонда магниттік векторының жазық беттің ауданына S көбейтіндісі осы бет арқылы өтетін магнит ағыны деп аталады.
Егер жазық бетке жүргізілген нормаль 
индукция векторымен бұрыш жасай орналасса
(3.18)
бұрышының мәніне сәйкес 
болуы мүмкін. Кез келген S бет арқылы өтетін магнит ағыны мына түрде жазылады
, 
Кез келген тұйық бет арқылы өтетін магнит ағыны әр уақытта нолге тең болады:
(3.19)
Осы формула магнит өрісі үшін Остроградский-Гаусс теоремасы деп аталады. Магнит ағынының өлшем бірлігі Вебер (Вб). 1Вб=1Тл/м2. Бұл теореманың физикалық мәні, табиғатта (электр зарядтар сияқты) магнит индукциясының күш сызықтарының бір жерден басталып, екінші жерде аяқтала алатындай магниттік зарядтардың болмайтындығын көрсетеді
Магнит өрісіндегі тұйық контурдың индукция векторының циркуляциясы деп мынадай интегралды айтамыз:
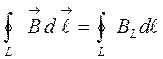(3.20)
Магнит өрісінің индукция векторының циркуляциясы нөлге тең болмайды. Мұндай өрістерді құйынды өріс деп атайды.
Вакуумдағы магнит өрісі үшін толық ток заңы: Кез келген тұйық контур арқылы өтетін магнит индукция векторының циркуляциясы магнит тұрақтысын контур арқылы өтетін токтардың алгебралық қосындысына көбейткенге тең, яғни
(3.21)
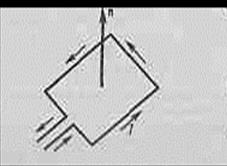
мұнда n -еркін формалы L контур арқылы өтетін ток саны. Әрбір ток қанша рет контурмен қамтылғанына байланысты есептелінеді. Ток оң болады, егер контурды айналып өту бағыты оң бұрғы ережесімен
байланысты болса; кері бағыттағы ток теріс деп есептеледі. Мысалы, 3.12-суретте бейнеленген токтар жүйесін қарастыруға болады.
3.12-сурет
(3.22)
Магнит өрісінде тогы бар өткізгіш және контур орын ауыстырғанда істелетін жұмыс. Сыртқы біртекті магнит өрісінде тогы бар өткізгіш еркін қозғалатын болсын. Магнит өрісінде тогы бар өткізгіш қозғалып орын ауыстырғанда ампер күшінің әсерінен жұмыс істелінеді. Егер 3.13, а -суретте көрсетілгендей контурдың бір қабырғасы түзу өткізгіш ретінде қозғалатын болса, онда сол ұзындығы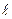 
түзу өткізгіштің бойымен ток өткенде өткізгіш қозғалып, орын ауыстырады делік. Магнит өрісі контур жазықтығына перпендикуляр. Ток күші мен индукция векторының арасындағы бұрыш 900. Сонда Ампер заңы бойынша күш 
, бағыты сол қол ережесімен анықталады. Осы күштің әсерінен өткізгіш dx арақашықтыққа орын ауыстырған кездегі магнит өрісінің жұмысы:
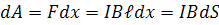
мұндағы 
- өткізгіштің жүріп өткен магнит өрісінің ауданы, 
екенін ескерсек,
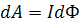(3.23)
Сонымен, магнит өрісінде тогы бар өткізгіш орын ауыстырғанда істелетін жұмыс ток күші мен S ауданы арқылы өтетін магнит ағынының көбейтіндісіне тең болады. 
- қозғалыстағы өткізгіш қиып өткен магнит ағыны.
а) б)
3.13-сурет
Магнит өрісінде тогы бар тұйық контур 3.13, б -суреттегідей қозғалады делік. Бұл жағдайда да Ампер күші әсерінен жұмыс істелінеді, ол мынаған тең
(3.24)
мұндағы 
; 
- контур жазықтығын бірінші күйінде, 
- екінші күйінде тесіп өтіп тұрған магнит ағындары. Тогы бар тұйық контур магнит өрісінде орын ауыстырған кезде істелетін жұмыс ток күші мен контур жазықтығынан өтіп тұрған магнит ағындарының айырмасына көбейткенге тең. Осы (3.24) теңдеуі әр түрлі пішінді тұйық контур үшін және біртекті емес магнит өрістері үшін қолданылады.
