В задачах 1 – 20 известно, что проведено n равноточных измерений некоторой физической величины и найдено среднее арифметическое результатов измерений` х. Все измерения проведены одним и тем же прибором с известным средним квадратическим отклонением ошибок измерений. Считая результаты измерений нормально распределенной случайной величиной, найти с надежностью g доверительный интервал для оценки истинного значения измеряемой физической величины.
1. ` х = 40,2; s = 2,3; g = 0,90; n = 16.
2. ` х = 83,1; s = 3,2; g = 0,95; n = 24.
3. ` х = 45,7; s = 3,7; g = 0,93; n = 9.
4. ` х = 48,9; s = 4,1; g = 0,85; n = 15.
5. ` х = 20,3; s = 1,8; g = 0,95; n = 18.
6. ` х = 73,2; s = 5,7; g = 0,92; n = 25.
7. ` х = 88,3; s = 6,1; g = 0,95; n = 30.
8. ` х = 68,1; s = 5,1; g = 0,90; n = 17.
9. ` х = 72,8; s = 4,7; g = 0,92; n = 14.
10. ` х = 83,7; s = 6,2; g = 0,90; n = 12.
11. ` х = 47,2; s = 3,4; g = 0,95; n = 28.
12. ` х = 53,1; s = 4,2; g = 0,85; n = 8.
13. ` х = 37,8; s = 6,7; g = 0,80; n = 30.
14. ` х = 41,7; s = 3,4; g = 0,95; n = 12.
15. ` х = 87,4; s = 7,1; g = 0,90; n = 14.
16. ` х = 91,2; s = 6,8; g = 0,85; n = 17.
17. ` х = 48,5; s = 4,2; g = 0,95; n = 18.
18. ` х = 71,7; s = 5,3; g = 0,90; n = 14.
19. ` х = 82,5; s = 3,4; g = 0,90; n = 20.
20.` х = 34,2; s = 2,8; g = 0,95; n = 22.
В задачах 21 – 40 задана выборка значений нормально распределенного признака Х (даны значения признака хi и соответствующие им частоты ni). Найти: а) выборочную среднюю`х и исправленное среднее квадратическое отклонение s; б) доверительный интервал, покрывающий неизвестное математическое ожидание а признака Х; в) доверительный интервал, покрывающий неизвестное среднее квадратическое отклонение s признака Х (надежность оценки во всех вариантах считать равной g=0,95)
21. хi -3 1 2 4 5 7
ni 1 2 2 3 2 4
22. хi -5 -2 3 4 6 7
ni 2 3 1 3 4 5
23. хi -3 -2 1 2 4 6
ni 3 2 2 4 5 1
хi -5 -4 2 4 7 8
24.
ni 1 2 4 5 4 3
25. хi -6 -4 -3 2 3 5
ni 2 4 6 1 3 5
26. хi -2 -1 1 3 5 6
ni 1 2 4 6 3 1
27. хi -7 -6 -4 2 3 5
ni 1 3 5 3 4 2
28. хi -3 -2 1 4 5 7
ni 2 4 6 1 3 3
29. хi -5 -2 -1 2 4 6
ni 1 4 6 5 1 3
30. хi -6 -2 -1 3 5 7
ni 1 2 4 4 5 1
31. хi -3 1 4 5 7 8
ni 4 2 3 5 1 1
32. хi -3 -2 1 3 4 7
ni 1 4 4 3 5 1
33. хi -3 -1 3 4 5 6
ni 2 4 5 4 3 2
34. хi -5 -4 1 3 6 8
ni 2 3 3 4 3 1
35. хi 2 4 5 7 8 9
ni 1 4 3 3 4 1
36. хi -2 -1 1 3 5 6
ni 2 2 3 1 4 5
37. хi -1 2 3 5 7 9
ni 2 3 5 5 1 1
38. хi -5 -4 6 7 8 9
ni 3 3 1 4 2 2
39. хi -4 -2 -1 3 5 6
ni 1 5 5 4 3 1
40. хi -4 -2 -1 2 3 7
ni 1 4 4 3 1 2
41.С целью определения рациональной структуры размерного ассортимента детской одежды проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине обхвата груди Х:
| Обхват груди Х(см) | 54-58 | 58-62 | 62-66 | 66-70 | 70-74 | 74-78 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака.
42. С целью определения рациональной структуры размерного ассортимента детской обуви проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине длины стопы Х:
| Длина стопы Х(мм) | 170-175 | 175-180 | 180-185 | 185-190 | 195-200 | 200-205 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака.
43. С целью определения рациональной структуры размерного ассортимента детской одежды проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине обхвата груди Х:
| Обхват груди Х(см) | 62-66 | 66-70 | 70-74 | 74-78 | 78-82 | 82-86 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака.
44. С целью определения рациональной структуры размерного ассортимента детской одежды проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине обхвата груди Х:
| Обхват груди Х(см) | 62-66 | 66-70 | 70-74 | 74-78 | 78-82 | 82-86 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака.
45. С целью определения рациональной структуры размерного ассортимента детской обуви проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине длины стопы Х:
| Длина стопы Х(мм) | 170-175 | 175-180 | 180-185 | 185-190 | 195-200 | 200-205 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака.
46.С целью определения рациональной структуры размерного ассортимента детской одежды проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине обхвата груди Х:
| Обхват груди Х(см) | 58-62 | 62-66 | 66-70 | 70-74 | 74-78 | 78-82 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака.
47.С целью определения рациональной структуры размерного ассортимента детской обуви проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине длины стопы Х:
| Длина стопы Х(мм) | 175-180 | 180-185 | 185-190 | 195-200 | 200-205 | 205-210 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака.
48.С целью определения рациональной структуры размерного ассортимента детской обуви проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине длины стопы Х:
| Длина стопы Х(мм) | 175-180 | 180-185 | 185-190 | 195-200 | 200-205 | 205-210 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации.
49.С целью определения рациональной структуры размерного ассортимента детской одежды проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине обхвата груди Х:
| Обхват груди Х(см) | 54-58 | 58-62 | 62-66 | 66-70 | 70-74 | 74-78 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака;
50. С целью определения рациональной структуры размерного ассортимента детской обуви проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине длины стопы Х:
| Длина стопы Х(мм) | 180-185 | 185-190 | 195-200 | 200-205 | 205-210 | 210-215 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака
51.С целью определения рациональной структуры размерного ассортимента детской одежды проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине обхвата груди Х:
| Обхват груди Х(см) | 54-58 | 58-62 | 62-66 | 66-70 | 70-74 | 74-78 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака
52.С целью определения рациональной структуры размерного ассортимента детской одежды проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине обхвата груди Х:
| Обхват груди Х(см) | 54-58 | 58-62 | 62-66 | 66-70 | 70-74 | 74-78 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака.
53.С целью определения рациональной структуры размерного ассортимента детской обуви проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине длины стопы Х:
| Длина стопы Х(мм) | 170-175 | 175-180 | 180-185 | 185-190 | 195-200 | 200-205 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака.
54.С целью определения рациональной структуры размерного ассортимента детской одежды проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине обхвата груди Х:
| Обхват груди Х(см) | 62-66 | 66-70 | 70-74 | 74-78 | 78-82 | 82-86 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака;
55. С целью определения рациональной структуры размерного ассортимента детской одежды проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине обхвата груди Х:
| Обхват груди Х(см) | 62-66 | 66-70 | 70-74 | 74-78 | 78-82 | 82-86 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака
56. С целью определения рациональной структуры размерного ассортимента детской обуви проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине длины стопы Х:
| Длина стопы Х(мм) | 170-175 | 175-180 | 180-185 | 185-190 | 195-200 | 200-205 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака.
57.С целью определения рациональной структуры размерного ассортимента детской одежды проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине обхвата груди Х:
| Обхват груди Х(см) | 58-62 | 62-66 | 66-70 | 70-74 | 74-78 | 78-82 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака.
58.С целью определения рациональной структуры размерного ассортимента детской обуви проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине длины стопы Х:
| Длина стопы Х(мм) | 175-180 | 180-185 | 185-190 | 195-200 | 200-205 | 205-210 |
| Кол-во детей | 25\8 |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака.
59.С целью определения рациональной структуры размерного ассортимента детской обуви проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине длины стопы Х:
| Длина стопы Х(мм) | 175-180 | 180-185 | 185-190 | 195-200 | 200-205 | 205-210 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации v изучаемого признака.
60.С целью определения рациональной структуры размерного ассортимента детской одежды проведено выборочное обследование определенных половозрастных групп детского населения и получено следующее распределение количества детей по величине обхвата груди Х:
| Обхват груди Х(см) | 62-66 | 66-70 | 70-74 | 74-78 | 78-82 | 82-86 |
| Кол-во детей |
Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака Х; 2) определить выборочное среднее хв, выборочное стандартное отклонение σ в и коэффициент вариации V изучаемого признака.
61.Имеются выборочные данные о дневном сборе хлопка (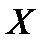
, кг):
| 20-25 | 2-30 | 30-35 | 35-40 | 40-5 |
| Число сборщиков |
Вычислить выборочные среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
62.Имеются выборочные данные о дневном сборе хлопка (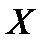, кг):
|
| 20-25 | 2-30 | 30-35 | 35-40 | 40-5 |
| Число сборщиков |
Вычислить выборочные среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
63.Имеются выборочные данные о дневном сборе хлопка (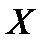, кг):
|
| 20-25 | 2-30 | 30-35 | 35-40 | 40-5 |
| Число сборщиков |
Вычислить выборочные среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
64. Дано распределение расхода сырья, идущего на изготовление одного изделия (, г):
|
| 380-390 | 390-400 | 400-410 | 410-420 | 420-430 |
| Число изделий |
Вычислить выборочные среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
65. Дано распределение расхода материала на изготовление одного изделия:
| Расход материала, см | 240-250 | 250-260 | 260-270 | 270-280 | 280-290 |
| Число изделий |
Вычислить выборочные среднюю; моду, медиану, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
66. Имеются выборочные данные о дневном сборе урожая (, кг):
| |||||
| Число работников |
Вычислить выборочные среднюю, моду, медиану, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
67. Затраты времени на сборку прибора у 70 сборщиков цеха имеют следующее распределение:
| Время, мин | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Число сборщиков |
Вычислить выборочные характеристики этого распределения: среднюю, моду, медиану, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
68.Дано распределение расхода сырья, идущего на изготовление одного изделия (X, г):
|
| |||||
| Число изделий |
Вычислить выборочные среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
69.Группа рабочих изготавливает одинаковую продукцию. Дан ряд распределения рабочих по числу изготавливаемых за смену деталей:
| Число деталей | |||||
| Число рабочих |
Вычислить выборочные среднюю, размах вариации, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
70.Имеются выборочные данные о дневном сборе хлопка (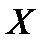, кг):
|
| 20-25 | 2-30 | 30-35 | 35-40 | 40-5 |
| Число сборщиков |
Вычислить выборочные среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
71. Дано распределение расхода сырья, идущего на изготовление одного изделия (, г):
|
| 380-390 | 390-400 | 400-410 | 410-420 | 420-430 |
| Число изделий |
Вычислить выборочные среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
72. Дано распределение расхода материала на изготовление одного изделия:
| Расход материала, см | 240-250 | 250-260 | 260-270 | 270-280 | 280-290 |
| Число изделий |
Вычислить выборочные среднюю; моду, медиану, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
73.Имеются выборочные данные о дневном сборе урожая (, кг):
|
| |||||
| Число работников |
Вычислить выборочные среднюю, моду, медиану, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
74. Затраты времени на сборку прибора у 70 сборщиков цеха имеют следующее распределение:
| Время, мин | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Число сборщиков |
Вычислить выборочные характеристики этого распределения: среднюю, моду, медиану, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
75. Дано распределение расхода сырья, идущего на изготовление одного изделия (X, г):
|
| |||||
| Число изделий |
Вычислить выборочные среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
76. Группа рабочих изготавливает одинаковую продукцию. Дан ряд распределения рабочих по числу изготавливаемых за смену деталей:
| Число деталей | |||||
| Число рабочих |
Вычислить выборочные среднюю, размах вариации, моду, медиану, дисперсию, среднее квадратическое
77.Имеются выборочные данные о дневном сборе хлопка (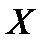, кг):
|
| 20-25 | 2-30 | 30-35 | 35-40 | 40-5 |
| Число сборщиков |
Вычислить выборочные среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
78. Дано распределение расхода материала на изготовление одного изделия:
| Расход материала, см | 240-250 | 250-260 | 260-270 | 270-280 | 280-290 |
| Число изделий |
Вычислить выборочные среднюю; моду, медиану, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
79. Имеются выборочные данные о дневном сборе урожая (, кг):
|
| |||||
| Число работников |
Вычислить выборочные среднюю, моду, медиану, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации
80. Дано распределение расхода сырья, идущего на изготовление одного изделия (, г):
|
| 380-390 | 390-400 | 400-410 | 410-420 | 420-430 |
| Число изделий |
Вычислить выборочные среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
81.В результате специального обследования получено выборочное распределение стажа работников завода (
- стаж работы, лет; 
- эмпирические частоты; 
- теоретические частоты нормального распределения):
|
| |||||||||
|
| |||||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить, согласуется ли гипотеза о нормальном распределении признака X генеральной совокупности с эмпирическим распределением выборки.
82.В результате специального обследования получено выборочное распределение времени простоя фрезерных станков одного цеха ( - время простоя, мин; - эмпирические частоты; - теоретические частоты нормального распределения):
|
| 5,5 | 10,5 | 15,5 | 20,5 | 25,5 | 35,5 | |
|
| |||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить, согласуется ли гипотеза о нормальном распределении признака X генеральной совокупности с эмпирическим распределением выборки
83.В результате обследования получено следующее распределение дневной выручки от продажи продукции в промтоварных магазинах (X - дневная выручка, руб.; - эмпирические частоты (число магазинов); - теоретические частоты, вычисленные в предположении о нормальном законе распределения):
|
| |||||||
|
| |||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить гипотезу о нормальном распределении признака генеральной совокупности.
84.В результате обследования опытных участков одинакового размера получено выборочное распределение урожайности ржи ( - урожайность, ц/га; - эмпирические частоты; - теоретические частоты, вычисленные в предположении о нормальном законе распределения):
|
| |||||||
|
| |||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить, согласуется ли гипотеза о нормальном распределении признака генеральной совокупности с эмпирическим распределением выборки.
85.Установить при уровне значимости 0,05 случайно или значимо: расхождение между эмпирическими и теоретическими частотами, которые вычислены, исходя из предположения, что признак распределен нормально:
|
| ||||||||
|
|
86.В результате специального обследования получено выборочное распределение стажа работников завода ( - стаж работы, лет; - эмпирические частоты; - теоретические частоты нормального распределения):
|
| |||||||||
|
| |||||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить, согласуется ли гипотеза о нормальном распределении признака X генеральной совокупности с эмпирическим распределением выборки.
87.В результате специального обследования получено выборочное распределение стажа работников завода ( - стаж работы, лет; - эмпирические частоты; - теоретические частоты нормального распределения):
|
| |||||||||
|
| |||||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить, согласуется ли гипотеза о нормальном распределении признака X генеральной совокупности с эмпирическим распределением выборки.
88. В результате специального обследования получено выборочное распределение стажа работников завода ( - стаж работы, лет; - эмпирические частоты; - теоретические частоты нормального распределения):
|
| |||||||||
|
| |||||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить, согласуется ли гипотеза о нормальном распределении признака X генеральной совокупности с эмпирическим распределением выборки.
89. В результате специального обследования получено выборочное распределение времени простоя фрезерных станков одного цеха ( - время простоя, мин; - эмпирические частоты; - теоретические частоты нормального распределения):
|
| 5,5 | 10,5 | 15,5 | 20,5 | 25,5 | 35,5 | |
|
| |||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить, согласуется ли гипотеза о нормальном распределении признака X генеральной совокупности с эмпирическим распределением выборки.
90. В результате обследования получено следующее распределение дневной выручки от продажи продукции в промтоварных магазинах (X - дневная выручка, руб.; - эмпирические частоты (число магазинов); - теоретические частоты, вычисленные в предположении о нормальном законе распределения):
|
| |||||||
|
| |||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить гипотезу о нормальном распределении признака генеральной совокупности.
91.Установить при уровне значимости 0,05 случайно или значимо: расхождение между эмпирическими и теоретическими частотами, которые вычислены, исходя из предположения, что признак распределен нормально:
|
| ||||||||
|
|
92. В результате обследования получено выборочное распределение времени, затрачиваемого операторами бухгалтерских машин на обработку документов складского учета (Х- время, с: - эмпирические частоты (количество документов); - теоретические частоты, вычисленные в предположении о нормальном законе распределения):
|
| ||||||
|
| ||||||
|
|
Используя критерий Пирсона, при 
= 0,05 проверить, согласуется ли гипотеза о нормальном распределении признака X генеральной совокупности с эмпирическим распределением выборки.
93. В результате обследования опытных участков одинакового размера получено выборочное распределение урожайности ржи ( - урожайность, ц/га; - эмпирические частоты; - теоретические частоты, вычисленные в предположении о нормальном законе распределения):
|
| |||||||
|
| |||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить, согласуется ли гипотеза о нормальном распределении признака генеральной совокупности с эмпирическим распределением выборки.
94. В результате обследования получено следующее распределение дневной выручки от продажи продукции в промтоварных магазинах (X - дневная выручка, руб.; - эмпирические частоты (число магазинов); - теоретические частоты, вычисленные в предположении о нормальном законе распределения):
|
| |||||||
|
| |||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить гипотезу о нормальном распределении признака генеральной совокупности.
95.В результате специального обследования получено выборочное распределение стажа работников завода ( - стаж работы, лет; - эмпирические частоты; - теоретические частоты нормального распределения):
|
| |||||||||
|
| |||||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить, согласуется ли гипотеза о нормальном распределении признака X генеральной совокупности с эмпирическим распределением выборки.
96.В результате специального обследования получено выборочное распределение времени простоя фрезерных станков одного цеха ( - время простоя, мин; - эмпирические частоты; - теоретические частоты нормального распределения):
|
| 5,5 | 10,5 | 15,5 | 20,5 | 25,5 | 35,5 | |
|
| |||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить, согласуется ли гипотеза о нормальном распределении признака X генеральной совокупности с эмпирическим распределением выборки
97.В результате обследования получено следующее распределение дневной выручки от продажи продукции в промтоварных магазинах (X - дневная выручка, руб.; - эмпирические частоты (число магазинов); - теоретические частоты, вычисленные в предположении о нормальном законе распределения):
|
| |||||||
|
| |||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить гипотезу о нормальном распределении признака генеральной совокупности.
98.В результате обследования опытных участков одинакового размера получено выборочное распределение урожайности ржи ( - урожайность, ц/га; - эмпирические частоты; - теоретические частоты, вычисленные в предположении о нормальном законе распределения):
|
| |||||||
|
| |||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить, согласуется ли гипотеза о нормальном распределении признака генеральной совокупности с эмпирическим распределением выборки.
99.Установить при уровне значимости 0,05 случайно или значимо: расхождение между эмпирическими и теоретическими частотами, которые вычислены, исходя из предположения, что признак распределен нормально:
|
| ||||||||
|
|
100. В результате специального обследования получено выборочное распределение времени простоя фрезерных станков одного цеха ( - время простоя, мин; - эмпирические частоты; - теоретические частоты нормального распределения):
|
| 5,5 | 10,5 | 15,5 | 20,5 | 25,5 | 35,5 | |
|
| |||||||
|
|
101.Имеются следующие данные по группе предприятий о выпуске продукции (X, тыс. шт.) и себестоимости одного изделия (Y, руб.):
|
| 2,0 | 3,5 | 4,0 | 4,5 | 5,5 | 6,0 |
| Y | 1,9 | 1,7 | 1,8 | 1,6 | 1,5 | 1,4 |
Вычислить коэффициент корреляции на основе этих данных. При уровне значимости 0,05 проверить нулевую гипотезу о равенстве нулю коэффициента корреляции в генеральной совокупности. Построить уравнение линейной регрессионной зависимости и объяснить его смысл. Спрогнозировать среднюю себестоимость одного изделия при выпуске 6,5 тыс. шт.
102.Средняя урожайность пшеницы и глубина вспашки по фермерским хозяйствам даны в следующей таблице:
| Глубина вспашки, см | ||||||
| Средняя урожайность | 8,1 | 8,3 | 8,2 | 9,1 | 10,3 | 10,8 |
При 
= 0,05 проверить значимость корреляционной связи глубины вспашки и средней урожайности пшеницы. Если связь значима, составить уравнение регрессии. Объяснить его. Спрогнозировать урожайность пшеницы при глубине вспашки в 11,5 см.
103.Определить тесноту связи общего веса некоторого растения (, г) и веса его семян (Y, г) на основе следующих выборочных данных:
Дата добавления: 2017-02-11; Мы поможем в написании ваших работ!; просмотров: 903 | Нарушение авторских прав Поиск на сайте: Лучшие изречения:  | 2219 -  |
Ген: 0.012 с.