адача 1.
Три стрелка производят по одному выстрелу в цель независимо друг от друга. Вероятность попадания в цель для каждого из них равны соответственно 0,7; 0,8; 0,9. Найти вероятность того, что: а) в цель попадет только один стрелок;
б) в цель попадут только два стрелка; в) в цель попадет хотя бы один стрелок.
ешение.
а) Рассмотрим следующие события:
А1 – первый стрелок попал в цель;
А2 – второй стрелок попал в цель;
А3 – третий стрелок попал в цель;
`А1 – первый стрелок не попал в цель;
`А2 – второй стрелок не попал в цель;
`А3 – третий стрелок не попал в цель.
По условию Р(А1) = 0,7; Р(А2) = 0,8; Р(А3) =0,9; Р(`А1) = 1 – 0,7 = 0,3;
Р(`А2) = 0,2; Р (`А3) = 0,1.
Пусть событие В – попал только один стрелок. Тогда
В=А1`А2`А3+`А1А2`А3+`А1`А2 А3
Отсюда в силу несовместности событий-слагаемых и независимости
событий – сомножителей
Р(В) = Р(А1) Р(`А2) Р(`А3) + Р(`А1) Р(А2) Р(`А3) + Р(`А1) Р(`А2) Р(А3) =
0,7 × 0,2 × 0,1 + 0,3 × 0,8 × 0,1 + 0,3 × 0,2 × 0,9 = 0,092
б) Пусть событие С – попадут только два стрелка. Тогда
С = А1А2`А3 + А1`А2А3 +`А1А2А3.
Отсюда
Р(С) = 0,7 × 0,8 × 0,1 + 0,7 × 0,2 × 0,9 + 0,3 × 0,8 × 0,9 = 0,398
 в) Пусть событие D – попал хотя бы один стрелок. Тогда противоположное событие`D – не попал ни один из них, т.е..
в) Пусть событие D – попал хотя бы один стрелок. Тогда противоположное событие`D – не попал ни один из них, т.е..

Поэтому =0,3 × 0,2 × 0,1 = 0,006.
Отсюда P(D) = 1 – P(D) = 1 – 0,006 = 0,994.
адача 2.
Среди 15 микрокалькуляторов, имеющихся в вычислительной лаборатории, лишь 6 новых, а остальные – бывшие в употреблении. Наугад взято три микрокалькулятора. Какова вероятность, что все они окажутся новыми?
ешение.
Рассмотрим события:
А – первый из взятых микрокалькуляторов новый
В – второй микрокалькулятор новый
С – третий микрокалькулятор новый
Тогда Р(А) = 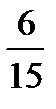
Вероятность того, что второй микрокалькулятор будет новый, при условии, что уже отобраны два новых микрокалькулятора, т.е. условная вероятность события В, равна
РА(В) = 
Вероятность того, что третьим будет отобран новый микрокалькулятор, при условии, что уже отобраны два новых микрокалькулятора, т.е. условная вероятность события С, равна
РАВ (С) = 
Искомая вероятность того, что все три отобранных микрокалькулятора окажутся новыми, равна
Р(АВС) = Р(А) · РА(В) · РАВ (С) = 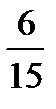 ·
·  ·
·  =
= 
адача 3.
Наборщик типографии использует 2 набора шрифтов одинакового объема, при этом в 1-м из них 80%, а во 2-м – 90% отличного шрифта. Наудачу извлеченная литера из наудачу взятого набора оказалась отличного качества.
Найти вероятность того, что эта литера взята из 2-го набора.
ешение.
Как и в предыдущей задаче, обозначим события 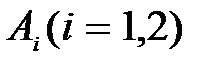 - литера с i -го набора, вероятности этих событий
- литера с i -го набора, вероятности этих событий  Эти события образуют полную группу событий. Событие В – наудачу взятая литера отличного качества. По условию
Эти события образуют полную группу событий. Событие В – наудачу взятая литера отличного качества. По условию 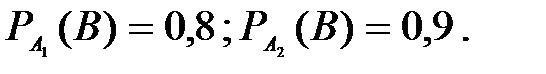
Требуется найти вероятность  , т.е. переоценить вероятность гипотезы А2 , когда событие В уже наступило. Используем формулу Бейеса
, т.е. переоценить вероятность гипотезы А2 , когда событие В уже наступило. Используем формулу Бейеса 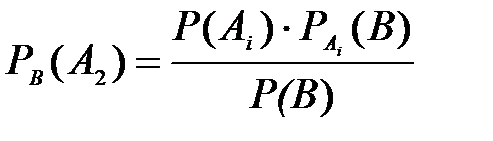 , где
, где  - формула полной вероятности. Получаем искомую вероятность
- формула полной вероятности. Получаем искомую вероятность 

адача 4.
После года хранения на складе в среднем 10% аккумуляторов выходит из строя. Определить вероятность того, что после года хранения из 12 аккумуляторов окажутся годными:
а) 10;
б) больше половины.
ешение.
Событие А – наудачу взятый аккумулятор после года хранения годный. Вероятность 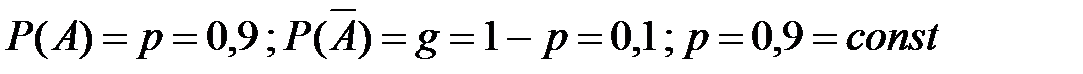 для каждого из n =12 аккумуляторов.
для каждого из n =12 аккумуляторов.
а) Следует определить вероятность  . применим формулу Бернулли:
. применим формулу Бернулли:  .
.
Получаем:  .
.
б) 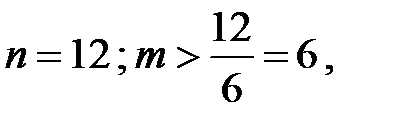 т.е. m = 7, 8, 9, 10, 11, 12.
т.е. m = 7, 8, 9, 10, 11, 12.
Искомая вероятность 
адача 5.
Вероятность изготовления бракованной отливки равна 0,002.
Определить вероятность того, что из выпущенных 500 отливок количество бракованных составит:
а) 2;
б) более двух.
Решение. В этой задаче n = 500 велико, p = 0,002 мала, произведение 
а) m = 2. Найти вероятность P 2,500 можно по формуле Бернулли, но это нецелесообразно ввиду громоздкости вычислений. Воспользуемся формулой Пуассона 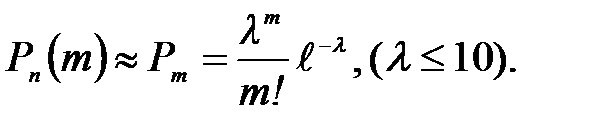
Вероятность находим, пользуясь таблицей значений функции Пуассона: P 2,500 = 0,1839.
б) m >2, т.е. m = 3,4..., 500 P 500(m >2) надо найти.
Перейдем к противоположному событию  , тогда
, тогда  Для вычисления каждого слагаемого
Для вычисления каждого слагаемого  используем формулу Пуассона при
используем формулу Пуассона при  и
и  .
.
Получаем, пользуясь таблицей: 
адача 6.
Вероятность своевременного выполнения заказа цехами службы быта равна 0,75.
Найти вероятность того, что из 160 заказов своевременно выполнят:
а) 120;
б) не менее 110.
ешение.
Вероятность выполнения каждого заказа  невыполнения -
невыполнения - 
а) n =160 велико, m = 120; p близко к 0,5. Для вычисления вероятности  воспользуемся формулой Муавра-Лапласа:
воспользуемся формулой Муавра-Лапласа: 
 .
.
Значения функции Гаусса 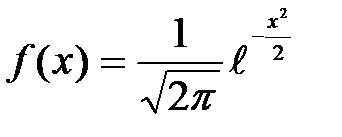 находим по таблице, учитывая ее четность:
находим по таблице, учитывая ее четность:  .
.
Находим: 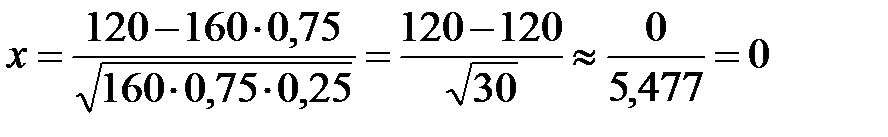 .
.
По таблице находим 
Искомая вероятность 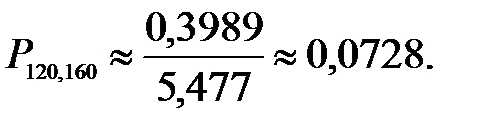
б)  , т.е. надо найти вероятность
, т.е. надо найти вероятность 
Применим интегральную теорему Муавра-Лапласа:  , где
, где  а
а  - функция Лапласа, значения которой табулированы, функция нечетная.
- функция Лапласа, значения которой табулированы, функция нечетная.
Вычисляем:  .
.
По таблице находим: 

Получаем: искомая вероятность: 
адача 7.
Заданы законы распределения двух независимых случайных величин Х и Y
Х -5 2 3 4 Y 1 4
Р 0,4 0,3 0,1 0,2 Р 0,2 0,8
Найти математическое ожидание и дисперсию для случайной величины Z = 2X – 7Y
Решение.
Найдем математическое ожидание и дисперсию для случайных величин Х и Y.
М(Х) = – 5 · 0,4 + 2 · 0,3 + 3 · 0,1 + 4 · 0,2 = – 0,3;
М(Y) = 1· 0,2 + 4 · 0,8 = 3,4
Напишем законы распределения для случайных Х2 и Y2:
Х2 25 4 9 16 Y2 1 16
Р 0,4 0,3 0,1 0,2 Р 0,2 0,8
Найдем математическое ожидание для случайных величин Х2 и Y2:
М(Х2) = 25 · 0,4 + 4 · 0,3 + 9 · 0,1 + 16 · 0,2 = 15,3;
М(Y2) = 1· 0,2 + 16 · 0,8 = 13,0
Отсюда
D(X) = M(X2) – [ M(X)]2 = 15,3 – (– 0,3)2 = 15,21
D(Y) = M(Y2) – [ M(Y)]2 = 13,0 – (3,4)2 = 1,44
Наконец, пользуясь свойствами математического ожидания и дисперсии, а также независимостью случайных величин Х и Y, получаем
М(Z) = M(2X – 7Y) = 2M(X) – 7M(Y) = 2(– 0,3) - 7· 3,4 = – 24,4
D(Z) = D(2X – 7Y) = 4D (X) + 49 · D(Y) = 4 · 15,21 + 49 · 1,44 = 131,4
адача 8.
Случайная величина Х задана функцией распределения вероятностей
0 при х £ -3
F(x) =  (х + 3)2 при –3< x £ 0
(х + 3)2 при –3< x £ 0
1 при х > 0
Найти:
а) вероятность попадания случайной величины Х в интервал  ;
;
б) плотность распределения вероятностей случайной величины Х;
в) математическое ожидание случайной величины Х.
ешение.
а) вероятность того, что случайная величина Х примет значение, заключенное в интервале  , равна приращению функции распределения на этом интервале:
, равна приращению функции распределения на этом интервале:
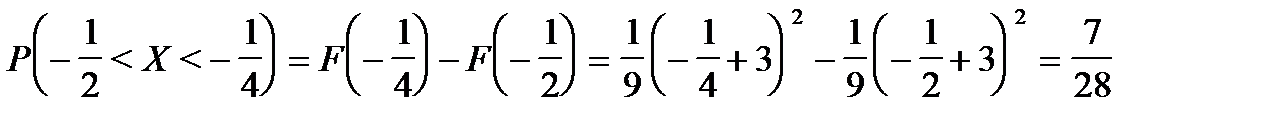
б) Найдем плотность распределения вероятностей случайной величины Х по формуле f (x) = F¢ (x)
Получаем
0 при х £ -3
F(x) = 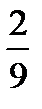 (х + 3)2 при –3< x £ 0
(х + 3)2 при –3< x £ 0
0 при х > 0
в) Математическое ожидание случайной величины Х находим по формуле 
Имеем

Задача 9.
Станок–автомат изготавливает шарики. Шарик считается годным, если отклонение Х его диаметра от проектного размера по абсолютной величине меньше 0,9 мм. Считая, что случайная величина Х распределена нормально с нулевым математическим ожиданием и со средним квадратическим отклонением σ = 0,5 мм, найти, сколько процентов годных шариков изготовляет станок–автомат.
ешение.
Воспользуемся формулой для вычисления вероятности заданного отклонения нормально распределенной случайной величины Х от ее математического ожидания
Р(|Х - α| < ε) = 2Ф 
где α = М(Х), σ2 = D(X), Ф(х) – функция Лапласа (см. приложение 1).
По условию задачи α = М(Х) = 0; σ = 0,5; ε = 0,9, поэтому Р(│Х│<0,9)=2Ф (1,8)=2·0,4641=0,9282
Таким образом, станок–автомат изготавливает 92,8% годных шариков.






