Введём двумерное нормальное распределение случайного вектора 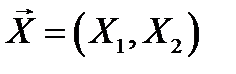 .
.
Пусть координаты  и
и  случайного вектора
случайного вектора 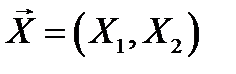 являются случайными величинами, распределёнными по нормальному закону, т.е. имеют плотности распределения
являются случайными величинами, распределёнными по нормальному закону, т.е. имеют плотности распределения 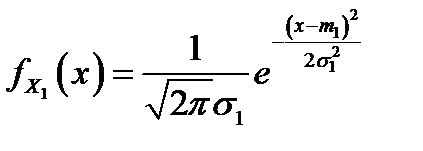 и
и  . Если
. Если  и
и  являются независимыми случайными величинами, то
являются независимыми случайными величинами, то 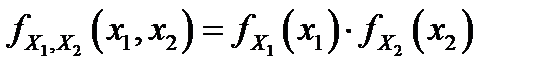 , и в этом случае плотность распределения двумерного нормального распределения имеет вид
, и в этом случае плотность распределения двумерного нормального распределения имеет вид 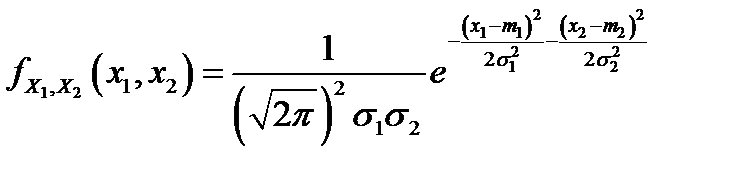 . В общем случае вектор
. В общем случае вектор 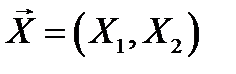 имеет (невырожденное) двумерное нормальное распределение, если его плотность распределения определяется формулой
имеет (невырожденное) двумерное нормальное распределение, если его плотность распределения определяется формулой  , где функция двух переменных
, где функция двух переменных 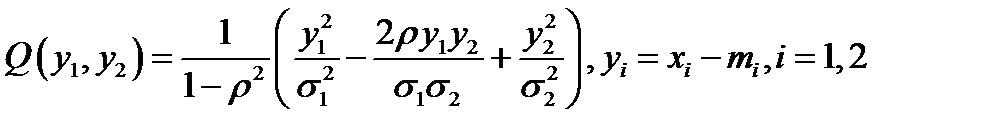 есть положительно определённая квадратичная форма (т.е.
есть положительно определённая квадратичная форма (т.е. 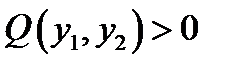 для любых
для любых 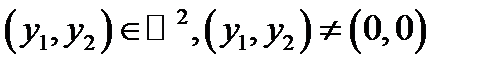 ).
).
Двумерное нормальное распределение зависит от пяти параметров:
– координат  и
и  вектора
вектора  , называемого вектором математических ожиданий вектора
, называемого вектором математических ожиданий вектора 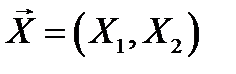 ;
;
– координат 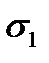 и
и 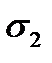 вектора
вектора  , называемого вектором средних квадратических отклонений вектора
, называемого вектором средних квадратических отклонений вектора 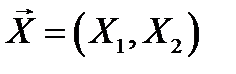 ;
;
– числа  , называемого коэффициентом корреляции случайных величин
, называемого коэффициентом корреляции случайных величин 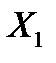 и
и 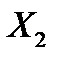 .
.
словные вероятности и плотности вероятностей. Независимость случайных величин.
Условным законом распределения случайной величины, входящей в систему, называется её закон распределения, вычисленный при условии, что другая случайная величина приняла определённое значение.
Условные функции распределения случайных величин  и
и  , входящих в систему, обозначаются
, входящих в систему, обозначаются 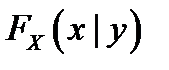 и
и  , а условные плотности распределения –
, а условные плотности распределения –  и
и 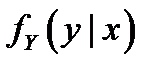 .
.
Теорема умножения плотностей распределения:  или
или 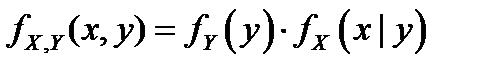 .
.
Для независимых случайных величин 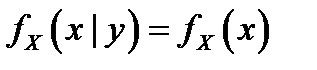 или
или  .
.
 – условная вероятность.
– условная вероятность.
Случайные величины  и
и  называют независимыми, если совместная функция распределения
называют независимыми, если совместная функция распределения  является произведением одномерных функций распределения
является произведением одномерных функций распределения  и
и  :
:  . В противном случае случайные величины называют зависимыми.
. В противном случае случайные величины называют зависимыми.
Для независимых случайных величин  и
и  события
события 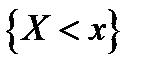 и
и 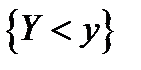 являются независимыми. Покажем, что независимыми являются и все события
являются независимыми. Покажем, что независимыми являются и все события  и
и 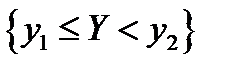 . Действительно, в силу независимости
. Действительно, в силу независимости  и
и  , свойства 5 двумерной функции распределения (
, свойства 5 двумерной функции распределения (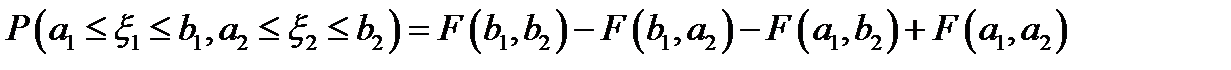 ) и свойства 3 одномерной функции распределения (
) и свойства 3 одномерной функции распределения ( ) имеем
) имеем 

 , что и означает независимость событий
, что и означает независимость событий  и
и 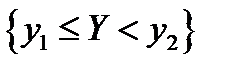 .
.
Теорема: Для того, чтобы непрерывные случайные величины  и
и  были независимыми, необходимо и достаточно, чтобы для всех
были независимыми, необходимо и достаточно, чтобы для всех  и
и 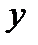
 .
.
Доказательство: I.Необходимость. Пусть случайные величины  и
и  независимы. Тогда, согласно определению
независимы. Тогда, согласно определению  . Имеем:
. Имеем:  .
.
II.Достаточность.. Теорема доказана.
Теорема: Дискретные случайные величины  и
и  являются независимыми тогда и только тогда, когда для всех возможных значений
являются независимыми тогда и только тогда, когда для всех возможных значений  и
и 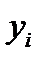
 .
.
Случайные величины  , заданные на одном и том же вероятностном пространстве, называют независимыми в совокупности, если
, заданные на одном и том же вероятностном пространстве, называют независимыми в совокупности, если 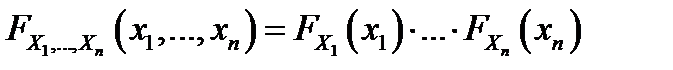 .
.






