Скалярная случайная величина принимает значения из некоторого множества, до опыта заранее не известные.
Примеры случайных величин: количество студентов на занятии, уровень воды в реке, сила электрического тока в сети в конкретный момент времени, количество частиц в пригоршне песка и т.п.
В зависимости от множества принимаемых значений случайные величины подразделяются на непрерывные (НСВ) и дискретные (ДСВ).
У дискретной случайной величины множество значений конечно, либо счётно. Если множество значений несчётно, то случайная величина является непрерывной. Также различают смешанные случайные величины.
Случайные величины обозначаются: 
.
– случайные события, у которых можно считать вероятность.
Малыми латинскими буквами обозначаются конкретные значения случайной величины.
Закон распределения случайной величины: 
. 
– измеримая функция, действующая из 
в подмножество 
пространства 
. – множество значений случайной величины 
.
Измеримость функции 
позволяет любому бореевскому множеству
|
|
|
|
|
|
|
|
поставить в соответствие одно конкретное множество 
из 
. Таким образом 
, поэтому вероятность события 
есть вероятность события 
: 
. Закон распределения – связь между подмножеством значений случайной величины и вероятностью её попадания в это подмножество.
Случайная величина считается заданной, если задан её закон распределения и множество значений.
Вид функции полностью задаёт закон распределения.
Как правило в практических задачах явный вид функции неизвестен. Его либо невозможно, либо крайне трудно найти.
Если 
, то имеем вероятность 
– функция распределения. 
полностью задаёт закон распределения.
Свойства функции распределения:
1. 
;
2. 
;
3. 
Доказательство: 
, ч.т.д.
4. 
;
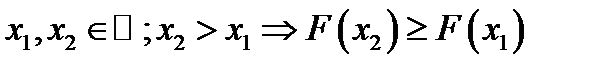5. 
Доказательство: 
, ч.т.д.
искретная случайная величина. Формы задания закона распределения дискретной случайной величины.
Случайную величину 
называют дискретной, если множество её возможных значений конечно или счётно.
Формы задания закона распределения ДСВ:
1. Ряд распределения. 
| 
| 
| 
| 
| 
| 
|
| 
| 
| 
| 
| 
|
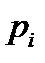
Свойства ряда распределения:
1. 
;
2. 
– свойство нормировки;
3. 
;
4. 
Доказательство: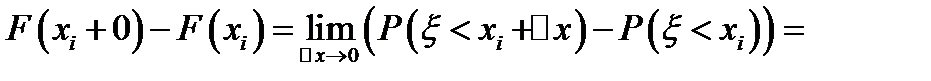 
, ч.т.д.
2. 
Функция распределения. Функция распределения ДСВ является кусочно постоянной функцией, принимающей на промежутке 
значение 0, на промежутках 
– значение 
и на промежутке 
– значение 1.
3. 
Аналитическое и графическое задание закона распределения ДСВ. Для задания закона распределения ДСВ, наряду с рядом распределения и функцией распределения, используют другие способы. Например, распределение игральной кости описывают формулой 
. Графическое изображение этого распределения приведено на рисунке.
