Классическое определение вероятности.
Пусть всего  элементарных исходов,
элементарных исходов,  – число исходов, благоприятствующих событию
– число исходов, благоприятствующих событию  . Тогда
. Тогда 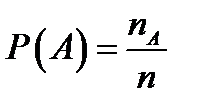 – вероятность.
– вероятность.
1.  – число сочетаний. Если опыт состоит в выборе
– число сочетаний. Если опыт состоит в выборе  элементов из
элементов из  без упорядочения и без возвращения, то общее число элементарных исходов в опыте будет равно количеству различных
без упорядочения и без возвращения, то общее число элементарных исходов в опыте будет равно количеству различных  комбинаций, отличных друг от друга, по крайней мере, одним составом элементов.
комбинаций, отличных друг от друга, по крайней мере, одним составом элементов.
2.  – число размещений без повторений. Если опыт состоит в выборе
– число размещений без повторений. Если опыт состоит в выборе  элементов из
элементов из  без возвращения, но с упорядочением элементов по мере их поступления, то количество элементарных исходов равно числу
без возвращения, но с упорядочением элементов по мере их поступления, то количество элементарных исходов равно числу  комбинаций, отличных друг от друга либо порядком следования элементов, либо их составом (но один и тот же элемент встречается в группе не более одного раза).
комбинаций, отличных друг от друга либо порядком следования элементов, либо их составом (но один и тот же элемент встречается в группе не более одного раза).
3.  – число размещений с повторениями. Если опыт состоит в выборе
– число размещений с повторениями. Если опыт состоит в выборе  элементов из
элементов из  с возвращением и упорядочением элементов по мере их поступления, то общее число исходов опыта равно количеству
с возвращением и упорядочением элементов по мере их поступления, то общее число исходов опыта равно количеству  комбинаций, отличающихся друг от друга составом элементов, либо порядком их следования (при этом один и тот же элемент может повторяться несколько раз).
комбинаций, отличающихся друг от друга составом элементов, либо порядком их следования (при этом один и тот же элемент может повторяться несколько раз).
Геометрическое определение вероятности.
Если множество элементарных исходов может быть представлено некоторой областью  , а множество благоприятствующих событию
, а множество благоприятствующих событию  исходов – подобластью
исходов – подобластью  , то
, то  .
.
Статистическое определение вероятности.
Рассмотрим опыт, в котором событие  может появиться, а может и не появиться, и проведём этот опыт
может появиться, а может и не появиться, и проведём этот опыт  раз. Пусть
раз. Пусть  раз событие
раз событие 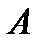 произошло, тогда
произошло, тогда  .
.
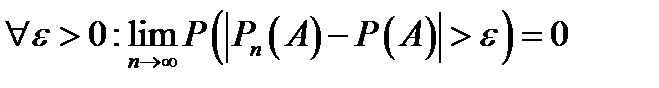 – сходимость по вероятности.
– сходимость по вероятности.
Вероятностью события  называют (эмпирический) предел
называют (эмпирический) предел  , к которому стремится частота
, к которому стремится частота  события
события  при неограниченном увеличении числа
при неограниченном увеличении числа  опытов.
опытов.
еорема сложения. Следствия.
Теорема:  . Для
. Для 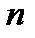 событий:
событий:  .
.

|

|
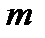
|

|

|
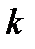
|

|
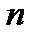 исходов.
исходов.

еорема доказана.
Следствие 1: если  и
и  несовместны, то
несовместны, то  .
.
Следствие 2: 
Доказательство: 
словная вероятность и её свойства. Теорема умножения вероятностей.
Говорят, что событие  зависит от события
зависит от события  , если его вероятность меняется, когда происходит событие
, если его вероятность меняется, когда происходит событие 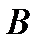 .
.
Условная вероятность – это вероятность события  , подсчитанная при условии, что
, подсчитанная при условии, что  произошло. (
произошло. ( –
– 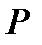 от
от  при условии
при условии  )
)
Если события  и
и  независимы, то
независимы, то  .
.
Теорема:
 Для
Для 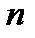 событий:
событий:  .
.

|

|
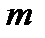
|

|

|
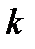
|

|
 исходов.
исходов.  благоприятствуют
благоприятствуют  исходов,
исходов,  благоприятствуют
благоприятствуют  исходов,
исходов,  –
–  исходов. Пусть
исходов. Пусть  произошло, осталось
произошло, осталось 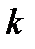 исходов,
исходов,  из них благоприятствуют
из них благоприятствуют  .
.


 . Теорема доказана.
. Теорема доказана.
Следствие 1: если  не зависит от
не зависит от  , то
, то  .
.
Следствие 2: если  зависит от
зависит от  , то
, то  зависит от
зависит от  .
.






